This article describes local normal forms of functions in noncommuting variables, up to equivalence generated by isomorphism of noncommutative Jacobi algebras, extending singularity theory in the style of Arnold’s commutative local normal forms into the noncommutative realm. This generalisation unveils many new phenomena, including an ADE classification when the Jacobi ring has dimension zero and, by taking suitable limits, a further ADE classification in dimension one. These are natural generalisations of the simple singularities and those with infinite multiplicity in Arnold’s classification. We obtain normal forms away from some exceptional Type E cases. Remarkably, these normal forms have no continuous parameters, and the key new feature is that the noncommutative world affords larger families.

This theory has a range of immediate consequences to the birational geometry of 3-folds. The normal forms of dimension zero are the analytic classification of smooth 3-fold flops, and one outcome of NC singularity theory is the first list of all Type D flopping germs, generalising Reid’s famous pagoda classification of Type A, with variants covering Type E. The normal forms of dimension one have further applications to divisorial contractions to a curve. In addition, the general techniques also give strong evidence towards new contractibility criteria for rational curves.

Given any smooth germ of a 3-fold flopping contraction, we first give a combinatorial characterisation of which Gopakumar–Vafa (GV) invariants are non-zero, by prescribing multiplicities to the walls in the movable cone. On the Gromov–Witten (GW) side, this allows us to describe, and even draw, the critical locus of the associated quantum potential. We prove that the critical locus is the infinite hyperplane arrangement of Iyama and the second author and, moreover, that the quantum potential can be reconstructed from a finite fundamental domain. We then iterate, obtaining a combinatorial description of the matrix that controls the transformation of the non-zero GV invariants under a flop. There are three main ingredients and applications: (1) a construction of flops from simultaneous resolution via cosets, which describes how the dual graph changes; (2) a closed formula, which describes the change in dimension of the contraction algebra under flop; and (3) a direct and explicit isomorphism between quantum cohomologies of different crepant resolutions, giving a Coxeter-style, visual proof of the Crepant Transformation Conjecture for isolated cDV singularities.

A twisting system is one of the major tools to study graded algebras; however, it is often difficult to construct a (nonalgebraic) twisting system if a graded algebra is given by generators and relations. In this paper, we show that a twisted algebra of a geometric algebra is determined by a certain automorphism of its point variety. As an application, we classify twisted algebras of three-dimensional geometric Artin–Schelter regular algebras up to graded algebra isomorphism.

We formulate a strengthening of the Zariski dense orbit conjecture for birational maps of dynamical degree one. So, given a quasiprojective variety X defined over an algebraically closed field K of characteristic 0$0$ , endowed with a birational self-map \phi $\phi$ of dynamical degree 1$1$ , we expect that either there exists a nonconstant rational function f:X\dashrightarrow \mathbb {P} ^1$f:X\dashrightarrow \mathbb {P} ^1$ such that f\circ \phi =f$f\circ \phi =f$ , or there exists a proper subvariety Y\subset X$Y\subset X$ with the property that, for any invariant proper subvariety Z\subset X$Z\subset X$ , we have that Z\subseteq Y$Z\subseteq Y$ . We prove our conjecture for automorphisms \phi $\phi$ of dynamical degree 1$1$ of semiabelian varieties X. Moreover, we prove a related result for regular dominant self-maps \phi $\phi$ of semiabelian varieties X: assuming that \phi $\phi$ does not preserve a nonconstant rational function, we have that the dynamical degree of \phi $\phi$ is larger than 1$1$ if and only if the union of all \phi $\phi$ -invariant proper subvarieties of X is Zariski dense. We give applications of our results to representation-theoretic questions about twisted homogeneous coordinate rings associated with abelian varieties.

Given a negatively graded Calabi-Yau algebra, we regard it as a DG algebra with vanishing differentials and study its cluster category. We show that this DG algebra is sign-twisted Calabi-Yau and realise its cluster category as a triangulated hull of an orbit category of a derived category and as the singularity category of a finite-dimensional Iwanaga-Gorenstein algebra. Along the way, we give two results that stand on their own. First, we show that the derived category of coherent sheaves over a Calabi-Yau algebra has a natural cluster tilting subcategory whose dimension is determined by the Calabi-Yau dimension and the a-invariant of the algebra. Second, we prove that two DG orbit categories obtained from a DG endofunctor and its homotopy inverse are quasi-equivalent. As an application, we show that the higher cluster category of a higher representation infinite algebra is triangle equivalent to the singularity category of an Iwanaga-Gorenstein algebra, which is explicitly described. Also, we demonstrate that our results generalise the context of Keller–Murfet–Van den Bergh on the derived orbit category involving a square root of the AR translation.

This is a general study of twisted Calabi–Yau algebras that are \mathbb {N}$\mathbb {N}$ -graded and locally finite-dimensional, with the following major results. We prove that a locally finite graded algebra is twisted Calabi–Yau if and only if it is separable modulo its graded radical and satisfies one of several suitable generalizations of the Artin–Schelter regularity property, adapted from the work of Martinez-Villa as well as Minamoto and Mori. We characterize twisted Calabi–Yau algebras of dimension 0 as separable k-algebras, and we similarly characterize graded twisted Calabi–Yau algebras of dimension 1 as tensor algebras of certain invertible bimodules over separable algebras. Finally, we prove that a graded twisted Calabi–Yau algebra of dimension 2 is noetherian if and only if it has finite GK dimension.

The elliptic algebras in the title are connected graded \mathbb {C}$\mathbb {C}$-algebras, denoted 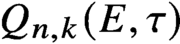Q_{n,k}(E,\tau )$Q_{n,k}(E,\tau )$, depending on a pair of relatively prime integers 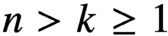n>k\ge 1$n>k\ge 1$, an elliptic curve E and a point 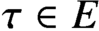\tau \in E$\tau \in E$. This paper examines a canonical homomorphism from 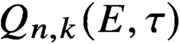Q_{n,k}(E,\tau )$Q_{n,k}(E,\tau )$ to the twisted homogeneous coordinate ring 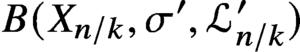B(X_{n/k},\sigma ',\mathcal {L}^{\prime }_{n/k})$B(X_{n/k},\sigma ',\mathcal {L}^{\prime }_{n/k})$ on the characteristic variety 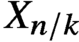X_{n/k}$X_{n/k}$ for 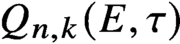Q_{n,k}(E,\tau )$Q_{n,k}(E,\tau )$. When 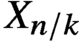X_{n/k}$X_{n/k}$ is isomorphic to 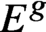E^g$E^g$ or the symmetric power 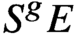S^gE$S^gE$, we show that the homomorphism 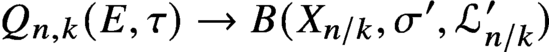Q_{n,k}(E,\tau ) \to B(X_{n/k},\sigma ',\mathcal {L}^{\prime }_{n/k})$Q_{n,k}(E,\tau ) \to B(X_{n/k},\sigma ',\mathcal {L}^{\prime }_{n/k})$ is surjective, the relations for 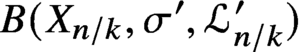B(X_{n/k},\sigma ',\mathcal {L}^{\prime }_{n/k})$B(X_{n/k},\sigma ',\mathcal {L}^{\prime }_{n/k})$ are generated in degrees 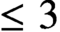\le 3$\le 3$ and the noncommutative scheme 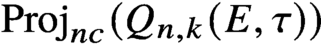\mathrm {Proj}_{nc}(Q_{n,k}(E,\tau ))$\mathrm {Proj}_{nc}(Q_{n,k}(E,\tau ))$ has a closed subvariety that is isomorphic to 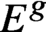E^g$E^g$ or 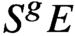S^gE$S^gE$, respectively. When 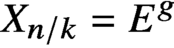X_{n/k}=E^g$X_{n/k}=E^g$ and 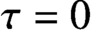\tau =0$\tau =0$, the results about 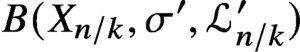B(X_{n/k},\sigma ',\mathcal {L}^{\prime }_{n/k})$B(X_{n/k},\sigma ',\mathcal {L}^{\prime }_{n/k})$ show that the morphism 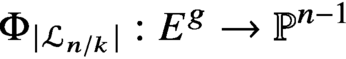\Phi _{|\mathcal {L}_{n/k}|}:E^g \to \mathbb {P}^{n-1}$\Phi _{|\mathcal {L}_{n/k}|}:E^g \to \mathbb {P}^{n-1}$ embeds 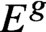E^g$E^g$ as a projectively normal subvariety that is a scheme-theoretic intersection of quadric and cubic hypersurfaces.

Generalised quantum determinantal rings are the analogue in quantum matrices of Schubert varieties. Maximal orders are the noncommutative version of integrally closed rings. In this paper, we show that generalised quantum determinantal rings are maximal orders. The cornerstone of the proof is a description of generalised quantum determinantal rings, up to a localisation, as skew polynomial extensions.

We study Van den Bergh's non-commutative symmetric algebra 𝕊nc(M) (over division rings) via Minamoto's theory of Fano algebras. In particular, we show that 𝕊nc(M) is coherent, and its proj category ℙnc(M) is derived equivalent to the corresponding bimodule species. This generalizes the main theorem of [8], which in turn is a generalization of Beilinson's derived equivalence. As corollaries, we show that ℙnc(M) is hereditary and there is a structure theorem for sheaves on ℙnc(M) analogous to that for ℙ1.

We study the structure of the stable category \text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$ of graded maximal Cohen–Macaulay module over S/(f)$S/(f)$ where S$S$ is a graded (\pm 1$\pm 1$)-skew polynomial algebra in n$n$ variables of degree 1, and f=x_{1}^{2}+\cdots +x_{n}^{2}$f=x_{1}^{2}+\cdots +x_{n}^{2}$. If S$S$ is commutative, then the structure of \text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$ is well known by Knörrer’s periodicity theorem. In this paper, we prove that if n\leqslant 5$n\leqslant 5$, then the structure of \text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$ is determined by the number of irreducible components of the point scheme of S$S$ which are isomorphic to \mathbb{P}^{1}$\mathbb{P}^{1}$.

We introduce the notion of exact tilting objects, which are partial tilting objects T$T$ inducing an equivalence between the abelian category generated by T$T$ and the category of modules over the endomorphism algebra of T$T$. Given a chain of sufficiently negative rational curves on a rational surface, we construct an exceptional sequence whose universal extension is an exact tilting object. For a chain of (-2)$(-2)$-curves, we obtain an equivalence with modules over a well-known algebra.

In this paper we consider Grassmannians in arbitrary characteristic. Generalizing Kapranov’s well-known characteristic-zero results, we construct dual exceptional collections on them (which are, however, not strong) as well as a tilting bundle. We show that this tilting bundle has a quasi-hereditary endomorphism ring and we identify the standard, costandard, projective and simple modules of the latter.

Classification of AS-regular algebras is one of the major projects in non-commutative algebraic geometry. In this paper, we will study when given AS-regular algebras are graded Morita equivalent. In particular, for every geometric AS-regular algebra A, we define another graded algebra A, and show that if two geometric AS-regular algebras A and A' are graded Morita equivalent, then A and A' are isomorphic as graded algebras. We also show that the converse holds in many three-dimensional cases. As applications, we apply our results to Frobenius Koszul algebras and Beilinson algebras.

Dimer models are a combinatorial tool to describe certain algebras that appear as noncommutative crepant resolutions of toric Gorenstein singularities. Unfortunately, not every dimer model gives rise to a noncommutative crepant resolution. Several notions of consistency have been introduced to deal with this problem. In this paper, we study the major different notions in detail and show that for dimer models on a torus, they are all equivalent.

We generalise statements known about Springer fibres associated to nilpotents with two Jordan blocks to Spaltenstein varieties. We study the geometry of generalised irreducible components (i.e. Bialynicki-Birula cells) and their pairwise intersections. In particular, we develop a graphical calculus that encodes their structure as iterated fibre bundles with ℂℙ1 as base spaces, and compute their cohomology. At the end, we present a connection with coloured cobordisms generalising the construction of Khovanov (M. Khovanov, A categorification of the Jones polynomial, Duke Math. J. 101(3) (2000), 359–426) and Stroppel (C. Stroppel, Parabolic category O, perverse sheaves on Grassmannians, Springer fibres and Khovanov homology, Compositio Mathematica145(4) (2009), 954–992).

We study quantum Schubert varieties from the point of view of regularity conditions. More precisely, we show that these rings are domains that are maximal orders and are AS-Cohen-Macaulay and we determine which of them are AS-Gorenstein. One key fact that enables us to prove these results is that quantum Schubert varieties are quantum graded algebras with a straightening law that have a unique minimal element in the defining poset. We prove a general result showing when such quantum graded algebras are maximal orders. Finally, we exploit these results to show that quantum determinantal rings are maximal orders.

Let $A$ be a graded algebra finitely generated in degree 1 over a field $k$. Point modules over $A$ introduced by Artin, Tate and Van den Bergh play an important role in studying $A$ in noncommutative algebraic geometry. In this paper, we define a dual notion of point module in terms of Koszul duality, which we call a co-point module. Using co-point modules, we will construct counter-examples to the following condition due to Auslander: for every finitely generated right module $\pi$ over a ring $R$, there is a natural number $n_M\in {\mathbb N}$ such that, for any finitely generated right module $N$ over $R$, ${\rm Ext}^i_R(M, N)=0$ for all $i\gg 0$ implies ${\rm Ext}^i_R(M, N)=0$ for all $i>n_M$.

We prove a general theorem showing that iterated skew polynomial extensions of the type that fit the conditions needed by Cauchon's deleting derivations theory and by the Goodearl–Letzter stratification theory are unique factorisation rings in the sense of Chatters and Jordan. This general result applies to many quantum algebras; in particular, generic quantum matrices and quantized enveloping algebras of the nilpotent part of a semisimple Lie algebra are unique factorisation domains in the sense of Chatters. The result also extends to generic quantum grassmannians (by using noncommutative dehomogenisation) and to the quantum groups ${\mathcal O}_q(\text{GL}_n)$ and ${\mathcal O}_q(\text{SL}_n)$.

Let $Y \rightrightarrows X$ be a finite flat groupoid scheme with $X$ a quasi-projective variety and let $S$ be its coarse moduli scheme. We associate to the groupoid scheme a coherent sheaf of algebras $\mathcal{O}_{X / Y}$ on $S$ which we call the non-commutative coordinate ring of the groupoid scheme. We show that when $X$ is a smooth curve and the groupoid action is generically free, the non-commutative coordinate rings which can occur are, up to Morita equivalence, the hereditary orders on smooth curves. This gives a bijective correspondence between smooth one-dimensional Deligne–Mumford stacks of finite type and Morita equivalence classes of hereditary orders on smooth curves.

This paper introduces baby Verma modules for symplectic reflection algebras of complex reflection groups at parameter $t=0$ (the so-called rational Cherednik algebras at parameter $t=0$), and presents their most basic properties. Baby Verma modules are then used to answer several problems posed by Etingof and Ginzburg, and to give an elementary proof of a theorem of Finkelberg and Ginzburg.