Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T17:14:58.252Z Has data issue: false hasContentIssue false
  • English
  • Français

On Knörrer Periodicity for Quadric Hypersurfaces in Skew Projective Spaces

Part of: Representation theory of rings and algebras Rings and algebras arising under various constructions Abelian categories Algebraic geometry: Foundations

Published online by Cambridge University Press:  03 December 2018

Kenta Ueyama
Kenta Ueyama*
Affiliation:
Department of Mathematics, Faculty of Education, Hirosaki University, 1 Bunkyocho, Hirosaki, Aomori 036-8560, Japan Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the structure of the stable category 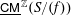$\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$ of graded maximal Cohen–Macaulay module over 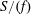$S/(f)$ where 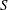$S$ is a graded (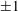$\pm 1$)-skew polynomial algebra in $n$ variables of degree 1, and 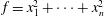$f=x_{1}^{2}+\cdots +x_{n}^{2}$. If 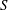$S$ is commutative, then the structure of 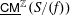$\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$ is well known by Knörrer’s periodicity theorem. In this paper, we prove that if 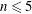$n\leqslant 5$, then the structure of 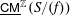$\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$ is determined by the number of irreducible components of the point scheme of 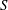$S$ which are isomorphic to 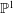$\mathbb{P}^{1}$.

Keywords

Knörrer periodicitystable categorynoncommutative quadric hypersurfaceskew polynomial algebrapoint scheme

MSC classification

Primary: 16G50: Cohen-Macaulay modules
Secondary: 16S38: Rings arising from non-commutative algebraic geometry 18E30: Derived categories, triangulated categories 14A22: Noncommutative algebraic geometry
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 4 , December 2019 , pp. 896 - 911
Copyright
© Canadian Mathematical Society 2018 

Footnotes

The author was supported by JSPS Grant-in-Aid for Early-Career Scientists 18K13381.

References

Artin, M., Tate, J., and Van den Bergh, M., Some algebras associated to automorphisms of elliptic curves . In: The Grothendieck Festschrift, vol. I , Prog. Math., 86, Birkhäuser, Boston, MA, 1990, pp. 33–85.Google Scholar
Belmans, P., De Laet, K., and Le Bruyn, L., The point variety of quantum polynomial rings . J. Algebra 463(2016), 10–22. https://doi.org/10.1016/j.jalgebra.2016.06.013 Google Scholar
Buchweitz, R.-O., Eisenbud, D., and Herzog, J., Cohen–Macaulay modules on quadrics . In: Singularities, representation of algebras, and vector bundles (Lambrecht, 1985) , Lecture Notes in Math., 1273, Springer, Berlin, 1987, pp. 58–116. https://doi.org/10.1007/BFb0078838 Google Scholar
Jørgensen, P., Local cohomology for non-commutative graded algebras . Comm. Algebra 25(1997), no. 2, 575–591. https://doi.org/10.1080/00927879708825875 Google Scholar
Knörrer, H., Cohen–Macaulay modules on hypersurface singularities. I . Invent. Math. 88(1987), 153–164. https://doi.org/10.1007/BF01405095 Google Scholar
Mori, I., Co-point modules over Koszul algebras . J. London Math. Soc. (2) 74(2006), no. 3, 639–656. https://doi.org/10.1112/S002461070602326X Google Scholar
Smith, S. P., Some finite-dimensional algebras related to elliptic curves . In: Representation theory of algebras and related topics (Mexico City, 1994) , CMS Conf. Proc., 19, Amer. Math. Soc., Providence, RI, 1996, pp. 315–348.Google Scholar
Smith, S. P. and Van den Bergh, M., Noncommutative quadric surfaces . J. Noncommut. Geom. 7(2013), no. 3, 817–856. https://doi.org/10.4171/JNCG/136 Google Scholar
Vitoria, J., Equivalences for noncommutative projective spaces. 2011. arxiv:1001.4400v3 Google Scholar