Let 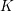 $K$ be a number field. For any system of semisimple mod
$K$ be a number field. For any system of semisimple mod 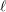 $\ell$ Galois representations
$\ell$ Galois representations 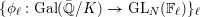 $\{{\it\phi}_{\ell }:\text{Gal}(\bar{\mathbb{Q}}/K)\rightarrow \text{GL}_{N}(\mathbb{F}_{\ell })\}_{\ell }$ arising from étale cohomology (Definition 1), there exists a finite normal extension
$\{{\it\phi}_{\ell }:\text{Gal}(\bar{\mathbb{Q}}/K)\rightarrow \text{GL}_{N}(\mathbb{F}_{\ell })\}_{\ell }$ arising from étale cohomology (Definition 1), there exists a finite normal extension 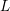 $L$ of
$L$ of 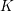 $K$ such that if we denote
$K$ such that if we denote 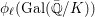 ${\it\phi}_{\ell }(\text{Gal}(\bar{\mathbb{Q}}/K))$ and
${\it\phi}_{\ell }(\text{Gal}(\bar{\mathbb{Q}}/K))$ and 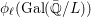 ${\it\phi}_{\ell }(\text{Gal}(\bar{\mathbb{Q}}/L))$ by
${\it\phi}_{\ell }(\text{Gal}(\bar{\mathbb{Q}}/L))$ by 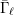 $\bar{{\rm\Gamma}}_{\ell }$ and
$\bar{{\rm\Gamma}}_{\ell }$ and 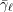 $\bar{{\it\gamma}}_{\ell }$, respectively, for all
$\bar{{\it\gamma}}_{\ell }$, respectively, for all 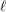 $\ell$ and let
$\ell$ and let 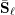 $\bar{\mathbf{S}}_{\ell }$ be the
$\bar{\mathbf{S}}_{\ell }$ be the 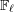 $\mathbb{F}_{\ell }$-semisimple subgroup of
$\mathbb{F}_{\ell }$-semisimple subgroup of 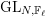 $\text{GL}_{N,\mathbb{F}_{\ell }}$ associated to
$\text{GL}_{N,\mathbb{F}_{\ell }}$ associated to 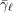 $\bar{{\it\gamma}}_{\ell }$ (or
$\bar{{\it\gamma}}_{\ell }$ (or 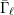 $\bar{{\rm\Gamma}}_{\ell }$) by Nori’s theory [On subgroups of
$\bar{{\rm\Gamma}}_{\ell }$) by Nori’s theory [On subgroups of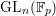 $\text{GL}_{n}(\mathbb{F}_{p})$, Invent. Math. 88 (1987), 257–275] for sufficiently large
$\text{GL}_{n}(\mathbb{F}_{p})$, Invent. Math. 88 (1987), 257–275] for sufficiently large 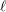 $\ell$, then the following statements hold for all sufficiently large
$\ell$, then the following statements hold for all sufficiently large 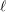 $\ell$.
$\ell$.
A(i) The formal character of 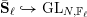 $\bar{\mathbf{S}}_{\ell }{\hookrightarrow}\text{GL}_{N,\mathbb{F}_{\ell }}$ (Definition 1) is independent of
$\bar{\mathbf{S}}_{\ell }{\hookrightarrow}\text{GL}_{N,\mathbb{F}_{\ell }}$ (Definition 1) is independent of 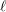 $\ell$ and equal to the formal character of
$\ell$ and equal to the formal character of 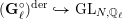 $(\mathbf{G}_{\ell }^{\circ })^{\text{der}}{\hookrightarrow}\text{GL}_{N,\mathbb{Q}_{\ell }}$, where
$(\mathbf{G}_{\ell }^{\circ })^{\text{der}}{\hookrightarrow}\text{GL}_{N,\mathbb{Q}_{\ell }}$, where 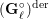 $(\mathbf{G}_{\ell }^{\circ })^{\text{der}}$ is the derived group of the identity component of
$(\mathbf{G}_{\ell }^{\circ })^{\text{der}}$ is the derived group of the identity component of 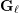 $\mathbf{G}_{\ell }$, the monodromy group of the corresponding semi-simplified
$\mathbf{G}_{\ell }$, the monodromy group of the corresponding semi-simplified 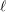 $\ell$-adic Galois representation
$\ell$-adic Galois representation 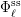 ${\rm\Phi}_{\ell }^{\text{ss}}$.
${\rm\Phi}_{\ell }^{\text{ss}}$.
A(ii) The non-cyclic composition factors of 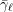 $\bar{{\it\gamma}}_{\ell }$ and
$\bar{{\it\gamma}}_{\ell }$ and 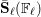 $\bar{\mathbf{S}}_{\ell }(\mathbb{F}_{\ell })$ are identical. Therefore, the composition factors of
$\bar{\mathbf{S}}_{\ell }(\mathbb{F}_{\ell })$ are identical. Therefore, the composition factors of 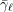 $\bar{{\it\gamma}}_{\ell }$ are finite simple groups of Lie type of characteristic
$\bar{{\it\gamma}}_{\ell }$ are finite simple groups of Lie type of characteristic 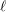 $\ell$ and are cyclic groups.
$\ell$ and are cyclic groups.
B(i) The total 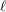 $\ell$-rank
$\ell$-rank 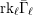 $\text{rk}_{\ell }\bar{{\rm\Gamma}}_{\ell }$ of
$\text{rk}_{\ell }\bar{{\rm\Gamma}}_{\ell }$ of 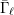 $\bar{{\rm\Gamma}}_{\ell }$ (Definition 14) is equal to the rank of
$\bar{{\rm\Gamma}}_{\ell }$ (Definition 14) is equal to the rank of 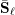 $\bar{\mathbf{S}}_{\ell }$ and is therefore independent of
$\bar{\mathbf{S}}_{\ell }$ and is therefore independent of 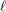 $\ell$.
$\ell$.
B(ii) The 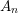 $A_{n}$-type
$A_{n}$-type 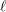 $\ell$-rank
$\ell$-rank 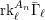 $\text{rk}_{\ell }^{A_{n}}\bar{{\rm\Gamma}}_{\ell }$ of
$\text{rk}_{\ell }^{A_{n}}\bar{{\rm\Gamma}}_{\ell }$ of 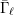 $\bar{{\rm\Gamma}}_{\ell }$ (Definition 14) for
$\bar{{\rm\Gamma}}_{\ell }$ (Definition 14) for 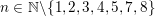 $n\in \mathbb{N}\setminus \{1,2,3,4,5,7,8\}$ and the parity of
$n\in \mathbb{N}\setminus \{1,2,3,4,5,7,8\}$ and the parity of 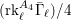 $(\text{rk}_{\ell }^{A_{4}}\bar{{\rm\Gamma}}_{\ell })/4$ are independent of
$(\text{rk}_{\ell }^{A_{4}}\bar{{\rm\Gamma}}_{\ell })/4$ are independent of 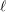 $\ell$.
$\ell$.
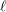 $\ell$-independence for compatible systems of (mod
$\ell$-independence for compatible systems of (mod 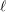 $\ell$) representations
$\ell$) representations
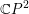 $\mathbb{C}P^{2}$
$\mathbb{C}P^{2}$