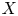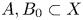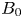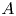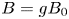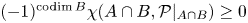Volume 161 - Issue 1 - January 2025
Research Article
Full Poissonian local statistics of slowly growing sequences
- Part of:
-
- Published online by Cambridge University Press:
- 24 March 2025, pp. 148-180
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chai's conjecture for semiabelian Jacobians
- Part of:
-
- Published online by Cambridge University Press:
- 24 March 2025, pp. 120-147
-
- Article
- Export citation
Restriction of p-adic representations of GL2(Qp) to parahoric subgroups
- Part of:
-
- Published online by Cambridge University Press:
- 24 March 2025, pp. 74-119
-
- Article
- Export citation
A nonabelian Fourier transform for tempered unipotent representations
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2025, pp. 13-73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new generic vanishing theorem on homogeneous varieties and the positivity conjecture for triple intersections of Schubert cells
- Part of:
-
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-12
-
- Article
- Export citation