Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T15:13:22.591Z Has data issue: false hasContentIssue false
  • English
  • Français

Spherical subgroups in simple algebraic groups

Part of: Algebraic groups Linear algebraic groups and related topics Special varieties

Published online by Cambridge University Press:  13 February 2015

Friedrich Knop  and
Gerhard Röhrle
Friedrich Knop
Affiliation:
Department Mathematik, Emmy-Noether-Zentrum, FAU Erlangen-Nürnberg, Cauerstrasse 11, 91058 Erlangen, Germany email [email protected]
Gerhard Röhrle
Affiliation:
Fakultät für Mathematik, Ruhr-Universität Bochum, D-44780 Bochum, Germany email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 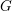$G$ be a simple algebraic group. A closed subgroup 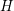$H$ of 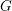$G$ is said to be spherical if it has a dense orbit on the flag variety 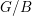$G/B$ of 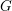$G$. Reductive spherical subgroups of simple Lie groups were classified by Krämer in 1979. In 1997, Brundan showed that each example from Krämer’s list also gives rise to a spherical subgroup in the corresponding simple algebraic group in any positive characteristic. Nevertheless, up to now there has been no classification of all such instances in positive characteristic. The goal of this paper is to complete this classification. It turns out that there is only one additional instance (up to isogeny) in characteristic 2 which has no counterpart in Krämer’s classification. As one of our key tools, we prove a general deformation result for subgroup schemes that allows us to deduce the sphericality of subgroups in positive characteristic from the same property for subgroups in characteristic zero.

Keywords

spherical subgroupsymmetric subgroupspherical homogeneous variety

MSC classification

Primary: 20G15: Linear algebraic groups over arbitrary fields 14M27: Compactifications; symmetric and spherical varieties 14M17: Homogeneous spaces and generalizations
Secondary: 20G05: Representation theory 14L30: Group actions on varieties or schemes (quotients)
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 7 , July 2015 , pp. 1288 - 1308
Copyright
© The Authors 2015 

References

Anantharaman, S., Schémas en groupes, espaces homogènes et espaces algébriques sur une base de dimension 1, Bull. Soc. Math. France, Mem. 33 (1973), 5–79.Google Scholar
Bate, M., Martin, B. and Röhrle, G., A geometric approach to complete reducibility, Invent. Math. 161 (2005), 177–218.CrossRefGoogle Scholar
Bate, M., Martin, B., Röhrle, G. and Tange, R., Closed orbits and uniform S-instability in geometric invariant theory, Trans. Amer. Math. Soc. 365 (2013), 3643–3673.Google Scholar
Bourbaki, N., Éléments de mathématique. Fasc. XXXIV. Groupes et algèbres de Lie. Chapitre IV: Groupes de Coxeter et systèmes de Tits. Chapitre V: Groupes engendrés par des réflexions. Chapitre VI: Systèmes de racines, Actualités Scientifiques et Industrielles, vol. 1337 (Hermann, Paris, 1968).Google Scholar
Bravi, P. and Pezzini, G., Primitive wonderful varieties, Preprint (2011), arXiv:1106.3187.Google Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local: II. Schémas en groupes. Existence d’une donnée radicielle valuée, Publ. Math. Inst. Hautes Études Sci. 60 (1984), 197–376.CrossRefGoogle Scholar
Brundan, J., Dense orbits and double cosets, in Algebraic groups and their representations (Cambridge, 1997), NATO Advanced Study Institutes Series C: Mathematical and Physical Sciences, vol. 517 (Kluwer, Dordrecht, 1998), 259–274.CrossRefGoogle Scholar
Cline, E., Parshall, B. and Scott, L., Cohomology of finite groups of Lie type. I, Publ. Math. Inst. Hautes Études Sci. 45 (1975), 169–191.CrossRefGoogle Scholar
Cline, E., Parshall, B., Scott, L. and van der Kallen, W., Rational and generic cohomology, Invent. Math. 39 (1977), 143–163.CrossRefGoogle Scholar
Duckworth, W. E., Infiniteness of double coset collections in algebraic groups, J. Algebra 273 (2004), 718–733.CrossRefGoogle Scholar
Franjou, V. and van der Kallen, W., Power reductivity over an arbitrary base, Doc. Math., Extra Vol. (2010), 171–195.Google Scholar
Goodman, R. and Wallach, N., Symmetry, representations, and invariants, Graduate Texts in Mathematics, vol. 255 (Springer, Dordrecht, 2009).CrossRefGoogle Scholar
Guralnick, R. M., Liebeck, M. W., Macpherson, D. and Seitz, G. M., Modules for algebraic groups with finitely many orbits on subspaces, J. Algebra 196 (1997), 211–250.CrossRefGoogle Scholar
Jantzen, J. C., Representations of algebraic groups, Mathematical Surveys and Monographs, vol. 107, second edition (American Mathematical Society, Providence, RI, 2003).Google Scholar
Knop, F., Über invariante Bewertungen, welche unter einer reduktiven Gruppe invariant sind, Math. Ann. 295 (1993), 333–363.CrossRefGoogle Scholar
Knop, F., On the set of orbits for a Borel subgroup, Comment. Math. Helv. 70 (1995), 285–309.CrossRefGoogle Scholar
Knop, F., Spherical roots of spherical varieties, Ann. Inst. Fourier (Grenoble) 64 (2014), 2503–2526.CrossRefGoogle Scholar
Krämer, M., Sphärische Untergruppen in kompakten zusammenhängenden Liegruppen, Compositio Math. 38 (1979), 129–153.Google Scholar
Liebeck, M. and Seitz, G., The maximal subgroups of positive dimension in exceptional algebraic groups, Mem. Amer. Math. Soc. 802 (2004), 1–227.Google Scholar
Lübeck, F., Small degree representations of finite Chevalley groups in defining characteristic, LMS J. Comput. Math. 4 (2001), 135–169.CrossRefGoogle Scholar
Richardson, R. W., Conjugacy classes of n-tuples in Lie algebras and algebraic groups, Duke Math. J. 57 (1988), 1–35.CrossRefGoogle Scholar
Rosenlicht, M., Some basic theorems on algebraic groups, Amer. J. Math. 78 (1956), 401–443.CrossRefGoogle Scholar
Demazure, M. and Grothendieck, A. (eds), Schémas en groupes, inSéminaire de Géométrie Algébrique de l’Institut des Hautes Études Scientifiques, 1963 (SGA3), deuxième édition (Institut des Hautes Études Scientifiques, Paris, 1963/1964). (Revised versions appeared as Lecture Notes in Mathematics, vol. 151–153 (Springer) and Doc. Math., vol. 7–8.)Google Scholar
Seitz, G., Double cosets in algebraic groups, in Algebraic groups and their representations (Cambridge, 1997), NATO Advanced Study Institutes Series C: Mathematical and Physical Sciences, vol. 517 (Kluwer, Dordrecht, 1998), 241–257.CrossRefGoogle Scholar
Serre, J.-P., Complète réductibilité, Astérisque 299 (2005), 195–217; Séminaire Bourbaki, Vol. 2003/2004, Exp. No. 932.Google Scholar
Seshadri, C. S., Geometric reductivity over arbitrary base, Adv. Math. 3 (1977), 225–274.CrossRefGoogle Scholar
Springer, T. A., Some results on algebraic groups with involutions, in Algebraic groups and related topics, Advanced Studies in Pure Mathematics, vol. 6 (North-Holland, Amsterdam, 1985), 525–543.CrossRefGoogle Scholar
Springer, T. A., Linear algebraic groups, Progress in Mathematics, vol. 9, second edition (Birkhäuser, Boston, 1998).CrossRefGoogle Scholar
Sumihiro, H., Equivariant completion. II, Kyoto J. Math. 15 (1975), 573–605.CrossRefGoogle Scholar
Thomason, R. W., Equivariant resolution, linearization, and Hilbert’s fourteenth problem over arbitrary base schemes, Adv. Math. 65 (1987), 16–34.CrossRefGoogle Scholar