Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T07:05:29.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Maps from Feigin and Odesskii's elliptic algebras to twisted homogeneous coordinate rings

Part of: Rings and algebras with additional structure Algebraic geometry: Foundations Curves Rings and algebras arising under various constructions

Published online by Cambridge University Press:  11 January 2021

Alex Chirvasitu ,
Ryo Kanda Open the ORCID record for Ryo Kanda [Opens in a new window]  and
S. Paul Smith
Alex Chirvasitu
Affiliation:
Department of Mathematics, University at Buffalo, Buffalo, NY14260-2900, USA; E-mail: [email protected].
Ryo Kanda
Affiliation:
Department of Mathematics, Graduate School of Science, Osaka City University, 3-3-138, Sugimoto, Sumiyoshi, Osaka, 558-8585, Japan; E-mail: [email protected].
S. Paul Smith
Affiliation:
Department of Mathematics, Box 354350, University of Washington, Seattle, WA98195, USA; E-mail: [email protected].

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The elliptic algebras in the title are connected graded $\mathbb {C}$-algebras, denoted 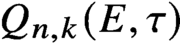$Q_{n,k}(E,\tau )$, depending on a pair of relatively prime integers 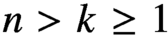$n>k\ge 1$, an elliptic curve E and a point 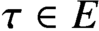$\tau \in E$. This paper examines a canonical homomorphism from 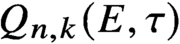$Q_{n,k}(E,\tau )$ to the twisted homogeneous coordinate ring 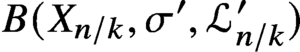$B(X_{n/k},\sigma ',\mathcal {L}^{\prime }_{n/k})$ on the characteristic variety 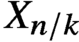$X_{n/k}$ for 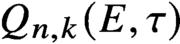$Q_{n,k}(E,\tau )$. When 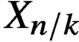$X_{n/k}$ is isomorphic to 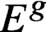$E^g$ or the symmetric power 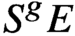$S^gE$, we show that the homomorphism 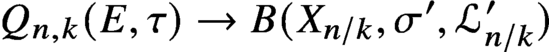$Q_{n,k}(E,\tau ) \to B(X_{n/k},\sigma ',\mathcal {L}^{\prime }_{n/k})$ is surjective, the relations for 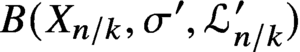$B(X_{n/k},\sigma ',\mathcal {L}^{\prime }_{n/k})$ are generated in degrees 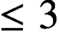$\le 3$ and the noncommutative scheme 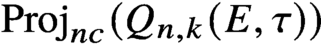$\mathrm {Proj}_{nc}(Q_{n,k}(E,\tau ))$ has a closed subvariety that is isomorphic to 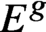$E^g$ or 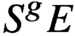$S^gE$, respectively. When 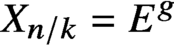$X_{n/k}=E^g$ and 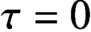$\tau =0$, the results about 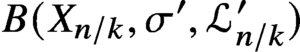$B(X_{n/k},\sigma ',\mathcal {L}^{\prime }_{n/k})$ show that the morphism 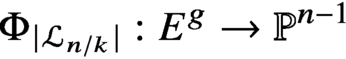$\Phi _{|\mathcal {L}_{n/k}|}:E^g \to \mathbb {P}^{n-1}$ embeds 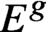$E^g$ as a projectively normal subvariety that is a scheme-theoretic intersection of quadric and cubic hypersurfaces.

Keywords

Elliptic algebraSklyanin algebratwisted homogeneous coordinate ringcharacteristic variety

MSC classification

Primary: 14A22: Noncommutative algebraic geometry
Secondary: 16S38: Rings arising from non-commutative algebraic geometry 16W50: Graded rings and modules 14H52: Elliptic curves
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e4
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Artin, M. and Schelter, W. F., ‘Graded algebras of global dimension $3$’, Adv. Math. 66(2) (1987), 171–216. MR 917738 (88k:16003)CrossRefGoogle Scholar
Atiyah, M. F., ‘Vector bundles over an elliptic curve’, Proc. Lond. Math. Soc. (3) 7 (1957), 414–452. MR 0131423CrossRefGoogle Scholar
Artin, M., Tate, J. and Van den Bergh, M., ‘Some algebras associated to automorphisms of elliptic curves’, in The Grothendieck Festschrift , Vol. I, Progr. Math., 86 (Birkhäuser Boston, Boston, MA, 1990), 33–85. MR 1086882 (92e:14002)Google Scholar
Artin, M., Tate, J. and Van den Bergh, M., ‘Modules over regular algebras of dimension $3$’, Invent. Math. 106(2) (1991), 335–388. MR 1128218 (93e:16055)CrossRefGoogle Scholar
Artin, M. and Van den Bergh, M., ‘Twisted homogeneous coordinate rings’, J. Algebra 133(2) (1990), 249–271. MR 1067406 (91k:14003)CrossRefGoogle Scholar
Artin, M. and Zhang, J. J., ‘Noncommutative projective schemes’, Adv. Math. 109(2) (1994), 228–287. MR 1304753 (96a:14004)CrossRefGoogle Scholar
Belavin, A. A., ‘Discrete groups and integrability of quantum systems’, Funktsional. Anal. i Prilozhen. 14(4) (1980), 18–26, 95. MR 595725Google Scholar
Butler, D. C., ‘Normal generation of vector bundles over a curve’, J. Differential Geom. 39(1) (1994), 1–34. MR 1258911CrossRefGoogle Scholar
Chudnovsky, D. V. and Chudnovsky, G. V., ‘Completely $X$-symmetric $S$-matrices corresponding to theta functions’, Phys. Lett. A 81(2-3) (1981), 105–110. MR 597095CrossRefGoogle Scholar
Catanese, F. and Ciliberto, C., ‘Symmetric products of elliptic curves and surfaces of general type with ${p}_g=q=1$’, J. Algebraic Geom. 2(3) (1993), 389–411. MR 1211993Google Scholar
Cherednik, I. V., ‘On the properties of factorized $S$ matrices in elliptic functions’, Yadernaya Fiz. 36(2) (1982), 549–557. MR 700961Google Scholar
Cherednik, I. V., ‘On $R$-matrix quantization of formal loop groups’, in Group Theoretical Methods in Physics , Vol. II (Yurmala, 1985) (VNU Scientific Press, Utrecht, 1986), 161–180. MR 919789Google Scholar
Chirvasitu, A., Kanda, R. and Smith, S. P., ‘Feigin and Odesskii’s elliptic algebras’, Preprint, 2018, arXiv:1812.09550v3.Google Scholar
Chirvasitu, A., Kanda, R. and Smith, S. P., ‘Finite quotients of powers of an elliptic curve’, Preprint, 2019, arXiv:1905.06710v3.Google Scholar
Chirvasitu, A., Kanda, R. and Smith, S. P., ‘The characteristic variety for Feigin and Odesskii’s elliptic algebras’, Preprint, 2019, arXiv:1903.11798v4.Google Scholar
Chirvasitu, A., Kanda, R. and Smith, S. P., ‘Elliptic R-matrices and Feigin and Odesskii’s elliptic algebras’, Preprint, 2020, arXiv:2006.12283v1.Google Scholar
Chirvasitu, A., Smith, S. P. and Wong, L. Z., ‘Noncommutative geometry of homogenized quantum $\mathrm{sl}\left(2,\mathbb{C}\right)$’, Pacific J. Math. 292(2) (2018), 305–354. MR 3733976CrossRefGoogle Scholar
Feigin, B. L. and Odesskii, A. V., ‘Sklyanin algebras associated with an elliptic curve’, Preprint deposited with Institute of Theoretical Physics of the Academy of Sciences of the Ukrainian SSR, 1989.Google Scholar
Gushel, N. P.${}^{\prime }$, ‘Very ample divisors on projective bundles over an elliptic curve’, Mat. Zametki 47(6) (1990), 15–22, 158. MR 1074523Google Scholar
Hartshorne, R., Algebraic Geometry, Grad. Texts in Math., 52 (Springer-Verlag, New York, 1977). MR 0463157 (57 #3116)Google Scholar
Hulek, K., ‘Projective geometry of elliptic curves’, Astérisque 137 (1986), 143. MR 845383Google Scholar
Keeler, D. S., ‘Criteria for $\sigma$-ampleness’, J. Amer. Math. Soc. 13(3) (2000), 517–532. MR 1758752CrossRefGoogle Scholar
Kempf, G. R., Complex Abelian Varieties and Theta Functions, Universitext (Springer-Verlag, Berlin, 1991). MR 1109495CrossRefGoogle Scholar
Koizumi, S., ‘Theta relations and projective normality of Abelian varieties’, Amer. J. Math. 98(4) (1976), 865–889. MR 480543CrossRefGoogle Scholar
Levasseur, T., ‘Some properties of noncommutative regular graded rings’, Glasg. Math. J. 34(3) (1992), 277–300. MR 1181768 (93k:16045)CrossRefGoogle Scholar
Levasseur, T. and Smith, S. P., ‘Modules over the $4$-dimensional Sklyanin algebra’, Bull. Soc. Math. France 121(1) (1993), 35–90. MR 1207244 (94f:16054)CrossRefGoogle Scholar
Maruyama, M., ‘The theorem of Grauert-Mülich-Spindler’, Math. Ann. 255(3) (1981), 317–333. MR 615853CrossRefGoogle Scholar
Mumford, D., Fogarty, J. and Kirwan, F., Geometric Invariant Theory, 3rd ed., Ergeb. Math. Grenzgeb. (2), 34 (Springer-Verlag, Berlin, 1994). MR 1304906Google Scholar
Mumford, D., ‘Varieties defined by quadratic equations’, in Questions on Algebraic Varieties (C.I.M.E., III Ciclo, Varenna, 1969) (Edizioni Cremonese, Rome, 1970), 29–100. MR 0282975Google Scholar
Mumford, D., Abelian Varieties, Tata Institute of Fundamental Research Studies in Mathematics, 5 (Hindustan Book Agency, New Delhi, 2008; published for the Tata Institute of Fundamental Research, Bombay, corrected reprint of the 2nd [1974] ed.). With appendices by C. P. Ramanujam and Yuri Manin. MR 2514037 (2010e:14040)Google Scholar
Murre, J. P., ‘On contravariant functors from the category of pre-schemes over a field into the category of abelian groups (with an application to the Picard functor)’, Publ. Math. Inst. Hautes Études Sci. 23 (1964), 5–43. MR 0206011CrossRefGoogle Scholar
Odesskii, A. V., ‘Elliptic algebras’, Uspekhi Mat. Nauk 57(6[348]) (2002), 87–122. MR 1991863Google Scholar
Odesskii, A. V. and Feigin, B. L., ‘Sklyanin elliptic algebras’, Funktsional. Anal. i Prilozhen. 23(3) (1989), 45–54, 96. MR 1026987 (91e:16037)Google Scholar
Polishchuk, A., Abelian Varieties, Theta Functions and the Fourier Transform, Cambridge Tracts in Math., 153 (Cambridge University Press, Cambridge, UK, 2003). MR 1987784Google Scholar
Polizzi, F., ‘On surfaces of general type with ${p}_g=q=1,{K}^2=3$’, Collect. Math. 56(2) (2005), 181–234. MR 2154303Google Scholar
Pareschi, G. and Popa, M., ‘Regularity on abelian varieties. II. Basic results on linear series and defining equations’, J. Algebraic Geom. 13(1) (2004), 167–193. MR 2008719CrossRefGoogle Scholar
Sklyanin, E. K., ‘Some algebraic structures connected with the Yang-Baxter equation’, Funktsional. Anal. i Prilozhen. 16(4) (1982), 27–34, 96. MR 684124 (84c:82004)Google Scholar
Sklyanin, E. K., ‘Some algebraic structures connected with the Yang-Baxter equation. Representations of a quantum algebra’, Funktsional. Anal. i Prilozhen. 17(4) (1983), 34–48. MR 725414 (85k:82011)Google Scholar
Smith, S. P., ‘Maps between non-commutative spaces’, Trans. Amer. Math. Soc. 356(7) (2004), 2927–2944. MR 2052602CrossRefGoogle Scholar
Smith, S. P., ‘Corrigendum to “Maps between non-commutative spaces” [Trans. Amer. Math. Soc., 356(7) (2004) 2927-2944]’, Trans. Amer. Math. Soc. 368(7) (2016), 8295–8302 (electronic). MR 2052602 (2005f:14004)CrossRefGoogle Scholar
Sam, S. V. and Snowden, A., ‘Stability patterns in representation theory’, Forum Math. Sigma 3 (2015), e11, 108. MR 3376738CrossRefGoogle Scholar
Smith, S. P. and Stafford, J. T., ‘Regularity of the four-dimensional Sklyanin algebra’, Compos. Math. 83(3) (1992), 259–289. MR 1175941 (93h:16037)Google Scholar
Seidel, P. and Thomas, R., ‘Braid group actions on derived categories of coherent sheaves’, Duke Math. J. 108(1) (2001), 37–108. MR 1831820Google Scholar
Smith, S. P. and Tate, J. T., ‘The center of the $3$-dimensional and $4$-dimensional Sklyanin algebras’, in Proceedings of Conference on Algebraic Geometry and Ring Theory in honor of Michael Artin, Part I (Antwerp, 1992), K-theory 8(1) (1994), 19–63. MR 1273835Google Scholar
Smith, S. P. and Van den Bergh, M., ‘Noncommutative quadric surfaces’, J. Noncommut. Geom. 7(3) (2013), 817–856. MR 3108697CrossRefGoogle Scholar
Sweedler, M. E., Hopf Algebras, Mathematics Lecture Note Series (W. A. Benjamin, Inc., New York, 1969). MR 0252485 (40 #5705)Google Scholar
The Stacks Project Authors, ‘Stacks Project’, 2018, https://stacks.math.columbia.edu.Google Scholar
Tracy, C. A., ‘Embedded elliptic curves and the Yang-Baxter equations’, Phys. D 16(2) (1985), 203–220. MR 796270CrossRefGoogle Scholar
Tu, L. W., ‘Semistable bundles over an elliptic curve’, Adv. Math. 98(1) (1993), 1–26. MR 1212625CrossRefGoogle Scholar
Tate, J. T. and Van den Bergh, M., ‘Homological properties of Sklyanin algebras’, Invent. Math. 124(1-3) (1996), 619–647. MR 1369430 (98c:16057)CrossRefGoogle Scholar
Van den Bergh, M., ‘Blowing up of non-commutative smooth surfaces’, Mem. Amer. Math. Soc. 154(734) (2001). MR 1846352 (2002k:16057)Google Scholar