Article contents
A conjecture strengthening the Zariski dense orbit problem for birational maps of dynamical degree one
Published online by Cambridge University Press: 07 July 2022
Abstract
We formulate a strengthening of the Zariski dense orbit conjecture for birational maps of dynamical degree one. So, given a quasiprojective variety X defined over an algebraically closed field K of characteristic
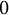 $0$
, endowed with a birational self-map
$0$
, endowed with a birational self-map
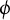 $\phi $
of dynamical degree
$\phi $
of dynamical degree
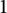 $1$
, we expect that either there exists a nonconstant rational function
$1$
, we expect that either there exists a nonconstant rational function
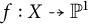 $f:X\dashrightarrow \mathbb {P} ^1$
such that
$f:X\dashrightarrow \mathbb {P} ^1$
such that
 $f\circ \phi =f$
, or there exists a proper subvariety
$f\circ \phi =f$
, or there exists a proper subvariety
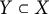 $Y\subset X$
with the property that, for any invariant proper subvariety
$Y\subset X$
with the property that, for any invariant proper subvariety
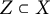 $Z\subset X$
, we have that
$Z\subset X$
, we have that
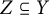 $Z\subseteq Y$
. We prove our conjecture for automorphisms
$Z\subseteq Y$
. We prove our conjecture for automorphisms
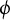 $\phi $
of dynamical degree
$\phi $
of dynamical degree
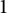 $1$
of semiabelian varieties X. Moreover, we prove a related result for regular dominant self-maps
$1$
of semiabelian varieties X. Moreover, we prove a related result for regular dominant self-maps
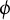 $\phi $
of semiabelian varieties X: assuming that
$\phi $
of semiabelian varieties X: assuming that
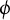 $\phi $
does not preserve a nonconstant rational function, we have that the dynamical degree of
$\phi $
does not preserve a nonconstant rational function, we have that the dynamical degree of
 $\phi $
is larger than
$\phi $
is larger than
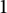 $1$
if and only if the union of all
$1$
if and only if the union of all
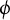 $\phi $
-invariant proper subvarieties of X is Zariski dense. We give applications of our results to representation-theoretic questions about twisted homogeneous coordinate rings associated with abelian varieties.
$\phi $
-invariant proper subvarieties of X is Zariski dense. We give applications of our results to representation-theoretic questions about twisted homogeneous coordinate rings associated with abelian varieties.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
The authors were partially supported by Discovery Grants from the National Science and Engineering Research Council of Canada.
References
- 1
- Cited by



