It is usually believed that wall slip contributes small effects to macroscopic flow characteristics. Here we demonstrate that this is not the case for the thermocapillary migration of a long bubble in a slippery tube. We show that a fraction of the wall slip, with the slip length 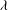 $\lambda $ much smaller than the tube radius
$\lambda $ much smaller than the tube radius 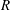 $R$, can make the bubble migrate much faster than without wall slip. This speedup effect occurs in the strong-slip regime where the film thickness
$R$, can make the bubble migrate much faster than without wall slip. This speedup effect occurs in the strong-slip regime where the film thickness 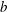 $b$ is smaller than
$b$ is smaller than 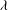 $\lambda $ when the Marangoni number
$\lambda $ when the Marangoni number 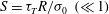 $S= \tau _{T} R/\sigma _{0}~ (\ll 1)$ is below the critical value
$S= \tau _{T} R/\sigma _{0}~ (\ll 1)$ is below the critical value 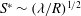 $S^* \sim (\lambda /R)^{1/2}$, where
$S^* \sim (\lambda /R)^{1/2}$, where 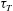 $\tau _{T}$ is the driving thermal stress and
$\tau _{T}$ is the driving thermal stress and 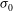 $\sigma _{0}$ is the surface tension. The resulting bubble migration speed is found to be
$\sigma _{0}$ is the surface tension. The resulting bubble migration speed is found to be 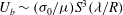 $U_{b} \sim (\sigma _{0}/\mu )S^{3}(\lambda /R)$, which can be more than a hundred times faster than the no-slip result
$U_{b} \sim (\sigma _{0}/\mu )S^{3}(\lambda /R)$, which can be more than a hundred times faster than the no-slip result 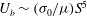 $U_{b} \sim (\sigma _{0}/\mu )S^{5}$ (Wilson, J. Eng. Math., vol. 29, 1995, pp. 205–217; Mazouchi & Homsy, Phys. Fluids, vol. 12, 2000, pp. 542–549), with
$U_{b} \sim (\sigma _{0}/\mu )S^{5}$ (Wilson, J. Eng. Math., vol. 29, 1995, pp. 205–217; Mazouchi & Homsy, Phys. Fluids, vol. 12, 2000, pp. 542–549), with 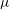 $\mu $ being the fluid viscosity. The change from the fifth power law to the cubic one also indicates a transition from the no-slip state to the strong-slip state, albeit the film thickness always scales as
$\mu $ being the fluid viscosity. The change from the fifth power law to the cubic one also indicates a transition from the no-slip state to the strong-slip state, albeit the film thickness always scales as 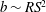 $b\sim RS^{2}$. The formal lubrication analysis and numerical results confirm the above findings. Our results in different slip regimes are shown to be equivalent to those for the Bretherton problem (Liao, Li & Wei, Phys. Rev. Lett., vol. 111, 2013, 136001). Extension to polygonal tubes and connection to experiments are also made. It is found that the slight discrepancy between experiment (Lajeunesse & Homsy, Phys. Fluids, vol. 15, 2003, pp. 308–314) and theory (Mazouchi & Homsy, Phys. Fluids, vol. 13, 2001, pp. 1594–1600) can be interpreted by including wall slip effects.
$b\sim RS^{2}$. The formal lubrication analysis and numerical results confirm the above findings. Our results in different slip regimes are shown to be equivalent to those for the Bretherton problem (Liao, Li & Wei, Phys. Rev. Lett., vol. 111, 2013, 136001). Extension to polygonal tubes and connection to experiments are also made. It is found that the slight discrepancy between experiment (Lajeunesse & Homsy, Phys. Fluids, vol. 15, 2003, pp. 308–314) and theory (Mazouchi & Homsy, Phys. Fluids, vol. 13, 2001, pp. 1594–1600) can be interpreted by including wall slip effects.