Article contents
New scaling laws for turbulent Poiseuille flow with wall transpiration
Published online by Cambridge University Press: 28 March 2014
Abstract
A fully developed, turbulent Poiseuille flow with wall transpiration, i.e. uniform blowing and suction on the lower and upper walls correspondingly, is investigated by both direct numerical simulation (DNS) of the three-dimensional, incompressible Navier–Stokes equations and Lie symmetry analysis. The latter is used to find symmetry transformations and in turn to derive invariant solutions of the set of two- and multi-point correlation equations. We show that the transpiration velocity is a symmetry breaking which implies a logarithmic scaling law in the core of the channel. DNS validates this result of Lie symmetry analysis and hence aids establishing a new logarithmic law of deficit type. The region of validity of the new logarithmic law is very different from the usual near-wall log law and the slope constant in the core region differs from the von Kármán constant and is equal to 0.3. Further, extended forms of the linear viscous sublayer law and the near-wall log law are also derived, which, as a particular case, include these laws for the classical non-transpiring case. The viscous sublayer at the suction side has an asymptotic suction profile. The thickness of the sublayer increase at high Reynolds and transpiration numbers. For the near-wall log law we see an indication that it appears at the moderate transpiration rates (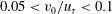 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}0.05<v_0/u_{\tau }<0.1$) and only at the blowing wall. Finally, from the DNS data we establish a relation between the friction velocity
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}0.05<v_0/u_{\tau }<0.1$) and only at the blowing wall. Finally, from the DNS data we establish a relation between the friction velocity 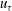 $u_{\tau }$ and the transpiration
$u_{\tau }$ and the transpiration 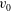 $v_0$ which turns out to be linear at moderate transpiration rates.
$v_0$ which turns out to be linear at moderate transpiration rates.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
Footnotes
The original version of this article was published with the incorrect affiliation for S. Hoyas. A notice detailing this has been published online and in print, and the error rectified in the online PDF and HTML copies.
References
The following corrections have been issued for this article:
- 44
- Cited by
Linked content
Please note have been issued for this article.


