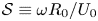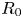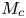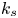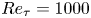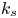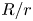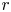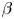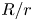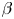JFM Perspectives
The turbulent dynamo
-
- Published online by Cambridge University Press:
- 15 February 2021, P1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
Water entry of spheres into a rotating liquid
-
- Published online by Cambridge University Press:
- 04 February 2021, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Focus on Fluids
The impulsive swirl of a gas
-
- Published online by Cambridge University Press:
- 05 February 2021, F1
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
On the stratification and induced flow in an emptying–filling box driven by a plane vertically distributed source of buoyancy
-
- Published online by Cambridge University Press:
- 04 February 2021, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of hygroscopic aqueous solution droplets undergoing evaporation or vapour absorption
-
- Published online by Cambridge University Press:
- 04 February 2021, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unsteady effects in a hypersonic compression ramp flow with laminar separation
-
- Published online by Cambridge University Press:
- 04 February 2021, A3
-
- Article
- Export citation
Effect of surfactant on the settling of a drop towards a wall
-
- Published online by Cambridge University Press:
- 05 February 2021, A4
-
- Article
- Export citation
Collision rate of bidisperse, hydrodynamically interacting spheres settling in a turbulent flow
-
- Published online by Cambridge University Press:
- 04 February 2021, A5
-
- Article
- Export citation
Manipulation of three-dimensional asymmetries of a turbulent wake for drag reduction
-
- Published online by Cambridge University Press:
- 04 February 2021, A6
-
- Article
- Export citation
Characterization of the shear layer in separated shock/turbulent boundary layer interactions
-
- Published online by Cambridge University Press:
- 05 February 2021, A7
-
- Article
- Export citation
Data-driven prediction of the equivalent sand-grain height in rough-wall turbulent flows
-
- Published online by Cambridge University Press:
- 05 February 2021, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classical and quantum vortex leapfrogging in two-dimensional channels
-
- Published online by Cambridge University Press:
- 05 February 2021, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motion onset in simple yield stress fluids
-
- Published online by Cambridge University Press:
- 05 February 2021, A10
-
- Article
- Export citation
Modelling of particle capture by expanding droplets
-
- Published online by Cambridge University Press:
- 05 February 2021, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transitions of shock interactions on V-shaped blunt leading edges
-
- Published online by Cambridge University Press:
- 05 February 2021, A12
-
- Article
- Export citation
Global and local statistics in turbulent emulsions
-
- Published online by Cambridge University Press:
- 05 February 2021, A13
-
- Article
- Export citation
Diffusion transients in convection rolls
-
- Published online by Cambridge University Press:
- 05 February 2021, A14
-
- Article
- Export citation
Immersed granular collapse: from viscous to free-fall unsteady granular flows
-
- Published online by Cambridge University Press:
- 09 February 2021, A15
-
- Article
- Export citation
Kinematics and dynamics of freely rising spheroids at high Reynolds numbers
-
- Published online by Cambridge University Press:
- 09 February 2021, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Capillary-scale solid rebounds: experiments, modelling and simulations
-
- Published online by Cambridge University Press:
- 09 February 2021, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation