Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-27T20:14:58.056Z Has data issue: false hasContentIssue false
  • English
  • Français

Collision rate of bidisperse, hydrodynamically interacting spheres settling in a turbulent flow

Published online by Cambridge University Press:  04 February 2021

Johnson Dhanasekaran Open the ORCID record for Johnson Dhanasekaran [Opens in a new window] ,
Anubhab Roy Open the ORCID record for Anubhab Roy [Opens in a new window]  and
Donald L. Koch Open the ORCID record for Donald L. Koch [Opens in a new window]
Johnson Dhanasekaran
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY14853, USA
Anubhab Roy
Affiliation:
Department of Applied Mechanics, Indian Institute of Technology Madras, Chennai, Tamil Nadu600036, India
Donald L. Koch*
Affiliation:
Smith School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY14853, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

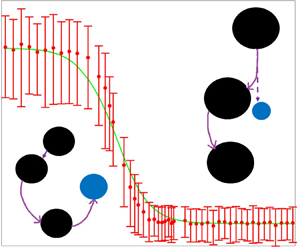
The collisions in a dilute polydisperse suspension of sub-Kolmogorov spheres with negligible inertia settling in a turbulent flow and interacting through hydrodynamics including continuum breakdown on close approach are studied. A statistically significant decrease in ideal collision rate without gravity is resolved via a Lagrangian stochastic velocity-gradient model at Taylor microscale Reynolds number larger than those accessible by current direct numerical simulation capabilities. This arises from the difference between the mean inward velocity and the root-mean-square particle relative velocity. Differential sedimentation, comparable to the turbulent shear relative velocity, but minimally influencing the sampling of the velocity gradient, diminishes the Reynolds number dependence and enhances the ideal collision rate i.e. the rate without interactions. The collision rate is retarded by hydrodynamic interactions between sphere pairs and is governed by non-continuum lubrication as well as full continuum hydrodynamic interactions at larger separations. The collision efficiency (ratio of actual to ideal collision rate) depends on the relative strength of differential sedimentation and turbulent shear, the size ratio of the interacting spheres and the Knudsen number (defined as the ratio of the mean-free path of the gas to the mean radius of the interacting spheres). We develop an analytical approximation to concisely report computed results across the parameter space. This accurate closed form expression could be a critical component in computing the evolution of the size distribution in applications such as water droplets in clouds or commercially valuable products in industrial aggregators.

JFM classification

Drops and Bubbles: Breakup/coalescence Low-Reynolds-number flows: Stokesian dynamics Turbulent Flows: Isotropic turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 912 , 10 April 2021 , A5
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ashurst, W.T., Kerstein, A., Kerr, R. & Gibson, C. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30 (8), 2343–2353.CrossRefGoogle Scholar
Ayala, Q., Grabowski, W. & Wang, L.-P. 2007 A hybrid approach for simulating turbulent collisions of hydrodynamically-interacting particles. J. Comput. Phys. 225 (1), 51–73.CrossRefGoogle Scholar
Ayala, O., Rosa, B., Wang, L.-P. & Grabowski, W. 2008 Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 1. Results from direct numerical simulation. New J. Phys. 10 (7), 075015.CrossRefGoogle Scholar
Balthasar, M., Mauss, F., Knobel, A. & Kraft, M. 2002 Detailed modeling of soot formation in a partially stirred plug flow reactor. Combust. Flame 128 (4), 395–409.CrossRefGoogle Scholar
Batchelor, G. 1982 Sedimentation in a dilute polydisperse system of interacting spheres. Part 1. General theory. J. Fluid Mech. 119, 379–408.CrossRefGoogle Scholar
Batchelor, G. & Green, J. 1972 a The determination of the bulk stress in a suspension of spherical particles to order c 2. J. Fluid Mech. 56 (3), 401–427.CrossRefGoogle Scholar
Batchelor, G. & Green, J.-T. 1972 b The hydrodynamic interaction of two small freely-moving spheres in a linear flow field. J. Fluid Mech. 56 (2), 375–400.CrossRefGoogle Scholar
Beard, K.V. & Ochs III, H.T. 1993 Warm-rain initiation: an overview of microphysical mechanisms. J. Appl. Meteorol. 32 (4), 608–625.2.0.CO;2>CrossRefGoogle Scholar
Blyth, A.M., Lasher-Trapp, S.G., Cooper, W.A., Knight, C.A. & Latham, J. 2003 The role of giant and ultragiant nuclei in the formation of early radar echoes in warm cumulus clouds. J. Atmos. Sci. 60 (21), 2557–2572.2.0.CO;2>CrossRefGoogle Scholar
Brunk, B., Koch, D. & Lion, L. 1998 Turbulent coagulation of colloidal particles. J. Fluid Mech. 364, 81–113.CrossRefGoogle Scholar
Buesser, B. & Pratsinis, S. 2012 Design of nanomaterial synthesis by aerosol processes. Annu. Rev. Chem. Biomol. Engng 3, 103–127.CrossRefGoogle ScholarPubMed
Byeon, S.-H., Lee, B.-K. & Mohan, B.R. 2012 Removal of ammonia and particulate matter using a modified turbulent wet scrubbing system. Sep. Purif. Technol. 98, 221–229.CrossRefGoogle Scholar
Chun, J. & Koch, D. 2005 Coagulation of monodisperse aerosol particles by isotropic turbulence. Phys. Fluids 17 (2), 027102.CrossRefGoogle Scholar
Chun, J., Koch, D.L., Rani, S.L., Ahluwalia, A. & Collins, L.R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.CrossRefGoogle Scholar
Davis, R. 1984 The rate of coagulation of a dilute polydisperse system of sedimenting spheres. J. Fluid Mech. 145, 179–199.CrossRefGoogle Scholar
Dhariwal, R. & Bragg, A. 2018 Small-scale dynamics of settling, bidisperse particles in turbulence. J. Fluid Mech. 839, 594–620.CrossRefGoogle Scholar
Duru, P., Koch, D. & Cohen, C. 2007 Experimental study of turbulence-induced coalescence in aerosols. Intl J. Multiphase Flow 33 (9), 987–1005.CrossRefGoogle Scholar
Feingold, G., Cotton, W.R., Kreidenweis, S.M. & Davis, J.T. 1999 The impact of giant cloud condensation nuclei on drizzle formation in stratocumulus: implications for cloud radiative properties. J. Atmos. Sci. 56 (24), 4100–4117.2.0.CO;2>CrossRefGoogle Scholar
Girimaji, S. & Pope, S. 1990 A diffusion model for velocity gradients in turbulence. Phys. Fluids A: Fluid Dyn. 2 (2), 242–256.CrossRefGoogle Scholar
Grabowski, W.W. & Wang, L.-P. 2013 Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech. 45, 293–324.CrossRefGoogle Scholar
Ireland, P., Bragg, A. & Collins, L. 2016 a The effect of reynolds number on inertial particle dynamics in isotropic turbulence. Part 1. Simulations without gravitational effects. J. Fluid Mech. 796, 617–658.CrossRefGoogle Scholar
Ireland, P., Bragg, A. & Collins, L. 2016 b The effect of reynolds number on inertial particle dynamics in isotropic turbulence. Part 2. Simulations with gravitational effects. J. Fluid Mech. 796, 659–711.CrossRefGoogle Scholar
Jeffrey, D. 1992 The calculation of the low Reynolds number resistance functions for two unequal spheres. Phys. Fluids A: Fluid Dyn. 4 (1), 16–29.CrossRefGoogle Scholar
Jeffrey, D. & Onishi, Y. 1984 Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 139, 261–290.CrossRefGoogle Scholar
Koch, D.L. & Pope, S.B. 2002 Coagulation-induced particle-concentration fluctuations in homogeneous, isotropic turbulence. Phys. Fluids 14 (7), 2447–2455.CrossRefGoogle Scholar
Kolmogorov, A.N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13 (1), 82–85.CrossRefGoogle Scholar
Langmuir, I. 1948 The production of rain by a chain reaction in cumulus clouds at temperatures above freezing. J. Meteorol. 5 (5), 175–192.2.0.CO;2>CrossRefGoogle Scholar
Li, X.-Y., Brandenburg, A., Svensson, G., Haugen, N.E., Mehlig, B. & Rogachevskii, I. 2018 Effect of turbulence on collisional growth of cloud droplets. J. Atmos. Sci. 75 (10), 3469–3487.CrossRefGoogle Scholar
Niu, H., Cheng, W., Pian, W. & Hu, W. 2016 The physiochemical properties of submicron particles from emissions of industrial furnace. World J. Engng 13 (3), 218–224.CrossRefGoogle Scholar
Peng, Y., Lohmann, U., Leaitch, R., Banic, C. & Couture, M. 2002 The cloud albedo-cloud droplet effective radius relationship for clean and polluted clouds from race and fire. ACE. J. Geophys. Res. Atmos. 107 (D11), AAC 1-1–AAC 1-6.CrossRefGoogle Scholar
Pereira, R.M., Moriconi, L. & Chevillard, L. 2018 A multifractal model for the velocity gradient dynamics in turbulent flows. J. Fluid Mech. 839, 430–467.CrossRefGoogle Scholar
Rani, S.L., Dhariwal, R. & Koch, D.L. 2019 Clustering of rapidly settling, low-inertia particle pairs in isotropic turbulence. Part 2. Comparison of theory and dns. J. Fluid Mech. 871, 477–488.CrossRefGoogle Scholar
Reade, W.C. & Collins, L.R. 2000 Effect of preferential concentration on turbulent collision rates. Phys. Fluids 12 (10), 2530–2540.CrossRefGoogle Scholar
Rosa, B., Wang, L.-P., Maxey, M.R. & Grabowski, W.W. 2011 An accurate and efficient method for treating aerodynamic interactions of cloud droplets. J. Comput. Phys. 230 (22), 8109–8133.CrossRefGoogle Scholar
Saffman, P. & Turner, J. 1956 On the collision of drops in turbulent clouds. J. Fluid Mech. 1 (1), 16–30.CrossRefGoogle Scholar
Siebert, H., Wendisch, M., Conrath, T., Teichmann, U. & Heintzenberg, J. 2003 A new tethered balloon-borne payload for fine-scale observations in the cloudy boundary layer. Boundary-Layer Meteorol. 106 (3), 461–482.CrossRefGoogle Scholar
Slingo, A. 1990 Sensitivity of the earth's radiation budget to changes in low clouds. Nature 343 (6253), 49.CrossRefGoogle Scholar
Smoluchowski, M.V. 1918 Versuch einer mathematischen theorie der koagulationskinetik kolloider lösungen. Z. Phys. Chem. 92 (1), 129–168.Google Scholar
Sreenivasan, K. & Kailasnath, P. 1993 An update on the intermittency exponent in turbulence. Phys. Fluids A: Fluid Dyn. 5 (2), 512–514.CrossRefGoogle Scholar
Sundaram, S. & Collins, L. 1997 Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 335, 75–109.CrossRefGoogle Scholar
Sundararajakumar, R. & Koch, D.L. 1996 Non-continuum lubrication flows between particles colliding in a gas. J. Fluid Mech. 313, 283–308.CrossRefGoogle Scholar
Wang, H., Zinchenko, A. & Davis, R. 1994 The collision rate of small drops in linear flow fields. J. Fluid Mech. 265, 161–188.CrossRefGoogle Scholar
Wang, L.-P., Wexler, A.S. & Zhou, Y. 1998 On the collision rate of small particles in isotropic turbulence. I. Zero-inertia case. Phys. Fluids 10 (1), 266–276.CrossRefGoogle Scholar
Yeung, P. & Pope, S. 1989 Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 207, 531–586.CrossRefGoogle Scholar
Zeichner, G. & Schowalter, W. 1977 Use of trajectory analysis to study stability of colloidal dispersions in flow fields. AIChE J. 23 (3), 243–254.CrossRefGoogle Scholar