Article contents
Characterization of the shear layer in separated shock/turbulent boundary layer interactions
Published online by Cambridge University Press: 05 February 2021
Abstract
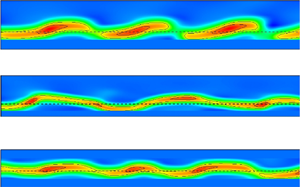
A thorough characterization of the shear layer that exists in large eddy simulation data of three separated, compression ramp-generated shock/turbulent boundary layer interactions is presented. Free stream Mach numbers ahead of the separation shock are 2.9, 7.2 and 9.1. The shear layers produced by the separation in these flows have convective Mach numbers of 1.0, 1.9 and 2.0, respectively. It is found that the separation shear layers share many properties associated with canonical compressible mixing layers. A region of approximate similarity is found in each where it is possible to collapse the mean flow profiles into nearly a single similarity profile. Large mixing-layer-like vortical rollers are found in the shear layers and these are shown to become increasingly three-dimensional with increasing convective Mach number. The relation between the peak turbulence stress and the spreading rate was found to be consistent with mixing layer data and mixing layer theory derived from dimensional analysis. Turbulent kinetic energy and Reynolds stress budget analysis revealed that, although the streamwise turbulence production is greater than the canonical mixing layer, the transfer of turbulence energy by the pressure–strain terms and the energy drain by viscosity terms both show similar behaviour to mixing layer data at matching convective Mach number. As a result, the spreading rate and turbulence anisotropy decrease with increasing  $M_c$. These conclusions are aided by an accurate and direct measurement of the vortex convection velocity determined from enhanced two-point correlations in the shear flow. The usefulness of studying the shock/turbulent boundary layer flow in this manner is emphasized.
$M_c$. These conclusions are aided by an accurate and direct measurement of the vortex convection velocity determined from enhanced two-point correlations in the shear flow. The usefulness of studying the shock/turbulent boundary layer flow in this manner is emphasized.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 18
- Cited by



