Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-08T22:13:40.478Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady turbulent density currents on a slope in a rotating fluid

Published online by Cambridge University Press:  02 April 2014

G. E. Manucharyan ,
W. Moon ,
F. Sévellec ,
A. J. Wells ,
J.-Q. Zhong  and
J. S. Wettlaufer
G. E. Manucharyan*
Affiliation:
Yale University, New Haven, CT 06520, USA
W. Moon
Affiliation:
Yale University, New Haven, CT 06520, USA
F. Sévellec
Affiliation:
Yale University, New Haven, CT 06520, USA University of Southampton, Southampton SO14 3ZH, UK
A. J. Wells
Affiliation:
Yale University, New Haven, CT 06520, USA University of Oxford, Oxford OX1 3PU, UK
J.-Q. Zhong
Affiliation:
Yale University, New Haven, CT 06520, USA Tongji University, Shanghai 200092, PR China
J. S. Wettlaufer
Affiliation:
Yale University, New Haven, CT 06520, USA University of Oxford, Oxford OX1 3PU, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the dynamics of actively entraining turbulent density currents on a conical sloping surface in a rotating fluid. A theoretical plume model is developed to describe both axisymmetric flow and single-stream currents of finite angular extent. An analytical solution is derived for flow dominated by the initial buoyancy flux and with a constant entrainment ratio, which serves as an attractor for solutions with alternative initial conditions where the initial fluxes of mass and momentum are non-negligible. The solutions indicate that the downslope propagation of the current halts at a critical level where there is purely azimuthal flow, and the boundary layer approximation breaks down. Observations from a set of laboratory experiments are consistent with the dynamics predicted by the model, with the flow approaching a critical level. Interpretation in terms of the theory yields an entrainment coefficient 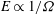$E\propto 1/\Omega $ where the rotation rate is 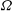$\Omega $. We also derive a corresponding theory for density currents from a line source of buoyancy on a planar slope. Our theoretical models provide a framework for designing and interpreting laboratory studies of turbulent entrainment in rotating dense flows on slopes and understanding their implications in geophysical flows.

JFM classification

Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Rotating flows Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 746 , 10 May 2014 , pp. 405 - 436
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, W. D. & Turner, J. S. 1969 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 37, 51–80.Google Scholar
Borenäs, K. & Wåhlin, A. K. 2000 Limitations of the streamtube model. Deep-Sea Res. I 47, 1333–1350.Google Scholar
Carmack, E. C. 2000 The Arctic Ocean’s freshwater budget: sources, storage and export. In Proceedings of the NATO Advanced Research Workshop on The Freshwater Budget of the Arctic Ocean (ed. Lewis, E. L.), pp. 91–126. Kluwer.Google Scholar
Cenedese, C. & Adduce, C. 2008 Mixing in a density-driven current flowing down a slope in a rotating fluid. J. Fluid Mech. 604, 369–388.Google Scholar
Cenedese, C. & Adduce, C. 2010 A new parameterisation for entrainment in overflows. J. Phys. Oceanogr. 40 (8), 1835–1850.Google Scholar
Cenedese, C., Whitehead, J. A., Ascarelli, T. A. & Ohiwa, M. 2004 A dense current flowing down a sloping bottom in a rotating fluid. J. Phys. Oceanogr. 34 (1), 188–203.Google Scholar
Cleveland, W. S. 1981 LOWESS: a programme for smoothing scatterplots by robust locally weighted regression. Am. Statist. 35 (1), 54.Google Scholar
Ellison, T. H. & Turner, J. S. 1959 Turbulent entrainment in stratified flows. J. Fluid Mech. 6 (3), 423–448.Google Scholar
Garratt, J. R., Howells, P. A. C. & Kowalczyk, E. 1989 The behaviour of dry cold fronts travelling along a coastline. Mon. Weath. Rev. 117 (6), 1208–1220.Google Scholar
Griffiths, R. W. 1986 Gravity currents in rotating systems. Annu. Rev. Fluid Mech. 18, 59–89.Google Scholar
Hughes, G. O. & Griffiths, R. W. 2006 A simple convective model of the global overturning circulation, including effects of entrainment into sinking regions. Ocean Model. 12 (1–2), 46–79.Google Scholar
Hunt, G. R. & Kaye, N. G. 2001 Virtual origin correction for lazy turbulent plumes. J. Fluid Mech. 435, 377–396.Google Scholar
Huppert, H. E. 2006 Gravity currents: a personal perspective. J. Fluid Mech. 554, 299–322.CrossRefGoogle Scholar
Ivanov, V. V., Shapiro, G. I., Huthnance, J. M., Aleynik, D. L. & Golovin, P. N. 2004 Cascades of dense water around the world ocean. Prog. Oceanogr. 60 (1), 47–98.Google Scholar
Lane-Serff, G. F. & Baines, P. G. 1998 Eddy formation by dense flows on slopes in a rotating fluid. J. Fluid Mech. 363, 229–252.Google Scholar
Lignieres, F., Catala, C. & Mangeney, A. 1996 Angular momentum transfer in pre-main-sequence stars of intermediate mass. Astron. Astrophys. 314 (2), 465–476.Google Scholar
Linden, P. F.2000 Convection in the environment. In Perspectives in Fluid Mechanics, chap. 6, pp. 303–321. Cambridge University Press.Google Scholar
McKee, C. F. & Ostriker, E. C. 2007 Theory of star formation. Annu. Rev. Astron. Astrophys. 45, 565–687.Google Scholar
Monaghan, J. J. 2007 Gravity current interaction with interfaces. Annu. Rev. Fluid Mech. 39, 245–261.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234 (1196), 1–32.Google Scholar
Nof, D. 1983 The translation of isolated cold eddies on a sloping bottom. Deep-Sea Res. A 30 (2), 171–182.Google Scholar
Pratt, L. J., Riemenschneider, U. & Helfrich, K. R. 2007 A transverse hydraulic jump in a model of the Faroe Bank Channel outflow. Ocean Model. 19, 1–9.Google Scholar
Price, J. F. & Baringer, M. O. 1994 Outflows and deep-water production by marginal seas. Prog. Oceanogr. 33 (3), 161–200.Google Scholar
Princevac, M., Fernando, H. J. S. & Whiteman, C. D. 2005 Turbulent entrainment into natural gravity-driven flows. J. Fluid Mech. 533, 259–268.Google Scholar
Rieutord, M. & Zahn, J. P. 1995 Turbulent plumes in stellar convective envelopes. Astron. Astrophys. 296 (1), 127–138.Google Scholar
Schlichting, H. 1968 Boundary Layer Theory. 6th edn. McGraw Hill.Google Scholar
Shapiro, G. I. & Hill, A. E. 1997 Dynamics of dense water cascades at the shelf edge. J. Phys. Oceanogr. 27 (11), 2381–2394.2.0.CO;2>CrossRefGoogle Scholar
Shapiro, G. I. & Zatsepin, A. G. 1997 Gravity current down a steeply inclined slope in a rotating fluid. Ann. Geophys. 15, 366–374.Google Scholar
Simpson, J. E. 1997 Gravity Currents in the Environment and the Laboratory. Cambridge University Press.Google Scholar
Smith, P. C. 1975 A streamtube model for bottom boundary currents in the ocean. Deep-Sea Res. Oceanogr. Abstr. 22 (12), 853–873.Google Scholar
Sutherland, B. R., Nault, J., Yewchuk, K. & Swaters, G. E. 2004 Rotating dense currents on a slope. Part 1. Stability. J. Fluid Mech. 508, 241–264.Google Scholar
Taylor, G. I. 1920 Tidal friction in the Irish Sea. Phil. Trans. R. Soc. Lond. A 220, 1–33.Google Scholar
Timmermans, M. -L., Francis, J., Proshutinsky, A. & Hamilton, L. 2009 Taking stock of Arctic sea ice and climate. Bull. Am. Meteorol. Soc. 90 (9), 1351–1353.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar
Wåhlin, A. K. & Cenedese, C. 2006 How entraining density currents influence the stratification in a one-dimensional ocean basin. Deep-Sea Res. II 53 (1–2), 172–193.Google Scholar
Wåhlin, A. K., Darelius, E., Cenedese, C. & Lane-Serff, G. F. 2008 Laboratory observations of enhanced entrainment in dense overflows in the presence of submarine canyons and ridges. Deep-Sea Res. I 55, 737–750.Google Scholar
Wåhlin, A. K. & Walin, G. 2001 Downward migration of dense bottom currents. Environ. Fluid Mech. 1, 257–279.Google Scholar
Wells, M. G. 2007 Influence of Coriolis forces on turbidity currents and sediment deposition. In Particle-Laden Flow: From Geophysical to Kolmogorov Scales (ed. Geurts, B. J., Clercx, H. & Uijttewaal, W.), vol. 11, pp. 331–343. Springer.Google Scholar
Wells, M. G., Cenedese, C. & Caulfield, C. P. 2010 The relationship between flux coefficient and entrainment ratio in density currents. J. Phys. Oceanogr. 40 (12), 2713–2727.Google Scholar
Wells, M. G. & Wettlaufer, J. S. 2005 Two-dimensional density currents in a confined basin. Geophys. Astrophys. Fluid Dyn. 99 (3), 199–218.Google Scholar
Wells, M. G. & Wettlaufer, J. S. 2007 The long-term circulation driven by density currents in a two-layer stratified basin. J. Fluid Mech. 572, 37–58.Google Scholar
Wilchinsky, A. V., Feltham, D. L. & Holland, P. R. 2007 The effect of a new drag-law parameterisation on ice shelf water plume dynamics. J. Phys. Oceanogr. 37 (7), 1778–1792.CrossRefGoogle Scholar
Wirth, A. 2009 On the basic structure of oceanic gravity currents. Ocean Dyn. 59 (4), 551–563.Google Scholar
Wirth, A. 2011 Estimation of friction parameters in gravity currents by data assimilation in a model hierarchy. Ocean Sci. Discus. 8 (1), 159–187.Google Scholar
Wobus, F., Shapiro, G. I., Maqueda, M. A. M. & Huthnance, J. M. 2011 Numerical simulations of dense water cascading on a steep slope. J. Mar. Res. 69, 391–415.Google Scholar
Youdin, A. N. & Shu, F. H. 2002 Planetesimal formation by gravitational instability. Astrophys. J. 580 (1), 494–505.Google Scholar