Cover: Dark-field OM microstructure of experimental alloys after 425°C/24h. [K. Liu, X. Chen: Improvement in elevated-temperature properties of Al-13% Si piston alloys by dispersoid strengthening via Mn addition. p. 3430].
Invited Feature Paper
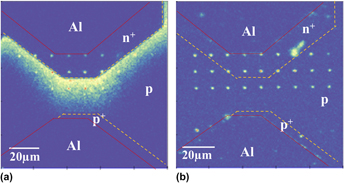
Electrically controllable position-controlled color centers created in SiC pn junction diode by proton beam writing
-
- Published online by Cambridge University Press:
- 04 September 2018, pp. 3355-3361
-
- Article
- Export citation
Invited Paper
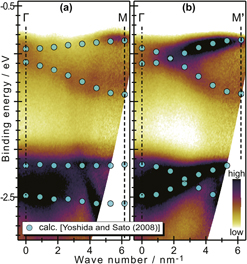
Anisotropic valence band dispersion of single crystal pentacene as measured by angle-resolved ultraviolet photoelectron spectroscopy
-
- Published online by Cambridge University Press:
- 07 September 2018, pp. 3362-3370
-
- Article
- Export citation
Article
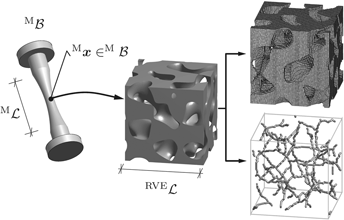
Skeletonization-based beam finite element models for stochastic bicontinuous materials: Application to simulations of nanoporous gold
-
- Published online by Cambridge University Press:
- 27 July 2018, pp. 3371-3382
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
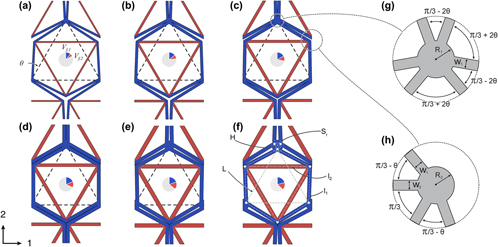
Mechanical characterization of a bonded tailorable coefficient of thermal expansion lattice with near optimal performance
-
- Published online by Cambridge University Press:
- 26 October 2018, pp. 3383-3397
-
- Article
- Export citation
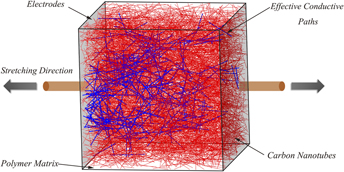
Comprehensive analysis on the electrical behavior of highly stretchable carbon nanotubes/polymer composite through numerical simulation
-
- Published online by Cambridge University Press:
- 04 September 2018, pp. 3398-3407
-
- Article
- Export citation
N-doped ordered mesoporous carbon prepared by solid–solid grinding for supercapacitors
-
- Published online by Cambridge University Press:
- 13 July 2018, pp. 3408-3417
-
- Article
- Export citation
Effects of cell parameters at low strain rates on the mechanical properties of metallic foams of Al and 7075-T6 alloy processed by pressurized infiltration casting method
-
- Published online by Cambridge University Press:
- 04 September 2018, pp. 3418-3429
-
- Article
- Export citation
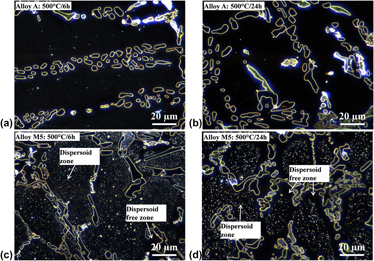
Improvement in elevated-temperature properties of Al–13% Si piston alloys by dispersoid strengthening via Mn addition
-
- Published online by Cambridge University Press:
- 11 May 2018, pp. 3430-3438
-
- Article
- Export citation
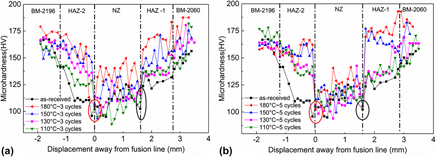
Effect of thermal cycles on the laser beam welded joint of AA2060 alloys
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 3439-3448
-
- Article
- Export citation
Development of ultrafine grained Al 7075 by cryogenic temperature large strain extrusion machining
-
- Published online by Cambridge University Press:
- 20 September 2018, pp. 3449-3457
-
- Article
- Export citation
Effect of cooling rate on growth and transformation of primary Mg2Si in Al–Mg2Si in situ composites
-
- Published online by Cambridge University Press:
- 11 May 2018, pp. 3458-3465
-
- Article
- Export citation
Effect of zinc and rare-earth element addition on mechanical, corrosion, and biological properties of magnesium
-
- Published online by Cambridge University Press:
- 18 September 2018, pp. 3466-3478
-
- Article
- Export citation
Investigation on precipitation phenomena and mechanical properties of Ni–25Cr–20Co alloys aged at high temperature
-
- Published online by Cambridge University Press:
- 25 September 2018, pp. 3479-3489
-
- Article
- Export citation
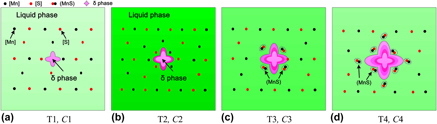
Effect of MnS precipitation on solute equilibrium partition coefficients in high sulfur steel during solidification
-
- Published online by Cambridge University Press:
- 05 June 2018, pp. 3490-3500
-
- Article
- Export citation
Investigation of hydrogen embrittlement in 12Cr2Mo1R(H) steel
-
- Published online by Cambridge University Press:
- 24 September 2018, pp. 3501-3511
-
- Article
- Export citation
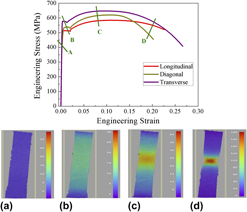
Anisotropy and microstructural evolutions of X70 pipeline steel during tensile deformation
-
- Published online by Cambridge University Press:
- 26 June 2018, pp. 3512-3520
-
- Article
- Export citation
Laser solid forming assisted by friction stir processing for preparation of Ni–16Cr–8Fe alloys: Crack repairing and grain refinement
-
- Published online by Cambridge University Press:
- 27 June 2018, pp. 3521-3529
-
- Article
- Export citation
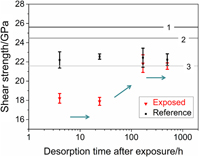
Hydrogen embrittlement of tungsten induced by deuterium plasma: Insights from nanoindentation tests
-
- Published online by Cambridge University Press:
- 04 September 2018, pp. 3530-3536
-
- Article
- Export citation
Corrigendum
Hydrothermal synthesis of gold nanoplates and their structure-dependent LSPR properties – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 05 October 2018, p. 3537
-
- Article
-
- You have access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
JMR volume 33 issue 20 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 October 2018, pp. f1-f5
-
- Article
-
- You have access
- Export citation