Research Article
The Hausdorff Moment Problem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 257-265
-
- Article
-
- You have access
- Export citation
A Global Existence and Uniqueness Theorem for Ordinary Differential Equations of Generalized Order
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 267-271
-
- Article
-
- You have access
- Export citation
Certain nth Order Differential Inequalities in the Complex Plane
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 273-277
-
- Article
-
- You have access
- Export citation
On the Convergence Vector Space ℒ,(E, F) and its Dual Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 279-284
-
- Article
-
- You have access
- Export citation
On a Conjecture of Graham Concerning a Sequence of Integers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 285-287
-
- Article
-
- You have access
- Export citation
On Almost Contingent Manifolds of Second Class with Applications in Relativity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 289-295
-
- Article
-
- You have access
- Export citation
On Square Pseudo-Lucas Numbers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 297-303
-
- Article
-
- You have access
- Export citation
Dimension Theory via Reduced Bisector Chains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 305-311
-
- Article
-
- You have access
- Export citation
Order Characterization of the Complex Field
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 313-318
-
- Article
-
- You have access
- Export citation
Continuous Rings and Rings of Quotients
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 319-324
-
- Article
-
- You have access
- Export citation
Automorphisms of Full II1 Factors, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 325-328
-
- Article
-
- You have access
- Export citation
Content Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 329-334
-
- Article
-
- You have access
- Export citation
A Characterization of Soft Hypergraphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 335-337
-
- Article
-
- You have access
- Export citation
On Weak Vitali Covering Properties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 339-345
-
- Article
-
- You have access
- Export citation
Applications of Variants of the Hölder Inequality and its Inverses: Extensions of Barnes, Marshall-Olkin, and Nehari Inequalities.
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 347-354
-
- Article
-
- You have access
- Export citation
On Earle's mod n Relative Teichmüller Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 355-360
-
- Article
-
- You have access
- Export citation
The Chinese Remainder Theorem and the Invariant Basis Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 361-362
-
- Article
-
- You have access
- Export citation
Paracompactness for Ordered Sums
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 363-364
-
- Article
-
- You have access
- Export citation
Note on Attaching Dold Fibrations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 365-367
-
- Article
-
- You have access
- Export citation
A Note on Derivations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 369-370
-
- Article
-
- You have access
- Export citation

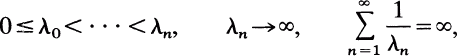
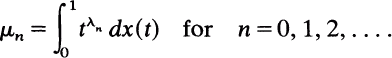
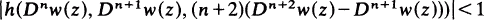
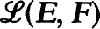 the space of continuous linear mappings from E into F In this paper, we investigate the continuous convergence structure (c-structure) on.
the space of continuous linear mappings from E into F In this paper, we investigate the continuous convergence structure (c-structure) on. 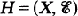 denotes the resulting convergence vector space (cvs).
denotes the resulting convergence vector space (cvs).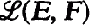 making evaluation a continuous mapping.
making evaluation a continuous mapping.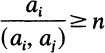
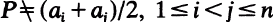 , then
, then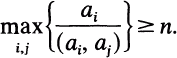



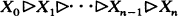 such that dim X
such that dim X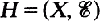 is a subtree of a tree (SOFT) hypergraph if there exists a tree T such that X=V(T) and for each
is a subtree of a tree (SOFT) hypergraph if there exists a tree T such that X=V(T) and for each 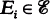 there is a subtree T
there is a subtree T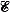 has the Helly property and
has the Helly property and 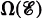 , the intersection graph of
, the intersection graph of 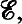 is chordal. Results of Berge and Gavril have previously shown these to be necessary conditions.
is chordal. Results of Berge and Gavril have previously shown these to be necessary conditions.