Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-20T16:23:57.193Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain nth Order Differential Inequalities in the Complex Plane

Published online by Cambridge University Press:  20 November 2018

H. S. Al-Amiri
H. S. Al-Amiri*
Affiliation:
Department of Mathematics, Bowling Green State University, Bowling Green, OHIO 43403
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let w(z) be regular in the unit disc U:|z|<l, with w(0) = 0 and let h(r, s, t) be a complex function defined in a domain D of C3. The author determines conditions on h such that if

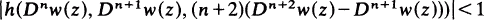
z∈U, then |w(z)|< 1 for z ∈ U and n= 0, 1, 2, …. Here Dnw(z) = (z/(l-z)n+1*w(z), where * stands for the Hadamard product (convolution). Some applications of the results to certain differential equations are given.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 21 , Issue 3 , 01 September 1978 , pp. 273 - 277
Copyright
Copyright © Canadian Mathematical Society 1978

References

1. Jack, I. S., Functions starlike and convex of order a, J. London Math. Soc. (2) 3 (1971), 469-474.Google Scholar
2. Miller, S. S., A class of differential inequalities implying boundedness, III. J. of Math. 20 (1976), 647-649.Google Scholar
3. Miller, S. S. and Mocanu, P. T., Second order differential inequalities in the complex plane, to appear.Google Scholar
4. Ruscheweyh, S., New criteria for univalent functions, Proc. Amer. Math. Soc. vol. 49 (1975), 109-115.Google Scholar