Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-20T16:34:09.168Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of Soft Hypergraphs

Published online by Cambridge University Press:  20 November 2018

Peter J. Slater
Peter J. Slater*
Affiliation:
Applied Mathematics Division 5121, Sandia Laboratories, Albuquerque, New Mexico 87115
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

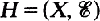A hypergraph is a subtree of a tree (SOFT) hypergraph if there exists a tree T such that X=V(T) and for each 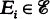there is a subtree T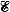i of T such that Ei = V(Ti). It is shown that H is a SOFT hypergraph if and only if has the Helly property and 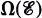, the intersection graph of 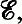is chordal. Results of Berge and Gavril have previously shown these to be necessary conditions.

Keywords

chordal graphHelly propertyhypergraphMenger systemtree.05005
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 21 , Issue 3 , 01 September 1978 , pp. 335 - 337
Copyright
Copyright © Canadian Mathematical Society 1978

References

1. Berge, C., Graphs and Hypergraphs, North-Holland, Amsterdam, 1973.Google Scholar
2. Cockayne, E. J., Hedetniemi, S. T. and Slater, P. J., Matchings and Transversals in Hypergraphs, Domination and Independence in Trees, to appear in JCT(B).Google Scholar
3. Dirac, G. A., On rigid circuit graphs, Abh. Math. Sem. Univ. Hamburg 25, 71-76 (1961).Google Scholar
4. Gavril, F., The Intersection Graphs of Subtrees in Trees Are Exactly the Chordal Graphs, JCT(B) 16, 47-56(1974).Google Scholar
5. Rose, D. J., Triangulated Graphs and the Elimination Process, J. Math. Anal. Appl. 32, 597-609(1970).Google Scholar