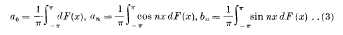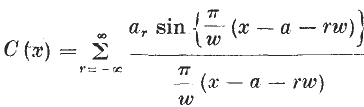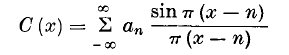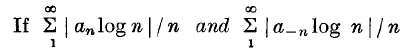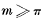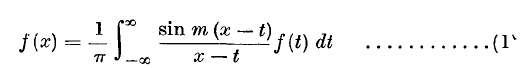Research Article
A Theorem on Bordering Symmetrical Determinants whose Elements are of the form araaas
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 189-192
-
- Article
-
- You have access
- Export citation
Note on Numerical Integration
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 139-148
-
- Article
-
- You have access
- Export citation
Sketch of the History of Mathematics in Scotland to the end of the 18th Century: Part I.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-18
-
- Article
-
- You have access
- Export citation
Sketch of the History of Mathematics in Scotland to the end of the 18th Century: Part II
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 71-93
-
- Article
-
- You have access
- Export citation
Infinitesimal Analysis of an arc in n-space
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 149-159
-
- Article
-
- You have access
- Export citation
An Application of Abel's Lemma to Double Series1
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 193-196
-
- Article
-
- You have access
- Export citation
On general curves lying on a quadric
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 19-30
-
- Article
-
- You have access
- Export citation
The solution of Cauchy's Problem for linear partial differential equations, with constant coefficients, by means of integrals involving complex variables
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 94-103
-
- Article
-
- You have access
- Export citation
Some Properties of a Family of Curves on a Surface
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 160-165
-
- Article
-
- You have access
- Export citation
A Note on Double Limits
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 197-198
-
- Article
-
- You have access
- Export citation
On the uninodal quartic curve
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 31-38
-
- Article
-
- You have access
- Export citation
A special Pencil of Binary Quartics
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 104-110
-
- Article
-
- You have access
- Export citation
A General Formula of Polynomial Interpolation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 199-203
-
- Article
-
- You have access
- Export citation
On Differentiating a Matrix
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 111-128
-
- Article
-
- You have access
- Export citation
On the meaning of an equation in dual coordinates
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 39-40
-
- Article
-
- You have access
- Export citation
Note on the Elementary Divisors of Some Related Determinants
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 166-168
-
- Article
-
- You have access
- Export citation
Remarks on the Algebra of the 4-nodal Cubic Surface
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 204-208
-
- Article
-
- You have access
- Export citation
The “Fourier” Theory of the Cardinal Function
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 169-176
-
- Article
-
- You have access
- Export citation
On the Cardinal Function of Interpolation Theory
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 41-46
-
- Article
-
- You have access
- Export citation
On Hardy's Theory of m-Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 129-134
-
- Article
-
- You have access
- Export citation

 is not infinite within the range considered, and it is therefore hardly a matter for surprise that the degree of accuracy obtainable by the use of these rules in the case of a curve which
is not infinite within the range considered, and it is therefore hardly a matter for surprise that the degree of accuracy obtainable by the use of these rules in the case of a curve which 
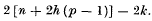
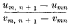 by
by 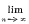
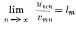 , for all values of
, for all values of 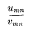 exists, being
exists, being 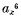 of a pencil of binary quartics is known, the pencil itself is determined in five ways. The explicit determination of the pencil in terms of the irrational invariants of
of a pencil of binary quartics is known, the pencil itself is determined in five ways. The explicit determination of the pencil in terms of the irrational invariants of 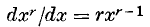 is well known. So also is the theorem that if
is well known. So also is the theorem that if 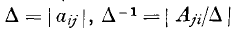 concerning a determinant Λ and its reciprocal expressed by means of cofactors
concerning a determinant Λ and its reciprocal expressed by means of cofactors 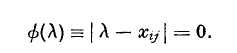
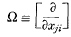 acting upon a function of a matrix
acting upon a function of a matrix 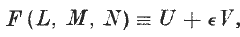


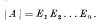
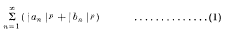
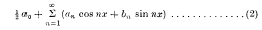
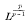 . When
. When