No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 20 January 2009
If L, M, N denote Prof. Study's Dual Coordinates of a straight line (see Proc. Edinburgh Math. Soc., 44 (1926), 90–97), any (homogeneous) equation F (L, M, N) = 0 must define a certain system of lines. By the nature of dual numbers we must have
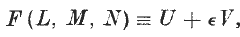
where U and V are functions of l, m, n, λ, μ, ν, the ordinary (Pluckerian) coordinates. Since F = 0 implies U = 0 and V = 0 the system of lines is a congruence. But it is a congruence of a very special kind, whose nature will now be considered.
You have
Access