Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-18T04:56:38.122Z Has data issue: false hasContentIssue false
  • English
  • Français

On Hardy's Theory of m-Functions

Published online by Cambridge University Press:  20 January 2009

E. T. Copson
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

§1. The Cardinal Function of Interpolation Theory is the function

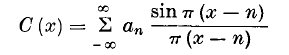
which takes the values an at the points x = n. Ferrar has recently proved

Theorem1. If 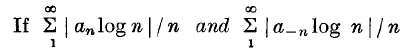are convergent, C(x)is an m-function3for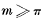

This means that C(x) is a solution of the intergral equation

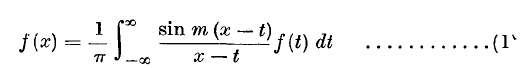
Ferrar's proof deals with functions of a real variable and involves some rather difficult double limit considerations.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 1 , Issue 2 , March 1928 , pp. 129 - 134
Copyright
Copyright © Edinburgh Mathematical Society 1928

References

page 129 note 1 This function was introduced by ProfWhittaker, , Proc. Roy. Soc. Edin., 35 (1915), 181–194.CrossRefGoogle Scholar

page 129 note 2 ibid., 46 (1926), 323–333; in particular 330–333.

page 129 note 3 The theory of m-functions is due to ProfHardy, , Proc. Lond. Math. Soc., (2), 7 (1909), 445–472.CrossRefGoogle Scholar

page 129 note 4 §§3, 4 have been rewritten in accordance with the valuable suggestions of Mr Ferrar, W. L., who kindly read the paper in manuscript.Google Scholar

page 130 note 1 It is an elementary consequence of the result (given in Whittaker and Watson, Modern Analysis (1920), § 22. 737), .Google Scholar

page 130 note 2 See Bromwich, Infinite Series (1926). § 49.Google Scholar

page 133 note 1 Proc. Boy. Soc. Edin., 47 (1927), 230–242.Google ScholarThe particular case p = 1 was previously discussed by Whittaker, J. M., Proc. Edin. Math. Soc., (2) (1927), 41–46.CrossRefGoogle Scholar

page 134 note 1 Compare the rather similar theorems given by Hardy, , loc. cit., 457, 459.Google Scholar