Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-18T04:30:30.147Z Has data issue: false hasContentIssue false
  • English
  • Français

On general curves lying on a quadric

Published online by Cambridge University Press:  20 January 2009

H. F. Baker
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Introduction. The present note, though in continuation of the preceding one dealing with rational curves, is written so as to be independent of this. It is concerned to prove that if a curve of order n, and genus p, with k cusps, or stationary points, lying on a quadric, Ω, in space of any number of dimensions, is such that itself, its tangents, its osculating planes, … , and finally its osculating (h – 1)-folds, all lie on the quadric Ω, then the number of its osculating h-folds which lie on the quadric is

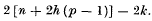
Two proofs of this result are given, in §§ 4 and 5.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 1 , Issue 1 , May 1927 , pp. 19 - 30
Copyright
Copyright © Edinburgh Mathematical Society 1927

References

page 19 note 1 Proc. Edin. Math. Soc, XLIV, 1926, p. 131.Google Scholar

page 25 note 1 For instance, if we can have a rational quintic curve, with its tangents, lying upon a quadric in space of four dimensions (n = 5, h = 2, r = 4), the result of the formula would otherwise be that there are two of its osculating planes upon the quadric. In the preceding paper, dealing with rational curves, we have supposed the curve of order n to lie in space of n dimensions.