No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 20 January 2009
I. If the Jacobian sextic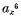 
of a pencil of binary quartics is known, the pencil itself is determined in five ways. The explicit determination of the pencil in terms of the irrational invariants of 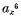has been effected by Stephanos.
There are two known cases in which a pencil of quartics admits of rational determination from its Jacobian. In these, the rationally determinable pencil differentiates itself algebraically from its remaining four co-Jacobian pencils.
page 104 note 1 Mem. I'lnstitut, 27 (1883), 2.Google Scholar
page 104 note 2 The Null Pencil of Binary Quartics, Proc. Lond. Math. Soc., 2, 23 (1923) 317–325.Google Scholar
page 106 note 1 This might be seen most simply by taking the two linearly independent members in the form 
page 108 note 1 Compare Proc. L.M.S. loc. cit.Google Scholar
page 110 note 1 (For the theory of pedo-parallelism of inscribed triangles of a circle, see Proc. Camb. Phil. Soc. 23 (1926), p. 253.Google Scholar
You have
Access