A Note on Double Limits

Extract

Let u_mn, v_mn be functions of m and n, v_mn being real and positive for all positive values of m and n. Suppose that either v_mn increases steadily to infinity with n, or that u_mn both tend to zero (the latter steadily) as n → ∞, for any fixed value of m. Denote 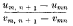by w_mn, and assume that 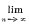w_mn exists for every value of m, being denoted by l^m. Then from Stolz' extension of a result proved by Cauchy, and an allied theorem, we have 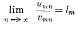, for all values of m. It follows from Pringsheim's Theorem that if the double limit of 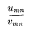exists, being l, then l_m → l as m → ∞.