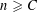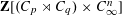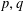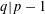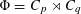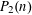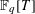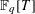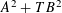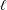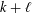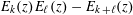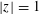Research Article
HILBERT TRANSFORMS ALONG LIPSCHITZ DIRECTION FIELDS: A LACUNARY MODEL
- Part of:
-
- Published online by Cambridge University Press:
- 09 February 2017, pp. 351-363
-
- Article
- Export citation
PRIMES AND PRIME IDEALS IN SHORT INTERVALS
- Part of:
-
- Published online by Cambridge University Press:
- 09 February 2017, pp. 364-371
-
- Article
-
- You have access
- HTML
- Export citation
ILLUMINATION OF CONVEX BODIES WITH MANY SYMMETRIES
- Part of:
-
- Published online by Cambridge University Press:
- 16 February 2017, pp. 372-382
-
- Article
- Export citation
ENVELOPES FOR SETS AND FUNCTIONS: REGULARIZATION AND GENERALIZED CONJUGACY
- Part of:
-
- Published online by Cambridge University Press:
- 23 February 2017, pp. 383-432
-
- Article
- Export citation
WEIGHTED INEQUALITIES FOR MARTINGALE TRANSFORMS AND STOCHASTIC INTEGRALS
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2017, pp. 433-450
-
- Article
- Export citation
STABLY FREE MODULES OVER
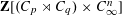 $\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{n}]$ ARE FREE
$\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{n}]$ ARE FREE
- Part of:
-
- Published online by Cambridge University Press:
- 22 February 2017, pp. 451-461
-
- Article
- Export citation
ON THE DETERMINATION OF STAR BODIES FROM THEIR HALF-SECTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 462-468
-
- Article
- Export citation
MINIMIZING DIRICHLET EIGENVALUES ON CUBOIDS OF UNIT MEASURE
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 469-482
-
- Article
- Export citation
ON THE LEAST SQUAREFREE NUMBER IN AN ARITHMETIC PROGRESSION
- Part of:
-
- Published online by Cambridge University Press:
- 23 March 2017, pp. 483-498
-
- Article
- Export citation
AN EXPLICIT DIAGONAL RESOLUTION FOR A NON-ABELIAN METACYCLIC GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 23 March 2017, pp. 499-517
-
- Article
- Export citation
NON-UNIFORM TRICHOTOMIES AND ARBITRARY GROWTH RATES
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2017, pp. 518-537
-
- Article
- Export citation
ISOMETRIC REPRESENTATION OF LIPSCHITZ-FREE SPACES OVER CONVEX DOMAINS IN FINITE-DIMENSIONAL SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 04 April 2017, pp. 538-552
-
- Article
- Export citation
ON SOME MULTIPLE CHARACTER SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2017, pp. 553-560
-
- Article
- Export citation
A LOWER BOUND FOR THE GONALITY CONJECTURE
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2017, pp. 561-563
-
- Article
- Export citation
LARGE MOMENTS AND EXTREME VALUES OF CLASS NUMBERS OF INDEFINITE BINARY QUADRATIC FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 20 April 2017, pp. 564-586
-
- Article
- Export citation
A NOTE ON BADLY APPROXIMABLE LINEAR FORMS ON MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2017, pp. 587-601
-
- Article
-
- You have access
- HTML
- Export citation
RANDOM MULTIPLICATIVE WALKS ON THE RESIDUES MODULO
 $n$
$n$
- Part of:
-
- Published online by Cambridge University Press:
- 12 May 2017, pp. 602-621
-
- Article
- Export citation
A POLYNOMIAL ANALOGUE OF LANDAU’S THEOREM AND RELATED PROBLEMS
- Part of:
-
- Published online by Cambridge University Press:
- 05 June 2017, pp. 622-665
-
- Article
- Export citation
ZEROS OF CERTAIN COMBINATIONS OF EISENSTEIN SERIES
- Part of:
-
- Published online by Cambridge University Press:
- 10 August 2017, pp. 666-695
-
- Article
- Export citation
ARRANGEMENTS OF HOMOTHETS OF A CONVEX BODY
- Part of:
-
- Published online by Cambridge University Press:
- 09 August 2017, pp. 696-710
-
- Article
- Export citation