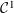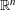1 Introduction
In [Reference Khintchine17] Khintchine proved that there exists an absolute constant
![]() $\unicode[STIX]{x1D6FE}>0$
such that for any
$\unicode[STIX]{x1D6FE}>0$
such that for any
![]() $\unicode[STIX]{x1D703}\in \mathbb{R}$
there exists
$\unicode[STIX]{x1D703}\in \mathbb{R}$
there exists
![]() $x\in \mathbb{R}$
satisfying
$x\in \mathbb{R}$
satisfying
The best known value of
![]() $\unicode[STIX]{x1D6FE}$
is probably due to Godwin [Reference Godwin13]. More than 50 years later, Tseng [Reference Tseng28] showed that, for every
$\unicode[STIX]{x1D6FE}$
is probably due to Godwin [Reference Godwin13]. More than 50 years later, Tseng [Reference Tseng28] showed that, for every
![]() $\unicode[STIX]{x1D703}\in \mathbb{R}$
, the set of all
$\unicode[STIX]{x1D703}\in \mathbb{R}$
, the set of all
![]() $x$
for which there exists a positive constant
$x$
for which there exists a positive constant
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D703},x)$
such that (1) is true is
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D703},x)$
such that (1) is true is
![]() $1/8$
-winning for the standard Schmidt game (in particular, it has maximal Hausdorff dimension). Now we usually refer to such sets, denoted by
$1/8$
-winning for the standard Schmidt game (in particular, it has maximal Hausdorff dimension). Now we usually refer to such sets, denoted by
![]() $\text{Bad}_{\unicode[STIX]{x1D703}}$
, as sets of twisted badly approximable numbers.
$\text{Bad}_{\unicode[STIX]{x1D703}}$
, as sets of twisted badly approximable numbers.
In the other direction, Kim [Reference Kim20] proved that
![]() $\text{Bad}_{\unicode[STIX]{x1D703}}$
has zero Lebesgue measure if
$\text{Bad}_{\unicode[STIX]{x1D703}}$
has zero Lebesgue measure if
![]() $\unicode[STIX]{x1D703}\in \mathbb{R}\setminus \mathbb{Q}$
.
$\unicode[STIX]{x1D703}\in \mathbb{R}\setminus \mathbb{Q}$
.
The study of twisted badly approximable numbers has been pursued to higher dimension as the classical approximation by rationals. Various multidimensional generalizations of Khinchine’s result were due to Khinchine [Reference Khintchine18, Reference Khintchine19], Jarník [Reference Jarník15, Reference Jarník16], Kleinbock [Reference Kleinbock21], Bugeaud et al [Reference Bugeaud, Harrap, Kristensen and Velani7], Moschevitin [Reference Moshchevitin22], Einsiedler and Tseng [Reference Einsiedler and Tseng10] and others. In the classical case, Schmidt introduced the weighted simultaneously badly approximable numbers
where
![]() $i,j$
are real positive numbers satisfying
$i,j$
are real positive numbers satisfying
![]() $i+j=1$
.
$i+j=1$
.
It is well-known that
![]() $\text{Bad}(i,j)$
has Lebesgue measure 0 and it was shown to have full Hausdorff dimension by Pollington and Velani [Reference Pollington and Velani23] only in 2002. A few years later, Badziahin, Pollington and Velani made a breakthrough [Reference Badziahin, Pollington and Velani3] by settling a famous conjecture of Schmidt. They proved that any countable intersection with a certain restriction of sets
$\text{Bad}(i,j)$
has Lebesgue measure 0 and it was shown to have full Hausdorff dimension by Pollington and Velani [Reference Pollington and Velani23] only in 2002. A few years later, Badziahin, Pollington and Velani made a breakthrough [Reference Badziahin, Pollington and Velani3] by settling a famous conjecture of Schmidt. They proved that any countable intersection with a certain restriction of sets
![]() $\text{Bad}(i,j)$
for different weights
$\text{Bad}(i,j)$
for different weights
![]() $(i,j)$
has full Hausdorff dimension. This result was significantly improved by An in [Reference An1], where he proved that
$(i,j)$
has full Hausdorff dimension. This result was significantly improved by An in [Reference An1], where he proved that
![]() $\text{Bad}(i,j)$
is winning for the standard Schmidt game and thus obtained the full dimension result for countable intersections unconditionally.
$\text{Bad}(i,j)$
is winning for the standard Schmidt game and thus obtained the full dimension result for countable intersections unconditionally.
Moreover, Badziahin, Pollington and Velani’s work settled the foundations for the study of the dimension of
![]() $\text{Bad}(i,j)$
on planar curves. In 1964, Davenport asked the question: is the intersection of
$\text{Bad}(i,j)$
on planar curves. In 1964, Davenport asked the question: is the intersection of
![]() $\text{Bad}(1/2,1/2)$
with the parabola uncountable? Badziahin and Velani [Reference Badziahin and Velani4] answered this question positively and proved the more general result: the set
$\text{Bad}(1/2,1/2)$
with the parabola uncountable? Badziahin and Velani [Reference Badziahin and Velani4] answered this question positively and proved the more general result: the set
![]() $\text{Bad}(i,j)$
on any
$\text{Bad}(i,j)$
on any
![]() $C^{(2)}$
non-degenerate planar curve has full dimension. This is false in general if we replace non-degenerate curves by straight lines. Recently, Badziahin and Velani’s result has been improved to winning in [Reference An, Beresnevich and Velani2] and generalized to higher dimension by Beresnevich [Reference Beresnevich6]. In higher dimension, we fix an
$C^{(2)}$
non-degenerate planar curve has full dimension. This is false in general if we replace non-degenerate curves by straight lines. Recently, Badziahin and Velani’s result has been improved to winning in [Reference An, Beresnevich and Velani2] and generalized to higher dimension by Beresnevich [Reference Beresnevich6]. In higher dimension, we fix an
![]() $n$
-tuple
$n$
-tuple
![]() $\boldsymbol{k}=(k_{1},\ldots ,k_{n})$
of real numbers satisfying
$\boldsymbol{k}=(k_{1},\ldots ,k_{n})$
of real numbers satisfying
and define
Here,
![]() $|\cdot |$
denotes the supremum norm,
$|\cdot |$
denotes the supremum norm,
![]() $\unicode[STIX]{x1D6E9}=(\unicode[STIX]{x1D6E9}_{ij})$
and
$\unicode[STIX]{x1D6E9}=(\unicode[STIX]{x1D6E9}_{ij})$
and
![]() $\unicode[STIX]{x1D6E9}_{i}(q)$
is the product of the
$\unicode[STIX]{x1D6E9}_{i}(q)$
is the product of the
![]() $i$
th line of
$i$
th line of
![]() $\unicode[STIX]{x1D6E9}$
with the vector
$\unicode[STIX]{x1D6E9}$
with the vector
![]() $q$
, i.e.
$q$
, i.e.
Beresnevich proved that any countable intersection with a certain restriction of sets
![]() $\text{Bad}(\boldsymbol{k},n,1)$
for different weights
$\text{Bad}(\boldsymbol{k},n,1)$
for different weights
![]() $\boldsymbol{k}$
(and same dimension of approximation
$\boldsymbol{k}$
(and same dimension of approximation
![]() $n\times 1$
) with any analytic non-degenerate manifold in
$n\times 1$
) with any analytic non-degenerate manifold in
![]() $\mathbb{R}^{n}$
has full dimension. Thus, he also settled a generalization to higher dimension of Schmidt’s conjecture.
$\mathbb{R}^{n}$
has full dimension. Thus, he also settled a generalization to higher dimension of Schmidt’s conjecture.
In twisted Diophantine approximation, much less is known. Given
![]() $\unicode[STIX]{x1D6E9}\in \text{Mat}_{n\times m}(\mathbb{R})$
, we define
$\unicode[STIX]{x1D6E9}\in \text{Mat}_{n\times m}(\mathbb{R})$
, we define
The Lebesgue measure of
![]() $\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,1)$
is zero for almost all
$\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,1)$
is zero for almost all
![]() $\unicode[STIX]{x1D6E9}\in \mathbb{R}^{n}$
and its Hausdorff dimension is always maximal (see [Reference Bengoechea and Moshchevitin5]). The winning property in
$\unicode[STIX]{x1D6E9}\in \mathbb{R}^{n}$
and its Hausdorff dimension is always maximal (see [Reference Bengoechea and Moshchevitin5]). The winning property in
![]() $n\times m$
dimension has been proved by Harrap and Moshchevitin [Reference Harrap and Moshchevitin14] provided that
$n\times m$
dimension has been proved by Harrap and Moshchevitin [Reference Harrap and Moshchevitin14] provided that
![]() $\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
. The general problem remains open even for
$\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
. The general problem remains open even for
![]() $n=2,~m=1$
.
$n=2,~m=1$
.
In this note, we keep the condition
![]() $\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
and study the Hausdorff dimension and winning property of
$\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
and study the Hausdorff dimension and winning property of
![]() $\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)$
on manifolds of
$\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)$
on manifolds of
![]() $\mathbb{R}^{n}$
.
$\mathbb{R}^{n}$
.
2 Statement and discussion of results
There are different definitions for a set to be winning in a Euclidean space
![]() ${\mathcal{E}}$
. In this paper we consider classical Schmidt’s definition. So when we say that a set is winning in the Euclidean space
${\mathcal{E}}$
. In this paper we consider classical Schmidt’s definition. So when we say that a set is winning in the Euclidean space
![]() ${\mathcal{E}}$
we mean that it is
${\mathcal{E}}$
we mean that it is
![]() $\unicode[STIX]{x1D6FC}$
-winning in
$\unicode[STIX]{x1D6FC}$
-winning in
![]() ${\mathcal{E}}$
for some
${\mathcal{E}}$
for some
![]() $0<\unicode[STIX]{x1D6FC}\leqslant 1/2$
in the sense of Schmidt’s game [Reference Schmidt24–Reference Schmidt26]. One of the reasons is that we apply a lemma from [Reference Moshchevitin22] that was formulated for classical Schmidt’s games. However, it is clear that Theorems 2.1 and 2.4 will be true for the hyperplane absolute game (for the definition see [Reference Fishman, Simmons and Urbański11]).
$0<\unicode[STIX]{x1D6FC}\leqslant 1/2$
in the sense of Schmidt’s game [Reference Schmidt24–Reference Schmidt26]. One of the reasons is that we apply a lemma from [Reference Moshchevitin22] that was formulated for classical Schmidt’s games. However, it is clear that Theorems 2.1 and 2.4 will be true for the hyperplane absolute game (for the definition see [Reference Fishman, Simmons and Urbański11]).
A
![]() $C^{(1)}$
curve
$C^{(1)}$
curve
![]() ${\mathcal{C}}$
in
${\mathcal{C}}$
in
![]() $\mathbb{R}^{n}$
can be written in the form
$\mathbb{R}^{n}$
can be written in the form
where
![]() $f=(f_{1},\ldots ,f_{n}):I\rightarrow \mathbb{R}^{n}$
is a
$f=(f_{1},\ldots ,f_{n}):I\rightarrow \mathbb{R}^{n}$
is a
![]() $C^{(1)}$
map defined on a compact interval
$C^{(1)}$
map defined on a compact interval
![]() $I\subset \mathbb{R}$
. We call
$I\subset \mathbb{R}$
. We call
![]() ${\mathcal{C}}$
non-degenerate (respectively, everywhere non-degenerate) if for all
${\mathcal{C}}$
non-degenerate (respectively, everywhere non-degenerate) if for all
![]() $i=1,\ldots ,n$
we have
$i=1,\ldots ,n$
we have
![]() $f_{i}^{\prime }(x)\neq 0$
for some
$f_{i}^{\prime }(x)\neq 0$
for some
![]() $x\in I$
(respectively, for all
$x\in I$
(respectively, for all
![]() $x\in I$
). We call a
$x\in I$
). We call a
![]() $C^{(1)}$
submanifold of
$C^{(1)}$
submanifold of
![]() $\mathbb{R}^{n}$
non-degenerate if it can be foliated by non-degenerate
$\mathbb{R}^{n}$
non-degenerate if it can be foliated by non-degenerate
![]() $C^{(1)}$
curves.
$C^{(1)}$
curves.
Theorem 2.1. Let
![]() $\boldsymbol{k}=(k_{1},\ldots ,k_{n})$
be an
$\boldsymbol{k}=(k_{1},\ldots ,k_{n})$
be an
![]() $n$
-tuple of positive real numbers satisfying
$n$
-tuple of positive real numbers satisfying
![]() $\sum _{i=1}^{n}k_{i}=1$
. Let
$\sum _{i=1}^{n}k_{i}=1$
. Let
![]() $\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
and
$\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
and
![]() ${\mathcal{C}}\subset \mathbb{R}^{n}$
be an everywhere non-degenerate
${\mathcal{C}}\subset \mathbb{R}^{n}$
be an everywhere non-degenerate
![]() $C^{(1)}$
curve. Then the set
$C^{(1)}$
curve. Then the set
![]() $\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)\cap {\mathcal{C}}$
is winning.
$\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)\cap {\mathcal{C}}$
is winning.
In view of the fact that the intersection of countably many winning sets is winning and that a winning set has full dimension, given any countable collection
![]() $(\boldsymbol{k}_{t})_{t\geqslant 1}$
of
$(\boldsymbol{k}_{t})_{t\geqslant 1}$
of
![]() $n$
-tuples
$n$
-tuples
![]() $\boldsymbol{k}_{t}=(k_{1,t},\ldots ,k_{n,t})$
of positive real numbers satisfying
$\boldsymbol{k}_{t}=(k_{1,t},\ldots ,k_{n,t})$
of positive real numbers satisfying
![]() $\sum _{i=1}^{n}k_{i,t}=1$
, Theorem 2.1 implies that
$\sum _{i=1}^{n}k_{i,t}=1$
, Theorem 2.1 implies that
for any
![]() $\unicode[STIX]{x1D6E9}\in \bigcap _{t\geqslant 1}\text{Bad}(\boldsymbol{k}_{t},n,m)$
and any everywhere non-degenerate
$\unicode[STIX]{x1D6E9}\in \bigcap _{t\geqslant 1}\text{Bad}(\boldsymbol{k}_{t},n,m)$
and any everywhere non-degenerate
![]() $C^{(1)}$
curve
$C^{(1)}$
curve
![]() ${\mathcal{C}}\subset \mathbb{R}^{n}$
. If we require that
${\mathcal{C}}\subset \mathbb{R}^{n}$
. If we require that
![]() ${\mathcal{C}}$
is non-degenerate only for some
${\mathcal{C}}$
is non-degenerate only for some
![]() $x\in I$
instead of everywhere, we can still choose an interval
$x\in I$
instead of everywhere, we can still choose an interval
![]() $I_{0}\subset I$
small enough so that the shorter curve
$I_{0}\subset I$
small enough so that the shorter curve
![]() ${\mathcal{C}}^{\ast }=\{(f_{1}(x),\ldots ,f_{n}(x)),~x\in I_{0}\}$
clearly is everywhere non-degenerate. Then we have equation (4) for
${\mathcal{C}}^{\ast }=\{(f_{1}(x),\ldots ,f_{n}(x)),~x\in I_{0}\}$
clearly is everywhere non-degenerate. Then we have equation (4) for
![]() ${\mathcal{C}}^{\ast }$
and of course also for
${\mathcal{C}}^{\ast }$
and of course also for
![]() $C$
. The fibering technique (see [Reference Sprindzuk27, pp. 9–10] and [Reference Beresnevich6, §2.1]) establishes the generalization of (4) to non-degenerate
$C$
. The fibering technique (see [Reference Sprindzuk27, pp. 9–10] and [Reference Beresnevich6, §2.1]) establishes the generalization of (4) to non-degenerate
![]() $C^{(1)}$
manifolds.
$C^{(1)}$
manifolds.
Corollary 2.2. Let
![]() $(\boldsymbol{k}_{t})_{t\geqslant 1}$
be a countable collection of
$(\boldsymbol{k}_{t})_{t\geqslant 1}$
be a countable collection of
![]() $n$
-tuples
$n$
-tuples
![]() $\boldsymbol{k}_{t}=(k_{1,t},\ldots ,k_{n,t})$
of positive real numbers satisfying
$\boldsymbol{k}_{t}=(k_{1,t},\ldots ,k_{n,t})$
of positive real numbers satisfying
![]() $\sum _{i=1}^{n}k_{i,t}=1$
. Let
$\sum _{i=1}^{n}k_{i,t}=1$
. Let
![]() $\unicode[STIX]{x1D6E9}\in \bigcap _{t\geqslant 1}\text{Bad}(\boldsymbol{k}_{t},n,m)$
and
$\unicode[STIX]{x1D6E9}\in \bigcap _{t\geqslant 1}\text{Bad}(\boldsymbol{k}_{t},n,m)$
and
![]() ${\mathcal{M}}\subset \mathbb{R}^{n}$
be a non-degenerate
${\mathcal{M}}\subset \mathbb{R}^{n}$
be a non-degenerate
![]() $C^{(1)}$
manifold. Then
$C^{(1)}$
manifold. Then
The proofs of Theorem 2.1 and Corollary 2.2 are given in §3. The arguments used there do not provide winning on everywhere non-degenerate
![]() $C^{(1)}$
manifolds unless the manifold is a curve. However, a different strategy can be adopted to prove winning on affine subspaces.
$C^{(1)}$
manifolds unless the manifold is a curve. However, a different strategy can be adopted to prove winning on affine subspaces.
Definition 2.3. We call a set
![]() ${\mathcal{N}}\subset \mathbb{R}^{n}$
isotropically winning if for each
${\mathcal{N}}\subset \mathbb{R}^{n}$
isotropically winning if for each
![]() $d\leqslant n$
and for each
$d\leqslant n$
and for each
![]() $d$
-dimensional affine subspace
$d$
-dimensional affine subspace
![]() ${\mathcal{A}}\subset \mathbb{R}^{n}$
the intersection
${\mathcal{A}}\subset \mathbb{R}^{n}$
the intersection
![]() ${\mathcal{N}}\cap {\mathcal{A}}$
is
${\mathcal{N}}\cap {\mathcal{A}}$
is
![]() $1/2$
-winning.
$1/2$
-winning.
Here we should note that the isotropically winning property is really a very strong property. For example, the set
![]() $\text{Bad}(1/2,1/2)$
is
$\text{Bad}(1/2,1/2)$
is
![]() $1/2$
-winning in Schmidt’s sense, however it is not isotropically winning.
$1/2$
-winning in Schmidt’s sense, however it is not isotropically winning.
Theorem 2.4. If
![]() $\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
, then
$\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
, then
![]() $\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)$
is isotropically winning.
$\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)$
is isotropically winning.
Section 4 is devoted to the proof of Theorem 2.4. We give an outline of the proof in §4.1.
3 Proof of Theorem 2.1
Let
![]() ${\mathcal{C}}\subset \mathbb{R}^{n}$
be an everywhere non-degenerate
${\mathcal{C}}\subset \mathbb{R}^{n}$
be an everywhere non-degenerate
![]() $C^{(1)}$
curve as in (3). Let
$C^{(1)}$
curve as in (3). Let
![]() $\boldsymbol{k}=(k_{1},\ldots ,k_{n})$
be an
$\boldsymbol{k}=(k_{1},\ldots ,k_{n})$
be an
![]() $n$
-tuple of real numbers satisfying (2). Without loss of generality assume that
$n$
-tuple of real numbers satisfying (2). Without loss of generality assume that
![]() $k_{1}=\max _{1\leqslant i\leqslant n}(k_{i})$
. Let
$k_{1}=\max _{1\leqslant i\leqslant n}(k_{i})$
. Let
![]() $\unicode[STIX]{x1D70B}:\mathbb{R}^{n}\rightarrow \mathbb{R}$
be the projection map onto the first coordinate.
$\unicode[STIX]{x1D70B}:\mathbb{R}^{n}\rightarrow \mathbb{R}$
be the projection map onto the first coordinate.
Theorem 3.1. If
![]() $\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
, the set
$\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
, the set
![]() $\unicode[STIX]{x1D70B}(\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)\cap {\mathcal{C}})$
is
$\unicode[STIX]{x1D70B}(\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)\cap {\mathcal{C}})$
is
![]() $1/4$
-winning.
$1/4$
-winning.
If
![]() $\max _{1\leqslant i\leqslant n}(k_{i})=k_{t}\neq k_{1}$
, then we consider the projection onto the
$\max _{1\leqslant i\leqslant n}(k_{i})=k_{t}\neq k_{1}$
, then we consider the projection onto the
![]() $t$
th coordinate rather than the first.
$t$
th coordinate rather than the first.
Since
![]() $f_{i}^{\prime }(x)\neq 0$
for all
$f_{i}^{\prime }(x)\neq 0$
for all
![]() $x\in I$
by hypothesis, the projection map
$x\in I$
by hypothesis, the projection map
![]() $\unicode[STIX]{x1D70B}$
is bi-Lipschitz on
$\unicode[STIX]{x1D70B}$
is bi-Lipschitz on
![]() ${\mathcal{C}}$
. Now the image of a winning set under a bi-Lipschitz map is again winning (see [Reference Dani9, Proposition 5.3]), so Theorem 2.1 follows from Theorem 3.1.
${\mathcal{C}}$
. Now the image of a winning set under a bi-Lipschitz map is again winning (see [Reference Dani9, Proposition 5.3]), so Theorem 2.1 follows from Theorem 3.1.
Proof. Since
![]() $f_{1}^{\prime }(x)\neq 0$
for all
$f_{1}^{\prime }(x)\neq 0$
for all
![]() $x\in I$
, the function
$x\in I$
, the function
![]() $f_{1}$
is monotone on
$f_{1}$
is monotone on
![]() $I$
, so there exists a constant
$I$
, so there exists a constant
![]() $\unicode[STIX]{x1D705}\geqslant 1$
such that
$\unicode[STIX]{x1D705}\geqslant 1$
such that
for all
![]() $x,x^{\prime }\in I$
.
$x,x^{\prime }\in I$
.
Since
![]() $\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
, there exists a constant
$\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
, there exists a constant
![]() $0<c<1$
satisfying
$0<c<1$
satisfying
Alice and Bob play a Schmidt game on the interval
![]() $f_{1}(I)$
. A Schmidt game involves two real numbers
$f_{1}(I)$
. A Schmidt game involves two real numbers
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in (0,1)$
and starts with Bob choosing a closed interval
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in (0,1)$
and starts with Bob choosing a closed interval
![]() $B_{0}\subset f_{1}(I)$
. Next, Alice chooses a closed interval
$B_{0}\subset f_{1}(I)$
. Next, Alice chooses a closed interval
![]() $A_{0}\subset B_{0}$
of length
$A_{0}\subset B_{0}$
of length
![]() $\unicode[STIX]{x1D6FC}|B_{0}|$
. Then, Bob chooses at will a closed interval
$\unicode[STIX]{x1D6FC}|B_{0}|$
. Then, Bob chooses at will a closed interval
![]() $B_{1}\subset A_{0}$
of length
$B_{1}\subset A_{0}$
of length
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}|B_{0}|$
. Alice and Bob keep playing alternately in this way, generating a nested sequence of closed intervals in
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}|B_{0}|$
. Alice and Bob keep playing alternately in this way, generating a nested sequence of closed intervals in
![]() $f_{1}(I)$
:
$f_{1}(I)$
:
with lengths
The subset
![]() $\unicode[STIX]{x1D70B}(\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)\cap {\mathcal{C}})$
is called
$\unicode[STIX]{x1D70B}(\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)\cap {\mathcal{C}})$
is called
![]() $\unicode[STIX]{x1D6FC}$
-winning if Alice can play so that the unique point of intersection
$\unicode[STIX]{x1D6FC}$
-winning if Alice can play so that the unique point of intersection
lies in
![]() $\unicode[STIX]{x1D70B}(\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)\cap {\mathcal{C}})$
whatever the value of
$\unicode[STIX]{x1D70B}(\text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)\cap {\mathcal{C}})$
whatever the value of
![]() $\unicode[STIX]{x1D6FD}$
is. The goal is to describe a
$\unicode[STIX]{x1D6FD}$
is. The goal is to describe a
![]() $1/4$
-winning strategy for Alice.
$1/4$
-winning strategy for Alice.
Suppose Bob has chosen a closed interval
![]() $B_{0}\subset f_{1}(I)$
. We can assume
$B_{0}\subset f_{1}(I)$
. We can assume
![]() $|B_{0}|$
to be of length as small as we want. In particular, we assume
$|B_{0}|$
to be of length as small as we want. In particular, we assume
Let
and fix
![]() $\unicode[STIX]{x1D716}>0$
such that
$\unicode[STIX]{x1D716}>0$
such that
By the definition of the game, for each
![]() $s\geqslant 0$
,
$s\geqslant 0$
,
For each
![]() $(p,q)\in \mathbb{Z}^{n}\times \mathbb{Z}^{m}$
, let
$(p,q)\in \mathbb{Z}^{n}\times \mathbb{Z}^{m}$
, let
The interval
![]() $\unicode[STIX]{x1D6E5}(p,q)$
is the projection of the points in
$\unicode[STIX]{x1D6E5}(p,q)$
is the projection of the points in
![]() ${\mathcal{C}}$
lying in a hyperrectangle centred at
${\mathcal{C}}$
lying in a hyperrectangle centred at
![]() $(\unicode[STIX]{x1D6E9}_{1}(q)-p_{1},\ldots ,\unicode[STIX]{x1D6E9}_{n}(q)-p_{n})$
of size
$(\unicode[STIX]{x1D6E9}_{1}(q)-p_{1},\ldots ,\unicode[STIX]{x1D6E9}_{n}(q)-p_{n})$
of size
![]() $\unicode[STIX]{x1D716}|q|^{-mk_{1}}\times \cdots \times \unicode[STIX]{x1D716}|q|^{-mk_{n}}$
. Clearly,
$\unicode[STIX]{x1D716}|q|^{-mk_{1}}\times \cdots \times \unicode[STIX]{x1D716}|q|^{-mk_{n}}$
. Clearly,
We define a partition of
![]() $\mathbb{Z}^{n}\times \mathbb{Z}^{m}$
by letting
$\mathbb{Z}^{n}\times \mathbb{Z}^{m}$
by letting
We prove that, for every
![]() $s\geqslant 0$
, Alice can play such that
$s\geqslant 0$
, Alice can play such that
Thus, we will have
and this will prove the theorem.
Fact 1. For each
![]() $(p,q)\in {\mathcal{P}}_{s}$
, we have that
$(p,q)\in {\mathcal{P}}_{s}$
, we have that
Fact 2. Suppose
![]() $(p,q)$
and
$(p,q)$
and
![]() $(p^{\prime },q^{\prime })$
are two points in
$(p^{\prime },q^{\prime })$
are two points in
![]() ${\mathcal{P}}_{s}$
such that
${\mathcal{P}}_{s}$
such that
![]() $\unicode[STIX]{x1D6E5}(p,q)\cap B_{s}\neq \emptyset$
and
$\unicode[STIX]{x1D6E5}(p,q)\cap B_{s}\neq \emptyset$
and
![]() $\unicode[STIX]{x1D6E5}(p^{\prime },q^{\prime })\cap B_{s}\neq \emptyset$
, i.e. suppose that there exist
$\unicode[STIX]{x1D6E5}(p^{\prime },q^{\prime })\cap B_{s}\neq \emptyset$
, i.e. suppose that there exist
![]() $x,x^{\prime }\in I$
such that for all
$x,x^{\prime }\in I$
such that for all
![]() $i=1,\ldots ,n$
,
$i=1,\ldots ,n$
,
and
Next we show that
![]() $(p,q)=(p^{\prime },q^{\prime })$
. Indeed, the inequality (5) implies that, for all
$(p,q)=(p^{\prime },q^{\prime })$
. Indeed, the inequality (5) implies that, for all
![]() $i=1,\ldots ,n$
,
$i=1,\ldots ,n$
,
Hence,
 $$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D6E9}_{i}(q-q^{\prime })-(p_{i}-p_{i}^{\prime })| & \stackrel{(10),(9)}{{<}} & \displaystyle {\displaystyle \frac{2\unicode[STIX]{x1D716}}{R^{(s-1)mk_{i}}}}+{\displaystyle \frac{\unicode[STIX]{x1D705}|B_{0}|}{R^{smk_{1}}}}\nonumber\\ \displaystyle & \stackrel{(8),(7)}{{<}} & \displaystyle {\displaystyle \frac{c}{2R^{smk_{i}}}}+{\displaystyle \frac{c}{2R^{smk_{i}}}}\nonumber\\ \displaystyle & \stackrel{(10)}{{\leqslant}} & \displaystyle {\displaystyle \frac{c}{|q-q^{\prime }|^{mk_{i}}}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D6E9}_{i}(q-q^{\prime })-(p_{i}-p_{i}^{\prime })| & \stackrel{(10),(9)}{{<}} & \displaystyle {\displaystyle \frac{2\unicode[STIX]{x1D716}}{R^{(s-1)mk_{i}}}}+{\displaystyle \frac{\unicode[STIX]{x1D705}|B_{0}|}{R^{smk_{1}}}}\nonumber\\ \displaystyle & \stackrel{(8),(7)}{{<}} & \displaystyle {\displaystyle \frac{c}{2R^{smk_{i}}}}+{\displaystyle \frac{c}{2R^{smk_{i}}}}\nonumber\\ \displaystyle & \stackrel{(10)}{{\leqslant}} & \displaystyle {\displaystyle \frac{c}{|q-q^{\prime }|^{mk_{i}}}}\nonumber\end{eqnarray}$$
if
![]() $q\neq q^{\prime }$
. Now the condition (6) implies that the last inequality cannot hold for all
$q\neq q^{\prime }$
. Now the condition (6) implies that the last inequality cannot hold for all
![]() $i=1,\ldots ,n$
and, hence,
$i=1,\ldots ,n$
and, hence,
![]() $q=q^{\prime }$
. Then, from the second-to-last inequality it follows that, for all
$q=q^{\prime }$
. Then, from the second-to-last inequality it follows that, for all
![]() $i=1,\ldots ,n$
,
$i=1,\ldots ,n$
,
so
![]() $p_{i}=p_{i}^{\prime }$
. Thus, we conclude that
$p_{i}=p_{i}^{\prime }$
. Thus, we conclude that
![]() $p=p^{\prime }$
.
$p=p^{\prime }$
.
A straightforward consequence of the above two facts is that Alice can choose an interval
![]() $A_{s}\subset B_{s}$
of length
$A_{s}\subset B_{s}$
of length
![]() $1/4|B_{s}|$
that avoids
$1/4|B_{s}|$
that avoids
![]() $\unicode[STIX]{x1D6E5}(p,q)$
for all
$\unicode[STIX]{x1D6E5}(p,q)$
for all
![]() $(p,q)\in {\mathcal{P}}_{s}$
. This completes the proof of (11).◻
$(p,q)\in {\mathcal{P}}_{s}$
. This completes the proof of (11).◻
4 Proof of Theorem 2.4
Our exposition is organized as follows. In §4.1 we briefly explain the strategy of the proof. In §§4.2 and 4.6 we use transference arguments. In §§4.3, 4.4 and 4.5 we explore the geometry of auxiliary subspaces.
Throughout this section we denote by
![]() $|\cdot |_{e}$
the Euclidean norm.
$|\cdot |_{e}$
the Euclidean norm.
4.1 Outline of the proof
Let
![]() $1\leqslant d\leqslant n$
. Let
$1\leqslant d\leqslant n$
. Let
![]() ${\mathcal{A}}$
be a
${\mathcal{A}}$
be a
![]() $d$
-dimensional affine subspace and
$d$
-dimensional affine subspace and
![]() ${\mathcal{L}}$
be the corresponding
${\mathcal{L}}$
be the corresponding
![]() $d$
-dimensional linear subspace (so
$d$
-dimensional linear subspace (so
![]() ${\mathcal{L}}$
is the translation of
${\mathcal{L}}$
is the translation of
![]() ${\mathcal{A}}$
which contains the origin).
${\mathcal{A}}$
which contains the origin).
We briefly explain the main construction of our proof. We construct a special sequence
![]() $\unicode[STIX]{x1D6EC}$
of integer vectors
$\unicode[STIX]{x1D6EC}$
of integer vectors
![]() $\boldsymbol{u}_{r}=\boldsymbol{u}_{r}({\mathcal{L}})=(u_{r,1},\ldots ,u_{r,n})\in \mathbb{Z}^{n}$
which is useful for Khintchine’s type of inhomogeneous transference argument (see Ch. V from Cassels’s book [Reference Cassels8]). For the sequence
$\boldsymbol{u}_{r}=\boldsymbol{u}_{r}({\mathcal{L}})=(u_{r,1},\ldots ,u_{r,n})\in \mathbb{Z}^{n}$
which is useful for Khintchine’s type of inhomogeneous transference argument (see Ch. V from Cassels’s book [Reference Cassels8]). For the sequence
![]() $\unicode[STIX]{x1D6EC}$
of integer vectors
$\unicode[STIX]{x1D6EC}$
of integer vectors
![]() $\boldsymbol{u}_{r}$
we define the set
$\boldsymbol{u}_{r}$
we define the set
To establish the result of Theorem 2.4 it is enough to prove the following two facts:
Fact A. We have
![]() $N(\unicode[STIX]{x1D6EC})\subset \text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)$
.
$N(\unicode[STIX]{x1D6EC})\subset \text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)$
.
Fact B. The set
![]() $N(\unicode[STIX]{x1D6EC})$
is winning.
$N(\unicode[STIX]{x1D6EC})$
is winning.
Fact A will follow from the inhomogeneous transference argument; we give a detailed exposition in §4.6. Fact B will follow from the construction of
![]() $\unicode[STIX]{x1D6EC}$
and from Lemma 1 from [Reference Moshchevitin22]. This lemma establishes the winning property of any set of the form
$\unicode[STIX]{x1D6EC}$
and from Lemma 1 from [Reference Moshchevitin22]. This lemma establishes the winning property of any set of the form
![]() $N(\unicode[STIX]{x1D6EC})$
in the special case when
$N(\unicode[STIX]{x1D6EC})$
in the special case when
![]() $d=n$
and so
$d=n$
and so
![]() ${\mathcal{A}}=\mathbb{R}^{n}$
, under the condition that the Euclidean norms of the elements of the sequence
${\mathcal{A}}=\mathbb{R}^{n}$
, under the condition that the Euclidean norms of the elements of the sequence
![]() $\unicode[STIX]{x1D6EC}$
are lacunary. Only a minor modification is needed to deduce the winning property for the intersection
$\unicode[STIX]{x1D6EC}$
are lacunary. Only a minor modification is needed to deduce the winning property for the intersection
![]() $N(\unicode[STIX]{x1D6EC})\cap {\mathcal{A}}$
for an arbitrary
$N(\unicode[STIX]{x1D6EC})\cap {\mathcal{A}}$
for an arbitrary
![]() $d$
-dimensional subspace
$d$
-dimensional subspace
![]() ${\mathcal{A}}\subset \mathbb{R}^{n}$
, under the condition that the Euclidean norms of the projections
${\mathcal{A}}\subset \mathbb{R}^{n}$
, under the condition that the Euclidean norms of the projections
![]() $\boldsymbol{u}_{r}^{{\mathcal{L}}}$
of
$\boldsymbol{u}_{r}^{{\mathcal{L}}}$
of
![]() $\boldsymbol{u}_{r}$
onto
$\boldsymbol{u}_{r}$
onto
![]() ${\mathcal{L}}$
are lacunary, i.e.
${\mathcal{L}}$
are lacunary, i.e.
for some
![]() $M>1$
. So, as soon as one checks condition (13) then Lemma 1 from [Reference Moshchevitin22] automatically establishes Fact B for the set
$M>1$
. So, as soon as one checks condition (13) then Lemma 1 from [Reference Moshchevitin22] automatically establishes Fact B for the set
![]() $N(\unicode[STIX]{x1D6EC})$
.
$N(\unicode[STIX]{x1D6EC})$
.
4.2 Dual setting
The condition
![]() $\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
is the key to ensuring that we are able to construct a sequence
$\unicode[STIX]{x1D6E9}\in \text{Bad}(\boldsymbol{k},n,m)$
is the key to ensuring that we are able to construct a sequence
![]() $\unicode[STIX]{x1D6EC}$
satisfying (13). That condition has the following dual reformulation (see [Reference Badziahin, Pollington and Velani3] Appendix, Theorem 6, for the proof) in terms of the transposed matrix
$\unicode[STIX]{x1D6EC}$
satisfying (13). That condition has the following dual reformulation (see [Reference Badziahin, Pollington and Velani3] Appendix, Theorem 6, for the proof) in terms of the transposed matrix
![]() $\unicode[STIX]{x1D6E9}^{\ast }$
:
$\unicode[STIX]{x1D6E9}^{\ast }$
:
for some positive constant
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6E9})$
. In the sequel we suppose everywhere that
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6E9})$
. In the sequel we suppose everywhere that
One can find generalizations of this dual reformulation in [Reference German and Evdokimov12].
4.3 Subspaces
Without loss of generality we suppose
![]() $k_{1}\geqslant \cdots \geqslant k_{n}$
. Consider the subspaces
$k_{1}\geqslant \cdots \geqslant k_{n}$
. Consider the subspaces
It is clear that
![]() $\unicode[STIX]{x1D6E4}_{i}$
is an
$\unicode[STIX]{x1D6E4}_{i}$
is an
![]() $(n-i)$
-dimensional subspace of
$(n-i)$
-dimensional subspace of
![]() $\mathbb{R}^{n}$
and
$\mathbb{R}^{n}$
and
Recall that
![]() ${\mathcal{L}}\subset \mathbb{R}^{n}$
is a
${\mathcal{L}}\subset \mathbb{R}^{n}$
is a
![]() $d$
-dimensional linear subspace. We define
$d$
-dimensional linear subspace. We define
![]() $t$
to be the minimal positive integer (
$t$
to be the minimal positive integer (
![]() $d-1\leqslant t\leqslant n-1$
) such that
$d-1\leqslant t\leqslant n-1$
) such that
Denote by
![]() $\ell _{n-t}$
the coordinate line
$\ell _{n-t}$
the coordinate line
Since
![]() ${\mathcal{L}}\subset \unicode[STIX]{x1D6E4}_{n-(t+1)}$
, the first
${\mathcal{L}}\subset \unicode[STIX]{x1D6E4}_{n-(t+1)}$
, the first
![]() $n-(t+1)$
coordinates of each point
$n-(t+1)$
coordinates of each point
![]() $\boldsymbol{x}\in {\mathcal{L}}$
vanish, so the set
$\boldsymbol{x}\in {\mathcal{L}}$
vanish, so the set
![]() $N(\unicode[STIX]{x1D6EC})$
has the form
$N(\unicode[STIX]{x1D6EC})$
has the form
Hence, when we construct the sequence
![]() $\unicode[STIX]{x1D6EC}$
satisfying (13), we only have to take into account the last
$\unicode[STIX]{x1D6EC}$
satisfying (13), we only have to take into account the last
![]() $t+1$
coordinates.
$t+1$
coordinates.
In the rest of the proof we will deal with two spaces: the
![]() $(n+m)$
-dimensional space
$(n+m)$
-dimensional space
and the
![]() $(t+1)$
-dimensional subspace
$(t+1)$
-dimensional subspace
We identify
![]() ${\mathcal{L}}$
,
${\mathcal{L}}$
,
![]() $\ell _{n-t}$
and
$\ell _{n-t}$
and
![]() $\unicode[STIX]{x1D6E4}_{n-t}$
with subspaces in
$\unicode[STIX]{x1D6E4}_{n-t}$
with subspaces in
![]() $\mathbb{R}^{t+1}$
, so when we consider the angles between them, we are just considering the angles in the
$\mathbb{R}^{t+1}$
, so when we consider the angles between them, we are just considering the angles in the
![]() $(t+1)$
-dimensional space
$(t+1)$
-dimensional space
![]() $\mathbb{R}^{t+1}$
. For a vector
$\mathbb{R}^{t+1}$
. For a vector
![]() $\boldsymbol{u}\in \mathbb{R}^{n}$
we denote by
$\boldsymbol{u}\in \mathbb{R}^{n}$
we denote by
![]() $\tilde{\boldsymbol{u}}$
its projection onto the subspace
$\tilde{\boldsymbol{u}}$
its projection onto the subspace
![]() $\mathbb{R}^{t+1}=\unicode[STIX]{x1D6E4}_{n-(t+1)}$
.
$\mathbb{R}^{t+1}=\unicode[STIX]{x1D6E4}_{n-(t+1)}$
.
For the clarity of the exposition we distinguish two cases.
Case 1. If
![]() ${\mathcal{L}}=\unicode[STIX]{x1D6E4}_{n-(t+1)}$
, then
${\mathcal{L}}=\unicode[STIX]{x1D6E4}_{n-(t+1)}$
, then
![]() $t=d-1$
and the projections
$t=d-1$
and the projections
![]() $\boldsymbol{u}_{r}^{{\mathcal{L}}}$
are just the projections
$\boldsymbol{u}_{r}^{{\mathcal{L}}}$
are just the projections
![]() $\tilde{\boldsymbol{u}}_{r}$
of
$\tilde{\boldsymbol{u}}_{r}$
of
![]() $\boldsymbol{u}_{r}$
onto
$\boldsymbol{u}_{r}$
onto
![]() $\mathbb{R}^{t+1}$
. In this case, it is enough for the property (13) to ensure that the sequence
$\mathbb{R}^{t+1}$
. In this case, it is enough for the property (13) to ensure that the sequence
![]() $|\tilde{\boldsymbol{u}}_{r}|_{e}$
is lacunary.
$|\tilde{\boldsymbol{u}}_{r}|_{e}$
is lacunary.
Case 2. If
![]() ${\mathcal{L}}\neq \unicode[STIX]{x1D6E4}_{n-(t+1)}$
, then
${\mathcal{L}}\neq \unicode[STIX]{x1D6E4}_{n-(t+1)}$
, then
![]() $t\geqslant d\geqslant 1$
. In this case, we need to consider the angle
$t\geqslant d\geqslant 1$
. In this case, we need to consider the angle
![]() $\unicode[STIX]{x1D714}=\widehat{{\mathcal{L}},\ell _{n-t}}$
between the subspace
$\unicode[STIX]{x1D714}=\widehat{{\mathcal{L}},\ell _{n-t}}$
between the subspace
![]() ${\mathcal{L}}$
and the one-dimensional
${\mathcal{L}}$
and the one-dimensional
![]() $\ell _{n-t}$
. Here the angle between subspace
$\ell _{n-t}$
. Here the angle between subspace
![]() ${\mathcal{A}}$
and one-dimensional subspace
${\mathcal{A}}$
and one-dimensional subspace
![]() $l$
is defined as
$l$
is defined as
It is clear that
![]() $\widehat{\unicode[STIX]{x1D6E4}_{n-t},\ell _{n-t}}=(\unicode[STIX]{x1D70B}/2)$
, so as
$\widehat{\unicode[STIX]{x1D6E4}_{n-t},\ell _{n-t}}=(\unicode[STIX]{x1D70B}/2)$
, so as
![]() ${\mathcal{L}}\not \subset \unicode[STIX]{x1D6E4}_{n-t}$
we have
${\mathcal{L}}\not \subset \unicode[STIX]{x1D6E4}_{n-t}$
we have
Let us consider an arbitrary vector
![]() $\boldsymbol{u}\in \mathbb{R}^{n}$
. We denote by
$\boldsymbol{u}\in \mathbb{R}^{n}$
. We denote by
![]() $\boldsymbol{u}^{{\mathcal{L}}}$
and
$\boldsymbol{u}^{{\mathcal{L}}}$
and
![]() $\tilde{\boldsymbol{u}}$
the projections onto
$\tilde{\boldsymbol{u}}$
the projections onto
![]() ${\mathcal{L}}$
and
${\mathcal{L}}$
and
![]() $\mathbb{R}^{t+1}$
, respectively. We should note that the Euclidean norms satisfy the equality
$\mathbb{R}^{t+1}$
, respectively. We should note that the Euclidean norms satisfy the equality
So to obtain the lacunarity condition (13) with a given
![]() $M>1$
for the sequence of Euclidean norms of the projections
$M>1$
for the sequence of Euclidean norms of the projections
![]() $\boldsymbol{u}_{r}^{{\mathcal{L}}}$
for a certain sequence of vectors
$\boldsymbol{u}_{r}^{{\mathcal{L}}}$
for a certain sequence of vectors
![]() $\boldsymbol{u}_{r}$
we should establish two facts.
$\boldsymbol{u}_{r}$
we should establish two facts.
Fact C. The lacunarity of the sequence
![]() $|\tilde{\boldsymbol{u}}_{r}|_{e}$
, that is
$|\tilde{\boldsymbol{u}}_{r}|_{e}$
, that is
Fact D. The additional condition
where the values
![]() $\tilde{M}$
and
$\tilde{M}$
and
![]() $\unicode[STIX]{x1D70E}$
must satisfy the inequalities
$\unicode[STIX]{x1D70E}$
must satisfy the inequalities
Indeed, suppose that
![]() $\widehat{\ell _{n-t},\tilde{\boldsymbol{u}}}<\unicode[STIX]{x1D70E}$
. Then by the definition of the angle and the triangle inequality we have
$\widehat{\ell _{n-t},\tilde{\boldsymbol{u}}}<\unicode[STIX]{x1D70E}$
. Then by the definition of the angle and the triangle inequality we have
Of course here
![]() $\tilde{\boldsymbol{u}}^{{\mathcal{L}}}=\boldsymbol{u}^{{\mathcal{L}}}$
. Analogously
$\tilde{\boldsymbol{u}}^{{\mathcal{L}}}=\boldsymbol{u}^{{\mathcal{L}}}$
. Analogously
So we have
Now from (15), (16) and (17) we deduce
and this gives (13).
Now we put
![]() $M=2$
. Then
$M=2$
. Then
![]() $\tilde{M}=(2\cos (\unicode[STIX]{x1D714}-\unicode[STIX]{x1D70E})/\text{cos}(\unicode[STIX]{x1D714}+\unicode[STIX]{x1D70E}))$
. So to obtain (15) and (17) it is enough to satisfy the condition
$\tilde{M}=(2\cos (\unicode[STIX]{x1D714}-\unicode[STIX]{x1D70E})/\text{cos}(\unicode[STIX]{x1D714}+\unicode[STIX]{x1D70E}))$
. So to obtain (15) and (17) it is enough to satisfy the condition
In the next subsection, we construct the sequence
![]() $\unicode[STIX]{x1D6EC}$
by constructing a sequence of parallelepipeds
$\unicode[STIX]{x1D6EC}$
by constructing a sequence of parallelepipeds
![]() $\unicode[STIX]{x1D6F1}_{T}$
in
$\unicode[STIX]{x1D6F1}_{T}$
in
![]() $\mathbb{R}^{n+m}$
and by choosing a certain integer vector
$\mathbb{R}^{n+m}$
and by choosing a certain integer vector
![]() $\boldsymbol{u}_{r}$
in each of them. To ensure (16), we construct the corresponding parallelepipeds
$\boldsymbol{u}_{r}$
in each of them. To ensure (16), we construct the corresponding parallelepipeds
![]() $\overline{\unicode[STIX]{x1D6F1}}_{T}$
in
$\overline{\unicode[STIX]{x1D6F1}}_{T}$
in
![]() $\mathbb{R}^{t+1}$
very long in the
$\mathbb{R}^{t+1}$
very long in the
![]() $n-t$
direction and short in the other directions corresponding to
$n-t$
direction and short in the other directions corresponding to
![]() $n-t+j,1\leqslant j\leqslant t$
. (The precise definitions will be given in the next subsection.) Hence, the vectors
$n-t+j,1\leqslant j\leqslant t$
. (The precise definitions will be given in the next subsection.) Hence, the vectors
![]() $\boldsymbol{u}_{r}$
we choose in each parallelepiped are close to the line
$\boldsymbol{u}_{r}$
we choose in each parallelepiped are close to the line
![]() $\ell _{n-t}$
and their projections onto
$\ell _{n-t}$
and their projections onto
![]() ${\mathcal{L}}$
are close to the line
${\mathcal{L}}$
are close to the line
![]() $\ell _{n-t}^{{\mathcal{L}}}$
.
$\ell _{n-t}^{{\mathcal{L}}}$
.
4.4 Parallelepipeds
First of all we put
Then
For
![]() $t\geqslant 1$
we define
$t\geqslant 1$
we define
We proceed now to the construction of the sequence
![]() $\unicode[STIX]{x1D6EC}$
. Given
$\unicode[STIX]{x1D6EC}$
. Given
![]() $T\geqslant ~1$
and a collection of strictly positive real numbers
$T\geqslant ~1$
and a collection of strictly positive real numbers
![]() $\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{n+1}$
, we consider the
$\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{n+1}$
, we consider the
![]() $(n+m)$
-dimensional parallelepiped
$(n+m)$
-dimensional parallelepiped
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{T}(\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{n+1}) & = & \displaystyle \Bigl\{(\boldsymbol{x},\boldsymbol{y})\in \mathbb{R}^{n}\times \mathbb{R}^{m}:\,|x_{i}|\leqslant \unicode[STIX]{x1D6FD}_{i}T^{mk_{i}}~(1\leqslant i\leqslant n),\nonumber\\ \displaystyle & & \displaystyle \quad \!\max _{1\leqslant j\leqslant m}|\unicode[STIX]{x1D6E9}_{j}^{\ast }(x)-y_{j}|\leqslant \unicode[STIX]{x1D6FD}_{n+1}T^{-1}\Bigr\}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{T}(\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{n+1}) & = & \displaystyle \Bigl\{(\boldsymbol{x},\boldsymbol{y})\in \mathbb{R}^{n}\times \mathbb{R}^{m}:\,|x_{i}|\leqslant \unicode[STIX]{x1D6FD}_{i}T^{mk_{i}}~(1\leqslant i\leqslant n),\nonumber\\ \displaystyle & & \displaystyle \quad \!\max _{1\leqslant j\leqslant m}|\unicode[STIX]{x1D6E9}_{j}^{\ast }(x)-y_{j}|\leqslant \unicode[STIX]{x1D6FD}_{n+1}T^{-1}\Bigr\}\nonumber\end{eqnarray}$$
and its projection onto
![]() $\mathbb{R}^{t+1}$
$\mathbb{R}^{t+1}$
By (14) we have
As
![]() $\unicode[STIX]{x1D706}>1$
we have
$\unicode[STIX]{x1D706}>1$
we have
However, the parallelepiped
is convex, symmetric, with volume
and then, by Minkowski’s convex body theorem, we have
Therefore, for each
![]() $T\geqslant 1$
there exists at least one integer vector
$T\geqslant 1$
there exists at least one integer vector
![]() $\boldsymbol{w}=(\boldsymbol{u},\boldsymbol{v})\in \mathbb{Z}^{n+m}$
such that
$\boldsymbol{w}=(\boldsymbol{u},\boldsymbol{v})\in \mathbb{Z}^{n+m}$
such that
Among these integer vectors we choose one with the smallest coordinate
![]() $|u_{n-t}|\geqslant 1$
. If this vector is not unique we choose that for which
$|u_{n-t}|\geqslant 1$
. If this vector is not unique we choose that for which
![]() $\max _{1\leqslant j\leqslant m}|\unicode[STIX]{x1D6E9}_{j}^{\ast }(\boldsymbol{u})-v_{j}|$
attains its minimal value. We denote this vector by
$\max _{1\leqslant j\leqslant m}|\unicode[STIX]{x1D6E9}_{j}^{\ast }(\boldsymbol{u})-v_{j}|$
attains its minimal value. We denote this vector by
and define
Since
![]() $\boldsymbol{w}(T)\in \unicode[STIX]{x1D6F1}_{T}(\underbrace{1,\ldots ,1}_{n-t-1},\unicode[STIX]{x1D6FE}^{-m}\unicode[STIX]{x1D706}^{t},\unicode[STIX]{x1D706}^{-1},\ldots ,\unicode[STIX]{x1D706}^{-1},\unicode[STIX]{x1D6FE})$
, one has
$\boldsymbol{w}(T)\in \unicode[STIX]{x1D6F1}_{T}(\underbrace{1,\ldots ,1}_{n-t-1},\unicode[STIX]{x1D6FE}^{-m}\unicode[STIX]{x1D706}^{t},\unicode[STIX]{x1D706}^{-1},\ldots ,\unicode[STIX]{x1D706}^{-1},\unicode[STIX]{x1D6FE})$
, one has
Also we have
Since
![]() $\boldsymbol{w}\notin \unicode[STIX]{x1D6F1}_{T}(\underbrace{1,\ldots ,1}_{n-t},\underbrace{\unicode[STIX]{x1D706}^{-1},\ldots ,\unicode[STIX]{x1D706}^{-1}}_{t},\unicode[STIX]{x1D6FE})$
, it is clear that
$\boldsymbol{w}\notin \unicode[STIX]{x1D6F1}_{T}(\underbrace{1,\ldots ,1}_{n-t},\underbrace{\unicode[STIX]{x1D706}^{-1},\ldots ,\unicode[STIX]{x1D706}^{-1}}_{t},\unicode[STIX]{x1D6FE})$
, it is clear that
and so
From the definition (19), conditions (23) and (25), and the condition
![]() $k_{j}\geqslant k_{j+1}$
for
$k_{j}\geqslant k_{j+1}$
for
![]() $n-t\leqslant j\leqslant n$
we have
$n-t\leqslant j\leqslant n$
we have
and
 $$\begin{eqnarray}\displaystyle \widehat{\tilde{\boldsymbol{u}}(T),\ell _{n-t}} & {\leqslant} & \displaystyle \arctan \biggl(\frac{\sqrt{t}\max _{n-t+1\leqslant i\leqslant n}\unicode[STIX]{x1D706}^{-1}T^{mk_{i}}}{T^{mk_{n-t}}}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \arctan \biggl(\frac{\sqrt{t}}{\unicode[STIX]{x1D706}}\biggr)=\unicode[STIX]{x1D70E}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\tilde{\boldsymbol{u}}(T),\ell _{n-t}} & {\leqslant} & \displaystyle \arctan \biggl(\frac{\sqrt{t}\max _{n-t+1\leqslant i\leqslant n}\unicode[STIX]{x1D706}^{-1}T^{mk_{i}}}{T^{mk_{n-t}}}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \arctan \biggl(\frac{\sqrt{t}}{\unicode[STIX]{x1D706}}\biggr)=\unicode[STIX]{x1D70E}.\nonumber\end{eqnarray}$$
So all the constructed vectors
![]() $\boldsymbol{u}(T)$
satisfy the condition (16). Now it turns out to be sufficient to satisfy the lacunarity condition (18), for both Cases 1 and 2.
$\boldsymbol{u}(T)$
satisfy the condition (16). Now it turns out to be sufficient to satisfy the lacunarity condition (18), for both Cases 1 and 2.
4.5 Lacunarity
Let
It is clear that
We put
![]() $T=T_{r}$
and define the sequence of vectors
$T=T_{r}$
and define the sequence of vectors
![]() $\boldsymbol{u}_{r}\in \mathbb{R}^{n}$
from the equality
$\boldsymbol{u}_{r}\in \mathbb{R}^{n}$
from the equality
where
![]() $\boldsymbol{w}(\cdot )$
is defined in the previous subsection.
$\boldsymbol{w}(\cdot )$
is defined in the previous subsection.
Lemma 4.1. The sequence
![]() $|\tilde{\boldsymbol{u}}_{r}|_{e}$
satisfies the lacunarity condition (18).
$|\tilde{\boldsymbol{u}}_{r}|_{e}$
satisfies the lacunarity condition (18).
Proof. From (22) and (23) we see that
From (25) we have the lower bound
Now
by (29), and everything is proved. ◻
4.6 Application of transference identity
We now establish Fact A. Let
![]() $x\in N(\unicode[STIX]{x1D6EC})$
. So there exists a constant
$x\in N(\unicode[STIX]{x1D6EC})$
. So there exists a constant
![]() $c(x)>0$
such that
$c(x)>0$
such that
We define
For any
![]() $\boldsymbol{q}\in \mathbb{Z}_{\neq 0}^{m}$
, consider the equality
$\boldsymbol{q}\in \mathbb{Z}_{\neq 0}^{m}$
, consider the equality
It follows from the triangle inequality that
 $$\begin{eqnarray}\displaystyle c(x) & {\leqslant} & \displaystyle \Vert \mathbf{u}_{r}\cdot \boldsymbol{x}\Vert \nonumber\\ \displaystyle & {\leqslant} & \displaystyle m\max _{1\leqslant j\leqslant m}(\Vert \unicode[STIX]{x1D6E9}_{j}^{\ast }(\mathbf{u}_{r})\Vert \cdot |q_{j}|)+n\max _{1\leqslant i\leqslant n}(\Vert \unicode[STIX]{x1D6E9}_{i}(\mathbf{q})-x_{i}\Vert \cdot |u_{r,i}|)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle m\unicode[STIX]{x1D713}_{r}|\boldsymbol{q}|+n\max _{1\leqslant i\leqslant n}(\Vert \unicode[STIX]{x1D6E9}_{i}(\mathbf{q})-x_{i}\Vert \cdot |u_{r,i}|).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c(x) & {\leqslant} & \displaystyle \Vert \mathbf{u}_{r}\cdot \boldsymbol{x}\Vert \nonumber\\ \displaystyle & {\leqslant} & \displaystyle m\max _{1\leqslant j\leqslant m}(\Vert \unicode[STIX]{x1D6E9}_{j}^{\ast }(\mathbf{u}_{r})\Vert \cdot |q_{j}|)+n\max _{1\leqslant i\leqslant n}(\Vert \unicode[STIX]{x1D6E9}_{i}(\mathbf{q})-x_{i}\Vert \cdot |u_{r,i}|)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle m\unicode[STIX]{x1D713}_{r}|\boldsymbol{q}|+n\max _{1\leqslant i\leqslant n}(\Vert \unicode[STIX]{x1D6E9}_{i}(\mathbf{q})-x_{i}\Vert \cdot |u_{r,i}|).\nonumber\end{eqnarray}$$
Here we use the well-known inequality
![]() $\Vert a\boldsymbol{z}\Vert \leqslant |a|\Vert \boldsymbol{z}\Vert$
, which holds for all
$\Vert a\boldsymbol{z}\Vert \leqslant |a|\Vert \boldsymbol{z}\Vert$
, which holds for all
![]() $a\in \mathbb{R}$
and all
$a\in \mathbb{R}$
and all
![]() $\boldsymbol{z}\in \mathbb{R}^{m}$
.
$\boldsymbol{z}\in \mathbb{R}^{m}$
.
It is clear that
![]() $\unicode[STIX]{x1D713}_{r}\rightarrow 0$
as
$\unicode[STIX]{x1D713}_{r}\rightarrow 0$
as
![]() $r\rightarrow \infty$
. We show that
$r\rightarrow \infty$
. We show that
![]() $\unicode[STIX]{x1D713}_{r}$
is strictly decreasing. Indeed,
$\unicode[STIX]{x1D713}_{r}$
is strictly decreasing. Indeed,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{r}\stackrel{(27)}{{\geqslant}}\unicode[STIX]{x1D706}^{-t/mk_{n-t}}\,\unicode[STIX]{x1D6FE}^{1+1/k_{n-t}}T_{r}^{-1} & \stackrel{(29)}{=} & \displaystyle \unicode[STIX]{x1D6FE}T_{r+1}^{-1}\cdot (R\unicode[STIX]{x1D706}^{-t/mk_{n-t}}\,\unicode[STIX]{x1D6FE}^{1/k_{n-t}})\nonumber\\ \displaystyle & \stackrel{(30)}{{>}} & \displaystyle \unicode[STIX]{x1D6FE}T_{r+1}^{-1}\nonumber\\ \displaystyle & \stackrel{(24)}{{\geqslant}} & \displaystyle \unicode[STIX]{x1D713}_{r+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{r}\stackrel{(27)}{{\geqslant}}\unicode[STIX]{x1D706}^{-t/mk_{n-t}}\,\unicode[STIX]{x1D6FE}^{1+1/k_{n-t}}T_{r}^{-1} & \stackrel{(29)}{=} & \displaystyle \unicode[STIX]{x1D6FE}T_{r+1}^{-1}\cdot (R\unicode[STIX]{x1D706}^{-t/mk_{n-t}}\,\unicode[STIX]{x1D6FE}^{1/k_{n-t}})\nonumber\\ \displaystyle & \stackrel{(30)}{{>}} & \displaystyle \unicode[STIX]{x1D6FE}T_{r+1}^{-1}\nonumber\\ \displaystyle & \stackrel{(24)}{{\geqslant}} & \displaystyle \unicode[STIX]{x1D713}_{r+1}.\nonumber\end{eqnarray}$$
Moreover, from (24), (27) and (30) it follows that
Now we can choose
![]() $r$
in such a way that
$r$
in such a way that
Therefore,
and so
From (21) and (23) we deduce that
and from (22) we have
So in any case
and by (31) and the left inequality from (32),
Now from (33) and (34) we obtain
with some constant
![]() $\unicode[STIX]{x1D705}>0$
, independent of
$\unicode[STIX]{x1D705}>0$
, independent of
![]() $\boldsymbol{q}$
. Since the choice of the vector
$\boldsymbol{q}$
. Since the choice of the vector
![]() $\boldsymbol{q}$
was arbitrary, we have shown that
$\boldsymbol{q}$
was arbitrary, we have shown that
![]() $x\in \text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)$
. Hence we prove
$x\in \text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)$
. Hence we prove
![]() $N(\unicode[STIX]{x1D6EC})\subset \text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)$
.
$N(\unicode[STIX]{x1D6EC})\subset \text{Bad}_{\unicode[STIX]{x1D6E9}}(\boldsymbol{k},n,m)$
.
Acknowledgements
The first author thanks Sanju Velani and Victor Beresnevich for many educational conversations.