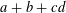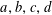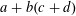Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shkredov, Ilya D.
and
Shparlinski, Igor E.
2018.
Double Character Sums with Intervals and Arbitrary Sets.
Proceedings of the Steklov Institute of Mathematics,
Vol. 303,
Issue. 1,
p.
239.
Roche-Newton, Oliver
Shparlinski, Igor E.
and
Winterhof, Arne
2019.
Analogues of the Balog–Wooley Decomposition for Subsets of Finite Fields and Character Sums with Convolutions.
Annals of Combinatorics,
Vol. 23,
Issue. 1,
p.
183.
Koh, Doowon
Mirzaei, Mozhgan
Pham, Thang
and
Shen, Chun-Yen
2020.
Exponential sum estimates over prime fields.
International Journal of Number Theory,
Vol. 16,
Issue. 02,
p.
291.