Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T05:05:13.606Z Has data issue: false hasContentIssue false
  • English
  • Français

A POLYNOMIAL ANALOGUE OF LANDAU’S THEOREM AND RELATED PROBLEMS

Part of: Multiplicative number theory

Published online by Cambridge University Press:  05 June 2017

Ofir Gorodetsky
Ofir Gorodetsky*
Affiliation:
Raymond and Beverly Sackler School of Mathematical Sciences, Tel Aviv University, P.O. Box 39040, Tel Aviv 6997801, Israel email [email protected]
Get access

Abstract

Recently, an analogue over 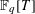$\mathbb{F}_{q}[T]$ of Landau’s theorem on sums of two squares was considered by Bary-Soroker, Smilansky and Wolf. They counted the number of monic polynomials in 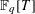$\mathbb{F}_{q}[T]$ of degree $n$ of the form 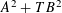$A^{2}+TB^{2}$, which we denote by 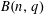$B(n,q)$. They studied 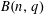$B(n,q)$ in two limits: fixed $n$ and large 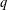$q$; and fixed 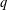$q$ and large $n$. We generalize their result to the most general limit 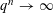$q^{n}\rightarrow \infty$. More precisely, we prove

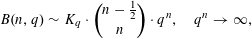$$\begin{eqnarray}B(n,q)\sim K_{q}\cdot \binom{n-\frac{1}{2}}{n}\cdot q^{n},\quad q^{n}\rightarrow \infty ,\end{eqnarray}$$
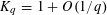for an explicit constant $K_{q}=1+O(1/q)$. Our methods are different and are based on giving explicit bounds on the coefficients of generating functions. These methods also apply to other problems, related to polynomials with prime factors of even degree.

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Mathematika , Volume 63 , Issue 2 , 2017 , pp. 622 - 665
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artin, E., Quadratische Körper im Gebiete der höheren Kongruenzen. I. Math. Z. 19(1) 1924, 153–206.Google Scholar
Bae, S. and Jung, H., On the 4-rank of ideal class groups of quadratic function fields. Acta Arith. 151(4) 2012, 325–360.Google Scholar
Bary-Soroker, L., Smilansky, Y. and Wolf, A., On the function field analogue of Landau’s theorem on sums of squares. Finite Fields Appl. 39 2016, 195–215.Google Scholar
Chevalley, C., Introduction to the Theory of Algebraic Functions of One Variable (Mathematical Surveys VI ), American Mathematical Society (New York, 1951).Google Scholar
Chuang, C.-Y., Kuan, Y.-L. and Yu, J., On counting polynomials over finite fields. Proc. Amer. Math. Soc. 143(10) 2015, 4305–4316.Google Scholar
Flajolet, P. and Sedgewick, R., Analytic Combinatorics, Cambridge University Press (Cambridge, 2009).Google Scholar
Flajolet, P. and Vardi, I., Zeta function expansions of classical constants. Unpublished manuscript, http://algo.inria.fr/flajolet/Publications/landau.ps, 1996.Google Scholar
Fouvry, É. and Klüners, J., On the negative Pell equation. Ann. of Math. (2) 172(3) 2010, 2035–2104.CrossRefGoogle Scholar
Henrici, P., Applied and Computational Complex Analysis, Vol. 2, John Wiley & Sons (New York, 1977).Google Scholar
Jameson, G. J. O., Inequalities for gamma function ratios. Amer. Math. Monthly 120(10) 2013, 936–940.Google Scholar
Knopfmacher, J., Abstract Analytic Number Theory, 2nd edn. (Dover Books on Advanced Mathematics), Dover Publications (New York, 1990).Google Scholar
Knopfmacher, J. and Zhang, W.-B., Number Theory Arising from Finite Fields (Monographs and Textbooks in Pure and Applied Mathematics 241 ), Marcel Dekker (New York, 2001).Google Scholar
Knuth, D. E. and Wilf, H. S., A short proof of Darboux’s lemma. Appl. Math. Lett. 2(2) 1989, 139–140.Google Scholar
Landau, E., Über die einteilung der positiven ganzen zahlen in vier klassen nach der mindestzahl der zu ihrer additiven zusammensetzung erforderlichen quadrate. Arch. Math. Phys. 13 1908, 305–312.Google Scholar
Leahey, W., Sums of squares of polynomials with coefficients in a finite field. Amer. Math. Monthly 74 1967, 816–819.CrossRefGoogle Scholar
Manstavičius, E. and Skrabutėnas, R., Summation of values of multiplicative functions on semigroups. Lith. Math. J. 33(3) 1993, 255–264.Google Scholar
Matei, V., A geometric perspective on Landau’s problem over function fields. Online preprint, http://www.math.wisc.edu/∼mvlad/landau.pdf, 2017.Google Scholar
Rosen, M., Number Theory in Function Fields (Graduate Texts in Mathematics 210 ), Springer (New York, 2002).Google Scholar
Shanks, D., The second-order term in the asymptotic expansion of B (x). Math. Comp. 18 1964, 75–86.Google Scholar
Shiu, D. K. L., Strings of congruent primes. J. Lond. Math. Soc. (2) 61(2) 2000, 359–373.Google Scholar
Stevenhagen, P., The number of real quadratic fields having units of negative norm. Exp. Math. 2(2) 1993, 121–136.Google Scholar
Thorne, F., Irregularities in the distributions of primes in function fields. J. Number Theory 128(6) 2008, 1784–1794.CrossRefGoogle Scholar
Wan, D., Generators and irreducible polynomials over finite fields. Math. Comp. 66(219) 1997, 1195–1212.Google Scholar
Warlimont, R., Arithmetical semigroups. V. Multiplicative functions. Manuscripta Math. 77(4) 1992, 361–383.CrossRefGoogle Scholar