Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T06:25:12.599Z Has data issue: false hasContentIssue false
  • English
  • Français

ARRANGEMENTS OF HOMOTHETS OF A CONVEX BODY

Part of: Discrete geometry General convexity Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  09 August 2017

Márton Naszódi ,
János Pach  and
Konrad Swanepoel
Márton Naszódi
Affiliation:
Department of Geometry, Lorand Eötvös University, Pazmány Péter Sétany 1/C Budapest, 1117, Hungary email [email protected]
János Pach
Affiliation:
École Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland email [email protected] Rényi Institute, Budapest, Hungary
Konrad Swanepoel
Affiliation:
Department of Mathematics, London School of Economics and Political Science, Houghton Street, London WC2A 2AE, U.K. email [email protected]
Get access

Abstract

Answering a question of Füredi and Loeb [On the best constant for the Besicovitch covering theorem. Proc. Amer. Math. Soc.121(4) (1994), 1063–1073], we show that the maximum number of pairwise intersecting homothets of a 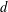$d$-dimensional centrally symmetric convex body 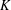$K$, none of which contains the center of another in its interior, is at most 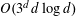$O(3^{d}d\log d)$. If 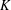$K$ is not necessarily centrally symmetric and the role of its center is played by its centroid, then the above bound can be replaced by 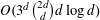$O(3^{d}\binom{2d}{d}d\log d)$. We establish analogous results for the case where the center is defined as an arbitrary point in the interior of 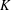$K$. We also show that, in the latter case, one can always find families of at least 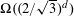$\unicode[STIX]{x1D6FA}((2/\sqrt{3})^{d})$ translates of 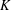$K$ with the above property.

MSC classification

Primary: 52C17: Packing and covering in $n$ dimensions
Secondary: 46B06: Asymptotic theory of Banach spaces 52A23: Asymptotic theory of convex bodies
Type
Research Article
Information
Mathematika , Volume 63 , Issue 2 , 2017 , pp. 696 - 710
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arias-de Reyna, J., Ball, K. and Villa, R., Concentration of the distance in finite-dimensional normed spaces. Mathematika 45(2) 1998, 245–252; MR 1695717.Google Scholar
Böröczky, K. and Szabó, L., Minkowski arrangements of spheres. Monatsh. Math. 141(1) 2004, 11–19; MR 2109518.CrossRefGoogle Scholar
Busemann, H., The isoperimetric problem in the Minkowski plane. Amer. J. Math. 69 1947, 863–871; MR 0023552.Google Scholar
Erdős, P. and Szekeres, G., A combinatorial problem in geometry. Compos. Math. 2 1935, 463–470; MR 1556929.Google Scholar
Fejes Tóth, L., Minkowskian distribution of discs. Proc. Amer. Math. Soc. 16 1965, 999–1004; MR 0180921.Google Scholar
Fejes Tóth, L., Minkowskian circle-aggregates. Math. Ann. 171 1967, 97–103; MR 0221386.Google Scholar
Fejes Tóth, L., Research problem. Period. Math. Hungar. 31(2) 1995, 165–166; MR 1553673.Google Scholar
Fejes Tóth, L., Minkowski circle packings on the sphere. Discrete Comput. Geom. 22(2) 1999, 161–166; MR 1698538.Google Scholar
Füredi, Z. and Loeb, P. A., On the best constant for the Besicovitch covering theorem. Proc. Amer. Math. Soc. 121(4) 1994, 1063–1073; MR 1249875 (95b:28003).Google Scholar
Grünbaum, B., Measures of symmetry for convex sets. In Convexity (Proceedings of Symposia in Pure Mathematics VII ), American Mathematical Society (Providence, RI, 1963), 233–270; MR 0156259 (27 #6187).Google Scholar
Harary, F., Jacobson, M. S., Lipman, M. J. and McMorris, F. R., Abstract sphere-of-influence graphs. Math. Comput. Modelling 17(11) 1993, 77–83; MR 1236512.CrossRefGoogle Scholar
Hatcher, A., Algebraic Topology, Cambridge University Press (Cambridge, 2002); MR 1867354 (2002k:55001).Google Scholar
Izmestiev, I., Fitting centroids by a projective transformation. Preprint, 2014, arXiv:1409.6176.Google Scholar
Malnič, A. and Mohar, B., Two results on antisocial families of balls. In Fourth Czechoslovakian Symposium on Combinatorics, Graphs and Complexity (Prachatice, 1990) (Annals of Discrete Mathematics 51 ), North-Holland (Amsterdam, 1992), 205–207; MR 1206267.CrossRefGoogle Scholar
Mel’nikov, M. S., Dependence of volume and diameter of sets in an n-dimensional Banach space. Uspehi Mat. Nauk 18(4(112)) 1963, 165–170 (Russian); MR 0156263.Google Scholar
Milman, V. D., A new proof of A. Dvoretzky’s theorem on cross-sections of convex bodies. Funkcional. Anal. i Priložen. 5(4) 1971, 28–37; MR 0293374.Google Scholar
Milman, V. D., Almost Euclidean quotient spaces of subspaces of a finite-dimensional normed space. Proc. Amer. Math. Soc. 94(3) 1985, 445–449; MR 787891 (86g:46025).Google Scholar
Milman, V. D. and Pajor, A., Entropy and asymptotic geometry of non-symmetric convex bodies. Adv. Math. 152(2) 2000, 314–335; MR 1764107 (2001e:52004).CrossRefGoogle Scholar
Milman, V. D. and Schechtman, G., Asymptotic Theory of Finite-Dimensional Normed Spaces (Lecture Notes in Mathematics 1200 ), Springer (Berlin, 1986); MR 856576.Google Scholar
Minkowski, H., Allgemeine Lehrsätze über die convexen Polyeder. Nachr. Ges. Wiss. Göttingen, Math.-Phys. Kl. 1897 1897, 198–219 (German).Google Scholar
Naszódi, M., Sandoval, L. M. and Smorodinsky, S., Bounding a global red-blue proportion using local conditions. In Proceedings of the 33rd European Workshop on Computational Geometry (EuroCG2017), Malmö University (2017), 213–217; available athttp://csconferences.mah.se/eurocg2017/proceedings.pdf.Google Scholar
Polyanskii, A., Pairwise intersecting homothets of a convex body. Discrete Math. 340 2017, 1950–1956.Google Scholar
Rogers, C. A. and Shephard, G. C., The difference body of a convex body. Arch. Math. (Basel) 8 1957, 220–233.Google Scholar
Rudelson, M., Distances between non-symmetric convex bodies and the MM ∗ -estimate. Positivity 4(2) 2000, 161–178; MR 1755679.Google Scholar
Swanepoel, K. J., Combinatorial distance geometry in normed spaces. In New Trends in Intuitive Geometry (Bolyai Society Mathematical Studies), Springer (2017); to appear, available atarXiv:1702.00066.Google Scholar
Talata, I., Exponential lower bound for the translative kissing numbers of d-dimensional convex bodies. Discrete Comput. Geom. 19(3) 1998, 447–455 (Special Issue); Dedicated to the memory of Paul Erdős. MR 98k:52046.Google Scholar
Talata, I., On Hadwiger numbers of direct products of convex bodies. In Combinatorial and Computational Geometry (Mathematical Sciences Research Institute Publications 52 ), Cambridge University Press (Cambridge, 2005), 517–528; MR 2178337 (2006g:52030).Google Scholar