Research Article
Cardinality logics. Part II: Definability in languages based on ‘exactly’
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 765-784
-
- Article
- Export citation
Addendum to “The truth is never simple”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 390-392
-
- Article
- Export citation
On parameter free induction schemas
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1082-1097
-
- Article
- Export citation
Tarski on truth and logical consequence
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 51-79
-
- Article
- Export citation
On topological spaces equivalent to ordinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 785-795
-
- Article
- Export citation
Philosophical implications of Tarski's work1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 80-91
-
- Article
- Export citation
Strong measure zero sets and rapid filters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 393-402
-
- Article
- Export citation
On the use of inaccessible numbers and order indiscernibles in lower bound arguments for random access machines
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1098-1109
-
- Article
- Export citation
Finite and finitely separable intermediate propositional logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 403-420
-
- Article
- Export citation
Degree theoretical splitting properties of recursively enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1110-1137
-
- Article
- Export citation
On the elementary theory of restricted elementary functions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 796-808
-
- Article
- Export citation
Seminormal λ-generated ideals on P κ λ
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 92-102
-
- Article
- Export citation
Backwards easton forcing and 0#
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 809-833
-
- Article
- Export citation
On the structure of semialgebraic sets over p-adic fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1138-1164
-
- Article
- Export citation
Correction to “Simple r. e. degree structures”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 103-104
-
- Article
- Export citation
Extensions séparées et immédiates de corps valués
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 421-428
-
- Article
- Export citation
Sheaves of continuous definable functions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1165-1169
-
- Article
- Export citation
A system of logic for partial functions under existence-dependent kleene equality
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 834-839
-
- Article
- Export citation
Where MA first fails
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 429-433
-
- Article
- Export citation
Equalization of finite flowers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 105-123
-
- Article
- Export citation

 for some
for some  some arithmetical
some arithmetical  and some positive
and some positive 
 with
with 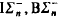 (induction and collection schemas for parameter free
(induction and collection schemas for parameter free 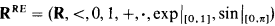
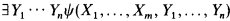
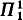 indescribable subsets of κ, then
indescribable subsets of κ, then 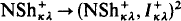 (where NSh
(where NSh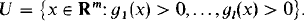
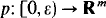
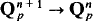 . Analytic maps are maps whose coordinate functions are given locally by convergent power series.
. Analytic maps are maps whose coordinate functions are given locally by convergent power series.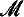 ⊨ “
⊨ “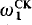 -nonstandard, then
-nonstandard, then 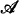 = s.p.(
= s.p.(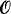 = deg{
= deg{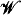 = deg{
= deg{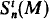 be the space of complete
be the space of complete 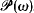 .
.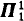 -determinacy (see a forthcoming paper by Girard and Kechris).
-determinacy (see a forthcoming paper by Girard and Kechris).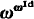 is the (smallest) equalizer for Fl
is the (smallest) equalizer for Fl