Article contents
Equalization of finite flowers
Published online by Cambridge University Press: 12 March 2014
Extract
A dilator D is a functor from ON to itself commuting with direct limits and pull-backs. A dilator D is a flower iff D(x) is continuous. A flower F is regular iff F(x) is strictly increasing and F(f)(F(z)) = F(f(z)) (for f ϵ ON(x,y), z ϵ X).
Equalization is the following axiom: if F, G ϵ Flr (class of regular flowers), then there is an H ϵ Flr such that F ° H = G ° H. From this we can deduce that if ℱ is a set ⊆ Flr, then there is an H ϵ Flr which is the smallest equalizer of ℱ (it can be said that H equalizes ℱ iff for every F, G ϵ ℱ we have F ° H = G ° H). Equalization is not provable in set theory because equalization for denumerable flowers is equivalent to 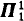 -determinacy (see a forthcoming paper by Girard and Kechris).
-determinacy (see a forthcoming paper by Girard and Kechris).
Therefore it is interesting to effectively find, by elementary means, equalizers even in the simplest cases. The aim of this paper is to prove Girard and Kechris's conjecture: “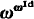 is the (smallest) equalizer for Flr < ω” (where Flr < ω denotes the set of finite regular flowers). We will verify that
is the (smallest) equalizer for Flr < ω” (where Flr < ω denotes the set of finite regular flowers). We will verify that 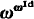 is an equalizer of Flr < ω; we will sketch the proof that it is the smallest one at the end of the paper. We will denote
is an equalizer of Flr < ω; we will sketch the proof that it is the smallest one at the end of the paper. We will denote 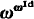 by H.
by H.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1988
References
REFERENCES
- 1
- Cited by


