Article contents
Seminormal λ-generated ideals on P κ λ
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we consider the problem of lifting properties of the Fréchet ideal Iκ = {X ⊆ κ: ∣X∣ < κ} on a regular uncountable cardinal κ, to an analogue about Iκλ , the ideal of not unbounded subsets of Pκλ. With this in mind, in §1 we introduce and study the class of seminormal λ-generated ideals on Pκλ. We shall see that ideals belonging to this class display properties which are clearly analogous to those of the Fréchet ideal on κ (for instance, with regard to saturation, normality and weak selectivity) and yet are closely related to Iκλ . Our results here show that if λ<λ = λ, then many restrictions of Iκλ are weakly selective, nowhere precipitous and, quite suprisingly, seminormal (but nowhere normal). These latter two results suggest the question of whether any restriction of Iκλ can ever be normal. In §2 we prove that if κ is strongly inaccessible, λ<κ = 2 λ and NS κλ , the ideal of nonstationary subsets of Pκλ, has a mild selective property, then NS κλ ∣A = Iκλ ∣A for some stationary A ⊆ Pκλ.
In [1] Baumgartner showed that if κ is weakly compact and P is the collection of 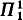 indescribable subsets of κ, then P → (P, κ)2. As a Pκλ analogue of
indescribable subsets of κ, then P → (P, κ)2. As a Pκλ analogue of 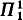 indescribability, Carr (see [3]–[5]) introduced the λ-Shelah property, but was unable to derive the natural Pκλ analogue of Baumgartner's result,
indescribability, Carr (see [3]–[5]) introduced the λ-Shelah property, but was unable to derive the natural Pκλ analogue of Baumgartner's result, 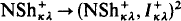 (where NSh
κλ
is the normal ideal on Pκλ induced by the λ-Shelah property). In §3 we show that the problem lies in the fact that, as far as we know, NSh
κλ
is not sufficiently distributive, and derive conditions which are sufficient and, in a sense, necessary to yield partitions related to
(where NSh
κλ
is the normal ideal on Pκλ induced by the λ-Shelah property). In §3 we show that the problem lies in the fact that, as far as we know, NSh
κλ
is not sufficiently distributive, and derive conditions which are sufficient and, in a sense, necessary to yield partitions related to 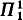 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1988
References
REFERENCES
- 3
- Cited by


