We study shear-induced migration in a dilute suspension of microswimmers (modelled as active Brownian particles or ABPs) subject to plane Poiseuille flow. For wide channels characterized by  $U_{s}/HD_{r}\ll 1$, the separation between time scales characterizing the swimmer orientation dynamics (of
$U_{s}/HD_{r}\ll 1$, the separation between time scales characterizing the swimmer orientation dynamics (of 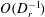 $O(D_{r}^{-1})$) and those that characterize migration across the channel (of
$O(D_{r}^{-1})$) and those that characterize migration across the channel (of  $O(H^{2}D_{r}/U_{s}^{2})$), allows for use of the method of multiple scales to derive a drift-diffusion equation for the swimmer concentration profile; here,
$O(H^{2}D_{r}/U_{s}^{2})$), allows for use of the method of multiple scales to derive a drift-diffusion equation for the swimmer concentration profile; here, 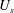 $U_{s}$ is the swimming speed,
$U_{s}$ is the swimming speed,  $H$ is the channel half-width and
$H$ is the channel half-width and 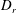 $D_{r}$ is the swimmer rotary diffusivity. The steady state concentration profile is a function of the Péclet number,
$D_{r}$ is the swimmer rotary diffusivity. The steady state concentration profile is a function of the Péclet number, 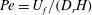 $Pe=U_{f}/(D_{r}H)$ (
$Pe=U_{f}/(D_{r}H)$ (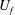 $U_{f}$ being the channel centreline velocity), and the swimmer aspect ratio
$U_{f}$ being the channel centreline velocity), and the swimmer aspect ratio  $\unicode[STIX]{x1D705}$. Swimmers with
$\unicode[STIX]{x1D705}$. Swimmers with 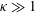 $\unicode[STIX]{x1D705}\gg 1$ (with
$\unicode[STIX]{x1D705}\gg 1$ (with 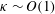 $\unicode[STIX]{x1D705}\sim O(1)$), in the regime
$\unicode[STIX]{x1D705}\sim O(1)$), in the regime 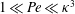 $1\ll \text{Pe}\ll \unicode[STIX]{x1D705}^{3}$ (
$1\ll \text{Pe}\ll \unicode[STIX]{x1D705}^{3}$ ( $Pe\sim O(1)$), migrate towards the channel walls, corresponding to a high-shear trapping behaviour. For
$Pe\sim O(1)$), migrate towards the channel walls, corresponding to a high-shear trapping behaviour. For 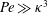 $Pe\gg \unicode[STIX]{x1D705}^{3}$ (
$Pe\gg \unicode[STIX]{x1D705}^{3}$ (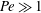 $Pe\gg 1$ for
$Pe\gg 1$ for  $\unicode[STIX]{x1D705}\sim O(1)$), however, swimmers migrate towards the centreline, corresponding to a low-shear trapping behaviour. Interestingly, within the low-shear trapping regime, swimmers with
$\unicode[STIX]{x1D705}\sim O(1)$), however, swimmers migrate towards the centreline, corresponding to a low-shear trapping behaviour. Interestingly, within the low-shear trapping regime, swimmers with 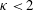 $\unicode[STIX]{x1D705}<2$ asymptote to a
$\unicode[STIX]{x1D705}<2$ asymptote to a 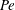 $Pe$-independent concentration profile for large
$Pe$-independent concentration profile for large 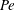 $Pe$, while those with
$Pe$, while those with 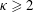 $\unicode[STIX]{x1D705}\geqslant 2$ exhibit a ‘centreline collapse’ for
$\unicode[STIX]{x1D705}\geqslant 2$ exhibit a ‘centreline collapse’ for 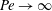 $Pe\rightarrow \infty$. The prediction of low-shear trapping, validated by Langevin simulations, is the first explanation of recent experimental observations (Barry et al., J. R. Soc. Interface, vol. 12 (112), 2015, 20150791). We organize the high-shear and low-shear trapping regimes on a
$Pe\rightarrow \infty$. The prediction of low-shear trapping, validated by Langevin simulations, is the first explanation of recent experimental observations (Barry et al., J. R. Soc. Interface, vol. 12 (112), 2015, 20150791). We organize the high-shear and low-shear trapping regimes on a 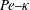 $Pe{-}\unicode[STIX]{x1D705}$ plane, thereby highlighting the singular behaviour of infinite-aspect-ratio swimmers.
$Pe{-}\unicode[STIX]{x1D705}$ plane, thereby highlighting the singular behaviour of infinite-aspect-ratio swimmers.