Hostname: page-component-5f745c7db-6bmsf Total loading time: 0 Render date: 2025-01-06T08:31:14.183Z Has data issue: true hasContentIssue false
  • English
  • Français

A point vortex transportation model for yawed wind turbine wakes

Published online by Cambridge University Press:  11 March 2020

Haohua Zong Open the ORCID record for Haohua Zong [Opens in a new window]  and
Fernando Porté-Agel Open the ORCID record for Fernando Porté-Agel [Opens in a new window]
Haohua Zong*
Affiliation:
Wind Engineering and Renewable Energy Laboratory (WIRE), École Polytechnique Fédérale de Lausanne (EPFL), EPFL-ENAC-IIE-WIRE, 1015Lausanne, Switzerland
Fernando Porté-Agel
Affiliation:
Wind Engineering and Renewable Energy Laboratory (WIRE), École Polytechnique Fédérale de Lausanne (EPFL), EPFL-ENAC-IIE-WIRE, 1015Lausanne, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

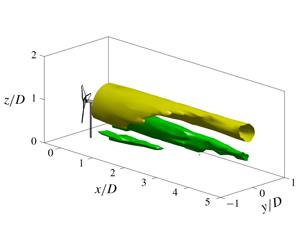
In this study, stereo particle imaging velocimetry measurements are performed at multiple streamwise locations behind a yawed wind turbine to reveal the formation mechanisms of the counter-rotating vortex pair (CVP), and a point vortex transportation (PVT) model is proposed to reproduce the top–down asymmetric kidney-shaped wake (also referred to as a curled wake). Results indicate that the CVP formed behind a yawed wind turbine originates from the complex interactions between the hub vortex and the streamwise components of the blade tip vortices, which is fundamentally different from the case of a yawed drag disk where the hub vortex is absent. Specifically, when the yaw angle exceeds a critical value, a small part of the streamwise vorticity shed from the rotor disk edge switches its sign from negative to positive and subsequently merges with the concentrated hub vortex under mutual induction, creating a patch of positive vorticity; meanwhile, the remaining streamwise vorticity distributed along the rotor edge curls and evolves into another patch of negative vorticity. These two patches of streamwise vorticity essentially constitute the CVP. Based on the physics learnt from the experiments, the non-uniform cross-stream velocity fields are first reconstructed by a cloud of point vortices distributed along the rotor edge and a hub vortex located in the rotor centre, and subsequently used to numerically solve a simplified transportation–diffusion equation of the wake velocity deficit, which altogether constitute the PVT model. This physics-based reduced-order model is the first model capable of accurately reproducing the wake deformation behind a yawed wind turbine.

JFM classification

Turbulent Flows: Turbulent boundary layers Wakes/Jets: Wakes Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 890 , 10 May 2020 , A8
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adaramola, M. S. & Krogstad, P.-Å 2011 Experimental investigation of wake effects on wind turbine performance. Renew. Energy 36 (8), 2078–2086.CrossRefGoogle Scholar
Anderson, J. D. 2010 Fundamentals of Aerodynamics. Tata McGraw-Hill Education.Google Scholar
Anderson, J. D., Degrez, G., Dick, E. & Grundmann, R. 2013 Computational Fluid Dynamics: An Introduction. Springer.Google Scholar
Barthelmie, R. J., Pryor, S. C., Frandsen, S. T., Hansen, K. S., Schepers, J. G., Rados, K., Schlez, W., Neubert, A., Jensen, L. E. & Neckelmann, S. 2010 Quantifying the impact of wind turbine wakes on power output at offshore wind farms. J. Atmos. Ocean. Technol. 27 (8), 1302–1317.CrossRefGoogle Scholar
Bastankhah, M. & Porté-Agel, F. 2014 A new analytical model for wind-turbine wakes. Renew. Energy 70, 116–123.CrossRefGoogle Scholar
Bastankhah, M. & Porté-Agel, F. 2016 Experimental and theoretical study of wind turbine wakes in yawed conditions. J Fluid Mech. 806, 506–541.CrossRefGoogle Scholar
Bastankhah, M. & Porté-Agel, F. 2017a A new miniature wind turbine for wind tunnel experiments. Part I: Design and performance. Energies 10 (7), 908.CrossRefGoogle Scholar
Bastankhah, M. & Porté-Agel, F. 2017b Wind tunnel study of the wind turbine interaction with a boundary-layer flow: upwind region, turbine performance, and wake region. Phys. Fluids 29 (6), 065105.CrossRefGoogle Scholar
Bastankhah, M. & Porté-Agel, F. 2019 Wind farm power optimization via yaw angle control: a wind tunnel study. J. Renew. Sustain. Energy 11 (2), 023301.CrossRefGoogle Scholar
Bay, C., King, J., Fleming, P., Mudafort, R. & Martinez, L.2019 Unlocking the full potential of wake steering: implementation and assessment of a controls-oriented model. Tech. Rep. NREL/JA-5000-73777. National Renewable Energy Lab (NREL).CrossRefGoogle Scholar
Branlard, E. & Gaunaa, M. 2015 Cylindrical vortex wake model: right cylinder. Wind Energy 18 (11), 1973–1987.CrossRefGoogle Scholar
Burton, T., Sharpe, D. & Jenkins, N. 2001 Handbook of Wind Energy. John Wiley & Sons.CrossRefGoogle Scholar
Damiani, R., Dana, S., Annoni, J., Fleming, P., Roadman, J., van Dam, J. & Dykes, K. 2018 Assessment of wind turbine component loads under yaw-offset conditions. Wind Energy Sci. 3 (1), 173–189.CrossRefGoogle Scholar
Dar, Z., Kar, K., Sahni, O. & Chow, J. H. 2016 Windfarm power optimization using yaw angle control. IEEE Trans. Sustain. Energy 8 (1), 104–116.CrossRefGoogle Scholar
Davey, A. 1962 The growth of Taylor vortices in flow between rotating cylinders. J. Fluid Mech. 14 (3), 336–368.CrossRefGoogle Scholar
Fleming, P., Annoni, J., Shah, J. J., Wang, L., Ananthan, S., Zhang, Z., Hutchings, K., Wang, P., Chen, W. & Chen, L. 2017 Field test of wake steering at an offshore wind farm. Wind Energy Sci. 2 (1), 229–239.CrossRefGoogle Scholar
Fleming, P., King, J., Dykes, K., Simley, E., Roadman, J., Scholbrock, A., Murphy, P., Lundquist, J. K., Moriarty, P., Fleming, K. et al. 2019 Initial results from a field campaign of wake steering applied at a commercial wind farm – Part 1. Wind Energy Sci. 4 (2), 273–285.CrossRefGoogle Scholar
Fleming, P. A., Gebraad, P. M. O., Lee, S., van Wingerden, J.-W., Johnson, K., Churchfield, M., Michalakes, J., Spalart, P. & Moriarty, P. 2014 Evaluating techniques for redirecting turbine wakes using sowfa. Renew. Energy 70, 211–218.CrossRefGoogle Scholar
Foti, D., Yang, X., Campagnolo, F., Maniaci, D. & Sotiropoulos, F. 2018 Wake meandering of a model wind turbine operating in two different regimes. Phys. Rev. Fluids 3 (5), 054607.CrossRefGoogle Scholar
Howland, M. F., Bossuyt, J., Martínez-Tossas, L. A., Meyers, J. & Meneveau, C. 2016 Wake structure in actuator disk models of wind turbines in yaw under uniform inflow conditions. J. Renew. Sustain. Energy 8 (4), 043301.CrossRefGoogle Scholar
Howland, M. F., Lele, S. K. & Dabiri, J. O. 2019 Wind farm power optimization through wake steering. Proc. Natl Acad. Sci. USA 116 (29), 14495–14500.CrossRefGoogle ScholarPubMed
Jensen, N. O.1983 A note on wind generator interaction. Tech. Rep. Ris-M-2411. Risoe National Laboratory.Google Scholar
Jiménez, Á., Crespo, A. & Migoya, E. 2010 Application of a LES technique to characterize the wake deflection of a wind turbine in yaw. Wind Energy 13 (6), 559–572.CrossRefGoogle Scholar
Kang, S., Yang, X. & Sotiropoulos, F. 2014 On the onset of wake meandering for an axial flow turbine in a turbulent open channel flow. J. Fluid Mech. 744, 376–403.CrossRefGoogle Scholar
Martínez-Tossas, L. A., Annoni, J., Fleming, P. A. & Churchfield, M. J. 2019 The aerodynamics of the curled wake: a simplified model in view of flow control. Wind Energy Sci. 4 (1), 127–138.CrossRefGoogle Scholar
Medici, D.2005 Experimental studies of wind turbine wakes: power optimisation and meandering. PhD thesis, KTH Royal Institute of Technology.Google Scholar
Medici, D. & Alfredsson, P. H. 2006 Measurements on a wind turbine wake: 3D effects and bluff body vortex shedding. Wind Energy 9 (3), 219–236.CrossRefGoogle Scholar
Niayifar, A. & Porté-Agel, F. 2016 Analytical modeling of wind farms: a new approach for power prediction. Energies 9 (9), 741.CrossRefGoogle Scholar
Park, J. & Law, K. H. 2015 Cooperative wind turbine control for maximizing wind farm power using sequential convex programming. Energy Convers. Manage. 101, 295–316.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Porté-Agel, F., Bastankhah, M. & Shamsoddin, S. 2020 Wind-turbine and wind-farm flows: a review. Boundary-Layer Meteorol. 174 (1), 1–59.CrossRefGoogle ScholarPubMed
Raffel, M., Willert, C. E., Scarano, F., Kähler, C. J., Wereley, S. T. & Kompenhans, J. 2018 Particle Image Velocimetry: A Practical Guide. Springer.CrossRefGoogle Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Sciacchitano, A. & Wieneke, B. 2016 PIV uncertainty propagation. Meas. Sci. Technol. 27 (8), 084006.CrossRefGoogle Scholar
Shapiro, C. R., Gayme, D. F. & Meneveau, C. 2018 Modelling yawed wind turbine wakes: a lifting line approach. J. Fluid Mech. 841, R1.CrossRefGoogle Scholar
Stevens, R. J. A. M. & Meneveau, C. 2017 Flow structure and turbulence in wind farms. Annu. Rev. Fluid Mech. 49, 311–339.CrossRefGoogle Scholar
Türk, M. & Emeis, S. 2010 The dependence of offshore turbulence intensity on wind speed. J. Wind Engng Ind. Aerodyn. 98 (8-9), 466–471.CrossRefGoogle Scholar
Vollmer, L., Steinfeld, G., Heinemann, D. & Kühn, M. 2016 Estimating the wake deflection downstream of a wind turbine in different atmospheric stabilities: an LES study. Wind Energy Sci. 1 (2), 129–141.CrossRefGoogle Scholar
Wu, J.-Z., Ma, H.-Y. & Zhou, M.-D. 2007 Vorticity and Vortex Dynamics. Springer.Google Scholar
Wu, Y.-T. & Porté-Agel, F. 2011 Large-eddy simulation of wind-turbine wakes: evaluation of turbine parametrisations. Boundary-Layer Meteorol. 138 (3), 345–366.CrossRefGoogle Scholar

Zong and Porté-Agel supplementary movie 1

Evolution of the cross-stream velocity and vorticity fields simulated by the PVT model at a yaw angle of 0 degrees

Download Zong and Porté-Agel supplementary movie 1(Video)
Video 4.4 MB

Zong and Porté-Agel supplementary movie 2

Evolution of the cross-stream velocity and vorticity fields simulated by the PVT model at a yaw angle of -10 degrees

Download Zong and Porté-Agel supplementary movie 2(Video)
Video 5 MB

Zong and Porté-Agel supplementary movie 3

Evolution of the cross-stream velocity and vorticity fields simulated by the PVT model at a yaw angle of -20 degrees

Download Zong and Porté-Agel supplementary movie 3(Video)
Video 5.3 MB

Zong and Porté-Agel supplementary movie 4

Evolution of the cross-stream velocity and vorticity fields simulated by the PVT model at a yaw angle of -30 degrees
Download Zong and Porté-Agel supplementary movie 4(Video)
Video 5.4 MB

Zong and Porté-Agel supplementary movie 5

Evolution of the cross-stream velocity and vorticity fields simulated by the PVT model at a yaw angle of 30 degrees

Download Zong and Porté-Agel supplementary movie 5(Video)
Video 5.4 MB