Hostname: page-component-5f745c7db-rgzdr Total loading time: 0 Render date: 2025-01-06T08:02:09.173Z Has data issue: true hasContentIssue false
  • English
  • Français

On the distinct drag, reconfiguration and wake of perforated structures

Published online by Cambridge University Press:  02 March 2020

Yaqing Jin ,
Jin-Tae Kim ,
Shyuan Cheng ,
Oumar Barry  and
Leonardo P. Chamorro Open the ORCID record for Leonardo P. Chamorro [Opens in a new window]
Yaqing Jin
Affiliation:
Department of Mechanical Engineering, The University of Texas at Dallas, Richardson, TX 75080, USA
Jin-Tae Kim
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA
Shyuan Cheng
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA
Oumar Barry
Affiliation:
Department of Mechanical Engineering, Virginia Tech, Blacksburg, VA 24061, USA
Leonardo P. Chamorro*
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA Civil and Environmental Engineering Department, University of Illinois, Urbana, IL 61801, USA Aerospace Engineering, University of Illinois, Urbana, IL 61801, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

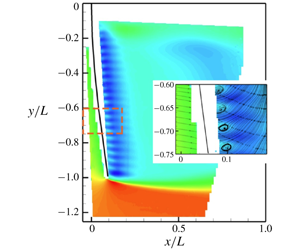
Using especially designed laboratory experiments, we demonstrate that the flow-driven deformation of sufficiently porous, wall-mounted, flexible plates can exhibit positive Vogel exponent $V$, i.e. drag proportional to the $(2+V)$ power of the incoming flow velocity. High-resolution force balance, planar particle image velocimetry and particle tracking velocimetry are used to measure the drag force, flow characteristics and plate bending. For a flexible plate with relatively high porosity given by an array of regularly spaced square openings, we derive a simple analytical argument that accounts for the sub-quadratic trends of the drag in a range of flow velocities spanning one order of magnitude. There, the drag experienced by the structure is modulated by the contributions of the local structure containing an open area. The effective approach velocity for each of these sections appears to increase monotonically with increased structure deformation due to the reduced effect of local wakes produced by adjacent areas. The uncovered aerodynamic behaviour may help to understand the complex flow–structure interaction of perforated structures in nature and engineering.

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 890 , 10 May 2020 , A1
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Alam, Md. M. & Zhou, Y. 2013 Intrinsic features of flow around two side-by-side square cylinders. Phys. Fluids 25 (8), 085106.CrossRefGoogle Scholar
Alben, S., Shelley, M. & Zhang, J. 2002 Drag reduction through self-similar bending of a flexible body. Nature 420 (6915), 479–481.CrossRefGoogle ScholarPubMed
Alben, S., Shelley, M. & Zhang, J. 2004 How flexibility induces streamlining in a two-dimensional flow. Phys. Fluids 16 (5), 1694–1713.CrossRefGoogle Scholar
Barry, O. R. & Tanbour, E. Y. 2018 Resonant frequencies of perforated plates with rectangular slots. P I Mech. Engng C-J Mec. 232 (7), 1247–1254.CrossRefGoogle Scholar
Betz, A. 1920 Das Maximum der theoretisch möglishen Ausnützung des Windes durch Windmotoren. Zeitschr. Gesam. Turbinenw. 26, 307–309.Google Scholar
Bhati, A., Sawanni, R., Kulkarni, K. & Bhardwaj, R. 2018 Role of skin friction drag during flow-induced reconfiguration of a flexible thin plate. J. Fluid Struct. 77, 134–150.CrossRefGoogle Scholar
Castro, I. P. 1971 Wake characteristics of two-dimensional perforated plates normal to an air-stream. J. Fluid Mech. 46 (3), 599–609.CrossRefGoogle Scholar
Crawford, C. & Platts, J. 2008 Updating and optimization of a coning rotor concept. J. Solar Energy Engng 130 (3), 031002.Google Scholar
Cummins, C., Seale, M., Macente, A., Certini, D., Mastropaolo, E., Viola, I. M. & Nakayama, N. 2018 A separated vortex ring underlies the flight of the dandelion. Nature 562 (7727), 414.CrossRefGoogle ScholarPubMed
Daniel, T. L. & Combes, S. A. 2002 Flexible wings and fins: bending by inertial or fluid-dynamic forces? Integr. Compar. Biol. 42 (5), 1044–1049.CrossRefGoogle ScholarPubMed
Gosselin, F., De Langre, E. & Machado-Almeida, B. A. 2010 Drag reduction of flexible plates by reconfiguration. J. Fluid Mech. 650, 319–341.CrossRefGoogle Scholar
Gosselin, F. P. & De Langre, E. 2011 Drag reduction by reconfiguration of a poroelastic system. J. Fluid Struct. 27 (7), 1111–1123.CrossRefGoogle Scholar
Graham, J. M. R. 1976 Turbulent flow past a porous plate. J. Fluid Mech. 73 (3), 565–591.CrossRefGoogle Scholar
Guttag, M., Karimi, H. H., Falcón, C. & Reis, P. M. 2018 Aeroelastic deformation of a perforated strip. Phys. Rev. Fluids 3 (1), 014003.CrossRefGoogle Scholar
Harder, D. L., Speck, O., Hurd, C. L. & Speck, T. 2004 Reconfiguration as a prerequisite for survival in highly unstable flow-dominated habitats. J. Plant Growth Regul. 23 (2), 98–107.CrossRefGoogle Scholar
Hemmati, A., Wood, D. H. & Martinuzzi, R. J. 2016 Characteristics of distinct flow regimes in the wake of an infinite span normal thin flat plate. Intl J. Heat Fluid Flow 62, 423–436.CrossRefGoogle Scholar
Jin, Y. & Chamorro, L. P. 2017 Passive pitching of splitters in the trailing edge of elliptic cylinders. J. Fluid Mech. 826, 363–375.CrossRefGoogle Scholar
Jin, Y., Kim, J.-T. & Chamorro, L. P. 2018a Instability-driven frequency decoupling between structure dynamics and wake fluctuations. Phys. Rev. Fluids 3, 044701.CrossRefGoogle Scholar
Jin, Y., Kim, J.-T., Fu, S. & Chamorro, L. P. 2019 Flow-induced motions of flexible plates: fluttering, twisting and orbital modes. J. Fluid Mech. 864, 273–285.CrossRefGoogle Scholar
Jin, Y., Yan, L., Qiu, H. & Chamorro, L. P. 2018b Turbulence-driven reverse lift on two-dimensional and three-dimensional structures. Phys. Rev. E 98 (3), 033106.Google Scholar
Kim, D., Cossé, J., Cerdeira, C. H. & Gharib, M. 2013 Flapping dynamics of an inverted flag. J. Fluid Mech. 736, R1.CrossRefGoogle Scholar
Kim, J.-T., Kim, D., Liberzon, A. & Chamorro, L. P. 2016 Three-dimensional particle tracking velocimetry for turbulence applications: case of a jet flow. J. Vis. Exp. 108, e53745.Google Scholar
Koo, J.-K. & James, D. F. 1973 Fluid flow around and through a screen. J. Fluid Mech. 60 (3), 513–538.CrossRefGoogle Scholar
Laws, E. M. & Livesey, J. L. 1978 Flow through screens. Annu. Rev. Fluid Mech. 10 (1), 247–266.CrossRefGoogle Scholar
Leclercq, T. & De Langre, E. 2016 Drag reduction by elastic reconfiguration of non-uniform beams in non-uniform flows. J. Fluid Struct. 60, 114–129.CrossRefGoogle Scholar
Lee, J.-K. & Kim, J.-G. 2005 An analytical study on prediction of effective elastic constants of perforated plate. J. Mech. Sci. Technol. 19 (12), 2224–2230.CrossRefGoogle Scholar
Liu, B., Hamed, A. M., Jin, Y. & Chamorro, L. P. 2017 Influence of vortical structure impingement on the oscillation and rotation of flat plates. J. Fluid Struct. 70, 417–427.CrossRefGoogle Scholar
Ljungkrona, L., Norberg, C. H. & Sunden, B. 1991 Free-stream turbulence and tube spacing effects on surface pressure fluctuations for two tubes in an in-line arrangement. J. Fluid Struct. 5 (6), 701–727.CrossRefGoogle Scholar
Luhar, M. & Nepf, H. M. 2011 Flow-induced reconfiguration of buoyant and flexible aquatic vegetation. Limnol. Oceanogr. 56 (6), 2003–2017.CrossRefGoogle Scholar
Luschi, L. & Pieri, F. 2014 An analytical model for the determination of resonance frequencies of perforated beams. J. Micromech. Microengng 24 (5), 055004.Google Scholar
Ma, S., Kang, C.-W., Lim, T.-B. A., Wu, C.-H. & Tutty, O. 2017 Wake of two side-by-side square cylinders at low Reynolds numbers. Phys. Fluids 29 (3), 033604.CrossRefGoogle Scholar
Niu, J. & Zhu, Z. 2006 Numerical study of three-dimensional flows around two identical square cylinders in staggered arrangements. Phys. Fluids 18 (4), 044106.CrossRefGoogle Scholar
Santhanakrishnan, A., Robinson, A. K., Jones, S., Low, A. A., Gadi, S., Hedrick, T. L. & Miller, L. A. 2014 Clap and fling mechanism with interacting porous wings in tiny insect flight. J. Expl Biol. 217 (21), 3898–3909.CrossRefGoogle ScholarPubMed
Stanford, B., Ifju, P., Albertani, R. & Shyy, W. 2008 Fixed membrane wings for micro air vehicles: experimental characterization, numerical modeling, and tailoring. Prog. Aerosp. Sci. 44 (4), 258–294.CrossRefGoogle Scholar
Steiros, K. & Hultmark, M. 2018 Drag on flat plates of arbitrary porosity. J. Fluid Mech. 853, R3.CrossRefGoogle Scholar
Sumner, D., Richards, M. D. & Akosile, O. O. 2005 Two staggered circular cylinders of equal diameter in cross-flow. J. Fluid Struct. 20 (2), 255–276.CrossRefGoogle Scholar
Sumner, D., Wong, S. S. T., Price, S. J. & Paidoussis, M. P. 1999 Fluid behaviour of side-by-side circular cylinders in steady cross-flow. J. Fluid Struct. 13 (3), 309–338.CrossRefGoogle Scholar
Taylor, G. I. 1952 Analysis of the swimming of long and narrow animals. Proc. R. Soc. Lond. A 214 (1117), 158–183.Google Scholar
Tunnicliffe, V. 1982 The effects of wave-induced flow on a reef coral. J. Exp. Mar. Biol. Ecol. 64 (1), 1–10.CrossRefGoogle Scholar
Vogel, S. 1984 Drag and flexibility in sessile organisms. Am. Zool. 24 (1), 37–44.CrossRefGoogle Scholar
Vogel, S. 1989 Drag and reconfiguration of broad leaves in high winds. J. Expl Bot. 40 (8), 941–948.CrossRefGoogle Scholar
Vogel, S. 2009 Leaves in the lowest and highest winds: temperature, force and shape. New Phytol. 183 (1), 13–26.CrossRefGoogle ScholarPubMed
Vollsinger, S., Mitchell, S. J., Byrne, K. E., Novak, M. D. & Rudnicki, M. 2005 Wind tunnel measurements of crown streamlining and drag relationships for several hardwood species. Can. J. Forest Res. 35 (5), 1238–1249.CrossRefGoogle Scholar
Younis, M. Y., Alam, M. M. & Zhou, Y. 2016 Flow around two non-parallel tandem cylinders. Phys. Fluids 28 (12), 125106.CrossRefGoogle Scholar
Zhu, L. 2008 Scaling laws for drag of a compliant body in an incompressible viscous flow. J. Fluid Mech. 607, 387–400.CrossRefGoogle Scholar
Zhu, L. & Peskin, C. S. 2007 Drag of a flexible fiber in a 2D moving viscous fluid. Comput. Fluids 36 (2), 398–406.CrossRefGoogle Scholar