Hostname: page-component-5f745c7db-sbzbt Total loading time: 0 Render date: 2025-01-06T08:23:15.188Z Has data issue: true hasContentIssue false
  • English
  • Français

Shear-induced migration of microswimmers in pressure-driven channel flow

Published online by Cambridge University Press:  12 March 2020

Laxminarsimharao Vennamneni Open the ORCID record for Laxminarsimharao Vennamneni [Opens in a new window] ,
Sankalp Nambiar  and
Ganesh Subramanian Open the ORCID record for Ganesh Subramanian [Opens in a new window]
Laxminarsimharao Vennamneni
Affiliation:
Engineering Mechanics Unit, JNCASR, Jakkur, Bangalore560064, India
Sankalp Nambiar
Affiliation:
Engineering Mechanics Unit, JNCASR, Jakkur, Bangalore560064, India
Ganesh Subramanian*
Affiliation:
Engineering Mechanics Unit, JNCASR, Jakkur, Bangalore560064, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

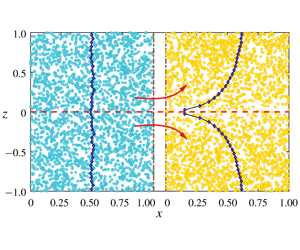
We study shear-induced migration in a dilute suspension of microswimmers (modelled as active Brownian particles or ABPs) subject to plane Poiseuille flow. For wide channels characterized by $U_{s}/HD_{r}\ll 1$, the separation between time scales characterizing the swimmer orientation dynamics (of $O(D_{r}^{-1})$) and those that characterize migration across the channel (of $O(H^{2}D_{r}/U_{s}^{2})$), allows for use of the method of multiple scales to derive a drift-diffusion equation for the swimmer concentration profile; here, $U_{s}$ is the swimming speed, $H$ is the channel half-width and $D_{r}$ is the swimmer rotary diffusivity. The steady state concentration profile is a function of the Péclet number, $Pe=U_{f}/(D_{r}H)$ ($U_{f}$ being the channel centreline velocity), and the swimmer aspect ratio $\unicode[STIX]{x1D705}$. Swimmers with $\unicode[STIX]{x1D705}\gg 1$ (with $\unicode[STIX]{x1D705}\sim O(1)$), in the regime $1\ll \text{Pe}\ll \unicode[STIX]{x1D705}^{3}$ ($Pe\sim O(1)$), migrate towards the channel walls, corresponding to a high-shear trapping behaviour. For $Pe\gg \unicode[STIX]{x1D705}^{3}$ ($Pe\gg 1$ for $\unicode[STIX]{x1D705}\sim O(1)$), however, swimmers migrate towards the centreline, corresponding to a low-shear trapping behaviour. Interestingly, within the low-shear trapping regime, swimmers with $\unicode[STIX]{x1D705}<2$ asymptote to a $Pe$-independent concentration profile for large $Pe$, while those with $\unicode[STIX]{x1D705}\geqslant 2$ exhibit a ‘centreline collapse’ for $Pe\rightarrow \infty$. The prediction of low-shear trapping, validated by Langevin simulations, is the first explanation of recent experimental observations (Barry et al., J. R. Soc. Interface, vol. 12 (112), 2015, 20150791). We organize the high-shear and low-shear trapping regimes on a $Pe{-}\unicode[STIX]{x1D705}$ plane, thereby highlighting the singular behaviour of infinite-aspect-ratio swimmers.

JFM classification

Biological Fluid Dynamics: Micro-organism dynamics Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 890 , 10 May 2020 , A15
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables, vol. 55. Courier Corporation.Google Scholar
Arfken, G. B. & Weber, H. J. 1999 Mathematical Methods for Physicists. American Association of Physics Teachers.Google Scholar
Barry, M. T., Rusconi, R., Guasto, J. S. & Stocker, R. 2015 Shear-induced orientational dynamics and spatial heterogeneity in suspensions of motile phytoplankton. J. R. Soc. Interface 12 (112), 20150791.CrossRefGoogle ScholarPubMed
Bearon, R. N. & Hazel, A. L. 2015 The trapping in high-shear regions of slender bacteria undergoing chemotaxis in a channel. J. Fluid Mech. 771, R3.CrossRefGoogle Scholar
Bechtel, T. M. & Khair, A. S. 2017 Linear viscoelasticity of a dilute active suspension. Rheol. Acta 56 (2), 149–160.CrossRefGoogle Scholar
Berg, H. C. 1993 Random Walks in Biology. Princeton University Press.Google Scholar
Berg, H. C. 2008 E. Coli in Motion. Springer.Google Scholar
Berke, A. P., Turner, L., Berg, H. C. & Lauga, E. 2008 Hydrodynamic attraction of swimming microorganisms by surfaces. Phys. Rev. Lett. 101 (3), 038102.CrossRefGoogle ScholarPubMed
Brennen, C. & Winet, H. 1977 Fluid mechanics of propulsion by cilia and flagella. Annu. Rev. Fluid Mech. 9 (1), 339–398.CrossRefGoogle Scholar
Brenner, H. 1974 Rheology of a dilute suspension of axisymmetric Brownian particles. Intl J. Multiphase Flow 1 (2), 195–341.CrossRefGoogle Scholar
Chaturvedi, N., Hong, Y., Sen, A. & Velegol, D. 2010 Magnetic enhancement of phototaxing catalytic motors. Langmuir 26 (9), 6308–6313.CrossRefGoogle ScholarPubMed
Chilukuri, S., Collins, C. H. & Underhill, P. T. 2014 Impact of external flow on the dynamics of swimming microorganisms near surfaces. J. Phys.: Condens. Matter 26 (11), 115101.Google ScholarPubMed
Chilukuri, S., Collins, C. H. & Underhill, P. T. 2015 Dispersion of flagellated swimming microorganisms in planar Poiseuille flow. Phys. Fluids 27 (3), 031902.CrossRefGoogle Scholar
Costanzo, A., Elgeti, J., Auth, T., Gompper, G. & Ripoll, M. 2014 Motility-sorting of self-propelled particles in microchannels. Europhys. Lett. 107 (3), 36003.CrossRefGoogle Scholar
Darnton, N. C., Turner, L., Rojevsky, S. & Berg, H. C. 2007 On torque and tumbling in swimming Escherichia coli. J. Bacteriol. 189 (5), 1756–1764.CrossRefGoogle ScholarPubMed
Das, D. & Lauga, E. 2018 Computing the motor torque of Escherichia Coli. Soft Matt. 14 (29), 5955–5967.CrossRefGoogle ScholarPubMed
Das, S., Gompper, G. & Winkler, R. G. 2018 Confined active Brownian particles: theoretical description of propulsion-induced accumulation. New J. Phys. 20 (1), 015001.Google Scholar
Doi, M. & Edwards, S. F. 1978 Dynamics of rod-like macromolecules in concentrated solution. Part 2. J. Chem. Soc. Faraday Trans. 74, 918–932.CrossRefGoogle Scholar
Dombrowski, C., Cisneros, L., Chatkaew, S., Goldstein, R. E. & Kessler, J. O. 2004 Self-concentration and large-scale coherence in bacterial dynamics. Phys. Rev. Lett. 93 (9), 098103.CrossRefGoogle ScholarPubMed
Ebbens, S., Gregory, D. A., Dunderdale, G., Howse, J. R., Ibrahim, Y., Liverpool, T. B. & Golestanian, R. 2014 Electrokinetic effects in catalytic platinum-insulator janus swimmers. Europhys. Lett. 106 (5), 58003.CrossRefGoogle Scholar
Elgeti, J. & Gompper, G. 2009 Self-propelled rods near surfaces. Europhys. Lett. 85 (3), 38002.CrossRefGoogle Scholar
Elgeti, J. & Gompper, G. 2013 Wall accumulation of self-propelled spheres. Europhys. Lett. 101 (4), 48003.CrossRefGoogle Scholar
Elgeti, J. & Gompper, G. 2016 Microswimmers near surfaces. Eur. Phys. J. 225 (11–12), 2333–2352.Google Scholar
Elgeti, J., Winkler, R. G. & Gompper, G. 2015 Physics of microswimmers single particle motion and collective behavior: a review. Rep. Prog. Phys. 78 (5), 056601.Google ScholarPubMed
Ezhilan, B., Alonso-Matilla, R. & Saintillan, D. 2015 On the distribution and swim pressure of run-and-tumble particles in confinement. J. Fluid Mech. 781, R4.CrossRefGoogle Scholar
Ezhilan, B. & Saintillan, D. 2015 Transport of a dilute active suspension in pressure-driven channel flow. J. Fluid Mech. 777, 482–522.CrossRefGoogle Scholar
Fischer, P. & Ghosh, A. 2011 Magnetically actuated propulsion at low Reynolds numbers: towards nanoscale control. Nanoscale 3 (2), 557–563.CrossRefGoogle ScholarPubMed
Gadala-Maria, F. & Acrivos, A. 1980 Shear-induced structure in a concentrated suspension of solid spheres. J. Rheol. 24 (6), 799–814.CrossRefGoogle Scholar
Ghosh, A., Samuel, J. & Sinha, S. 2012 A gaussian for diffusion on the sphere. Europhys. Lett. 98 (3), 30003.CrossRefGoogle Scholar
Gray, J. & Hancock, G. J. 1955 The propulsion of sea-urchin spermatozoa. J. Expl Biol. 32 (4), 802–814.Google Scholar
Guasto, J. S., Rusconi, R. & Stocker, R. 2012 Fluid mechanics of planktonic microorganisms. Annu. Rev. Fluid Mech. 44, 373–400.CrossRefGoogle Scholar
Guo, S., Samanta, D., Peng, Y., Xu, X. & Cheng, X. 2018 Symmetric shear banding and swarming vortices in bacterial superfluids. Proc. Natl Acad. Sci. USA 115 (28), 7212–7217.CrossRefGoogle ScholarPubMed
Hancock, G. J. 1953 The self-propulsion of microscopic organisms through liquids. Proc. R. Soc. Lond. A 217 (1128), 96–121.Google Scholar
Hinch, E. J. & Leal, L. G. 1972a The effect of Brownian motion on the rheological properties of a suspension of non-spherical particles. J. Fluid Mech. 52 (4), 683–712.CrossRefGoogle Scholar
Hinch, E. J. & Leal, L. G. 1972b Note on the rheology of a dilute suspension of dipolar spheres with weak Brownian couples. J. Fluid Mech. 56 (4), 803–813.CrossRefGoogle Scholar
Hinch, E. J. & Leal, L. G. 1973 Time-dependent shear flows of a suspension of particles with weak Brownian rotations. J. Fluid Mech. 57 (4), 753–767.CrossRefGoogle Scholar
Kasyap, T. V. & Koch, D. L. 2012 Chemotaxis driven instability of a confined bacterial suspension. Phys. Rev. Lett. 108 (3), 038101.CrossRefGoogle ScholarPubMed
Kasyap, T. V. & Koch, D. L. 2014 Instability of an inhomogeneous bacterial suspension subjected to a chemo-attractant gradient. J. Fluid Mech. 741, 619–657.CrossRefGoogle Scholar
Kim, M. K., Drescher, K., Pak, O. S., Bassler, B. L. & Stone, H. A. 2014 Filaments in curved streamlines: rapid formation of Staphylococcus aureus biofilm streamers. New J. Phys. 16 (6), 065024.Google ScholarPubMed
Kim, S. & Karrila, S. J. 2005 Microhydrodynamics: Principles and Selected Applications. Dover Publications.Google Scholar
Koch, D. L. & Subramanian, G. 2011 Collective hydrodynamics of swimming microorganisms: living fluids. Annu. Rev. Fluid Mech. 43, 637–659.CrossRefGoogle Scholar
Koh, C. J., Hookham, P. & Leal, L. G. 1994 An experimental investigation of concentrated suspension flows in a rectangular channel. J. Fluid Mech. 266, 1–32.CrossRefGoogle Scholar
Krishnamurthy, D. & Subramanian, G. 2015 Collective motion in a suspension of micro-swimmers that run-and-tumble and rotary diffuse. J. Fluid Mech. 781, 422–466.CrossRefGoogle Scholar
Lauga, E. & Powers, T. R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72 (9), 096601.Google Scholar
Leal, L. G. & Hinch, E. J. 1971 The effect of weak Brownian rotations on particles in shear flow. J. Fluid Mech. 46 (4), 685–703.CrossRefGoogle Scholar
Leal, L. G. & Hinch, E. J. 1972 The rheology of a suspension of nearly spherical particles subject to Brownian rotations. J. Fluid Mech. 55 (4), 745–765.CrossRefGoogle Scholar
Leal, L. G. & Hinch, E. J. 1973 Theoretical studies of a suspension of rigid particles affected by Brownian couples. Rheol. Acta 12 (2), 127–132.CrossRefGoogle Scholar
Leighton, D. & Acrivos, A. 1987 The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439.CrossRefGoogle Scholar
Leptos, K. C., Guasto, J. S., Gollub, J. P., Pesci, A. I. & Goldstein, R. E. 2009 Dynamics of enhanced tracer diffusion in suspensions of swimming eukaryotic microorganisms. Phys. Rev. Lett. 103 (19), 198103.CrossRefGoogle ScholarPubMed
López, H. M., Gachelin, J., Douarche, C., Auradou, H. & Clément, E. 2015 Turning bacteria suspensions into superfluids. Phys. Rev. Lett. 115 (2), 028301.CrossRefGoogle ScholarPubMed
Marchetti, M. C., Joanny, J.-F., Ramaswamy, S., Liverpool, T. B., Prost, J., Rao, M. & Simha, R. A. 2013 Hydrodynamics of soft active matter. Rev. Mod. Phys. 85 (3), 1143.CrossRefGoogle Scholar
Marcos, Fu, H. C., Powers, T. R. & Stocker, R. 2012 Bacterial rheotaxis. Proc. Natl Acad. Sci. USA 109, 4780–4785.CrossRefGoogle Scholar
Marcos & Stocker, R. 2006 Microorganisms in vortices: a microfluidic setup. Limnol. Oceanogr. 4 (10), 392–398.CrossRefGoogle Scholar
Messiah, A. 1962 Quantum Mechanics, vol. 2, appendix C. North-Holland.Google Scholar
Moran, J. L. & Posner, J. D. 2017 Phoretic self-propulsion. Annu. Rev. Fluid Mech. 49, 511–540.CrossRefGoogle Scholar
Nambiar, S., Garg, P. & Subramanian, G.2019a Enhanced velocity fluctuations in interacting swimmer suspensions. arXiv:1902.05304.Google Scholar
Nambiar, S., Nott, P. R. & Subramanian, G. 2017 Stress relaxation in a dilute bacterial suspension. J. Fluid Mech. 812, 41–64.CrossRefGoogle Scholar
Nambiar, S., Phanikanth, S., Nott, P. R. & Subramanian, G. 2019b Stress relaxation in a dilute bacterial suspension: The active-passive transition. J. Fluid Mech. 870, 1072–1104.CrossRefGoogle Scholar
Nitsche, L. C. & Hinch, E. J. 1997 Shear-induced lateral migration of Brownian rigid rods in parabolic channel flow. J. Fluid Mech. 332, 1–21.CrossRefGoogle Scholar
Nott, P. R. & Brady, J. F. 1994 Pressure-driven flow of suspensions: simulation and theory. J. Fluid Mech. 275, 157–199.CrossRefGoogle Scholar
Patteson, A. E., Gopinath, A., Purohit, P. K. & Arratia, P. E. 2016 Particle diffusion in active fluids is non-monotonic in size. Soft Matt. 12 (8), 2365–2372.CrossRefGoogle ScholarPubMed
Pedley, T. J. & Kessler, J. O. 1992 Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 24 (1), 313–358.CrossRefGoogle Scholar
Peyer, K. E., Zhang, L. & Nelson, B. J. 2013 Bio-inspired magnetic swimming microrobots for biomedical applications. Nanoscale 5 (4), 1259–1272.CrossRefGoogle ScholarPubMed
Rusconi, R., Garren, M. & Stocker, R. 2014a Microfluidics expanding the frontiers of microbial ecology. Annu. Rev. Biophys. 43, 65–91.CrossRefGoogle Scholar
Rusconi, R., Guasto, J. S. & Stocker, R. 2014b Bacterial transport suppressed by fluid shear. Nat. Phys. 10 (3), 212.CrossRefGoogle Scholar
Rusconi, R., Lecuyer, S., Guglielmini, L. & Stone, H. A. 2010 Laminar flow around corners triggers the formation of biofilm streamers. J. R. Soc. Interface 7 (50), 1293–1299.CrossRefGoogle ScholarPubMed
Saintillan, D. 2010a The dilute rheology of swimming suspensions: A simple kinetic model. Expt. Mech. 50, 1275–1281.CrossRefGoogle Scholar
Saintillan, D. 2010b Extensional rheology of active suspensions. Phys. Rev. E 81 (5), 056307.Google Scholar
Saintillan, D. & Shelley, M. J. 2007 Orientational order and instabilities in suspensions of self-locomoting rods. Phys. Rev. Lett. 99 (5), 058102.CrossRefGoogle ScholarPubMed
Saintillan, D. & Shelley, M. J. 2008 Instabilities and pattern formation in active particle suspensions: kinetic theory and continuum simulations. Phys. Rev. Lett. 100 (17), 178103.CrossRefGoogle ScholarPubMed
Sokolov, A. & Aranson, I. S. 2016 Rapid expulsion of microswimmers by a vortical flow. Nat. Commun. 7, 11114.Google ScholarPubMed
Sokolov, A., Rubio, L. D., Brady, J. F. & Aranson, I. S. 2018 Instability of expanding bacterial droplets. Nat. Commun. 9 (1), 1322.CrossRefGoogle ScholarPubMed
Stenhammar, J., Nardini, C., Nash, R. W., Marenduzzo, D. & Morozov, A. 2017 Role of correlations in the collective behavior of microswimmer suspensions. Phys. Rev. Lett. 119 (2), 028005.CrossRefGoogle ScholarPubMed
Strednak, S., Shaikh, S., Butler, J. E. & Guazzelli, É. 2018 Shear-induced migration and orientation of rigid fibers in an oscillatory pipe flow. Phys. Rev. Fluids 3 (9), 091301.CrossRefGoogle Scholar
Subramanian, G. & Brady, J. F. 2004 Multiple scales analysis of the Fokker–Planck equation for simple shear flow. Physica A 334 (3–4), 343–384.CrossRefGoogle Scholar
Subramanian, G. & Koch, D. L. 2009 Critical bacterial concentration for the onset of collective swimming. J. Fluid Mech. 632, 359–400.CrossRefGoogle Scholar
Subramanian, G., Koch, D. L. & Fitzgibbon, S. R. 2011 The stability of a homogeneous suspension of chemotactic bacteria. Phys. Fluids 23 (4), 041901.CrossRefGoogle Scholar
Subramanian, G. & Nott, P. R. 2012 The fluid dynamics of swimming microorganisms and cells. J. Ind. Inst. Sci. 91 (3), 283–314.Google Scholar
Tailleur, J. & Cates, M. E. 2009 Sedimentation, trapping, and rectification of dilute bacteria. Europhys. Lett. 86 (6), 60002.CrossRefGoogle Scholar
Takatori, S. C. & Brady, J. F. 2017 Superfluid behavior of active suspensions from diffusive stretching. Phys. Rev. Lett. 118 (1), 018003.CrossRefGoogle ScholarPubMed
Takatori, S. C. & Brady, J. F. 2014 Swim stress, motion, and deformation of active matter: effect of an external field. Soft Matter 10 (47), 9433–9445.CrossRefGoogle ScholarPubMed
Takatori, S. C. & Brady, J. F. 2015 Towards a thermodynamics of active matter. Phys. Rev. E 91 (3), 032117.Google ScholarPubMed
Takatori, S. C., Yan, W. & Brady, J. F. 2014 Swim pressure: stress generation in active matter. Phys. Rev. Lett. 113 (2), 028103.CrossRefGoogle ScholarPubMed
Taylor, J. R. & Stocker, R. 2012 Trade-offs of chemotactic foraging in turbulent water. Science 338 (6107), 675–679.CrossRefGoogle ScholarPubMed
Underhill, P. T. & Graham, M. D. 2011 Correlations and fluctuations of stress and velocity in suspensions of swimming microorganisms. Phys. Fluids 23 (12), 121902.CrossRefGoogle Scholar
Underhill, P. T., Hernandez-Ortiz, J. P. & Graham, M. D. 2008 Diffusion and spatial correlations in suspensions of swimming particles. Phys. Rev. Lett. 100 (24), 248101.CrossRefGoogle ScholarPubMed
Vennamneni, L., Garg, P. & Subramanian, G. 2018 Concentration banding instability of a sheared bacterial suspension. J. Fluid Mech. (submitted) arXiv:1808.07805.Google Scholar
Wensink, H. H., Dunkel, J., Heidenreich, S., Drescher, K., Goldstein, R. E., Löwen, H. & Yeomans, J. M. 2012 Meso-scale turbulence in living fluids. Proc. Natl Acad. Sci. USA.CrossRefGoogle ScholarPubMed
Wu, X. L. & Libchaber, A. 2000 Particle diffusion in a quasi-two-dimensional bacterial bath. Phys. Rev. Lett. 84, 3017–3020.CrossRefGoogle Scholar
Zöttl, A. & Stark, H. 2013 Periodic and quasiperiodic motion of an elongated microswimmer in Poiseuille flow. Eur. Phys. J. E 36 (1), 4.Google ScholarPubMed