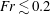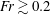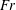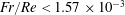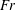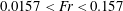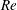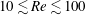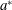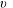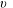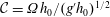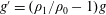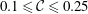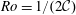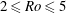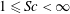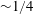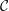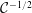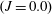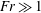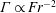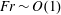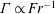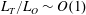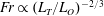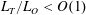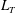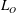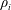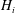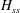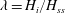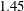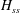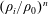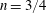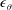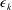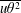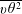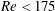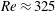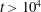JFM Perspectives
Beyond Kolmogorov cascades
-
- Published online by Cambridge University Press:
- 22 March 2019, P1
-
- Article
- Export citation
JFM Rapids
Pressure impulse theory for a slamming wave on a vertical circular cylinder
-
- Published online by Cambridge University Press:
- 20 March 2019, R1
-
- Article
- Export citation
A conditional space–time POD formalism for intermittent and rare events: example of acoustic bursts in turbulent jets
-
- Published online by Cambridge University Press:
- 02 April 2019, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Load and loss for high-speed lubrication flows of pressurized gases between non-concentric cylinders
-
- Published online by Cambridge University Press:
- 20 March 2019, pp. 1-25
-
- Article
- Export citation
Unstable jets generated by a sphere descending in a very strongly stratified fluid
-
- Published online by Cambridge University Press:
- 20 March 2019, pp. 26-44
-
- Article
- Export citation
Investigation of the influence of combustion-induced thermal expansion on two-point turbulence statistics using conditioned structure functions
-
- Published online by Cambridge University Press:
- 20 March 2019, pp. 45-76
-
- Article
- Export citation
Numerical analysis of flow-induced rotation of an S-shaped rotor
-
- Published online by Cambridge University Press:
- 21 March 2019, pp. 77-113
-
- Article
- Export citation
Rotating planar gravity currents at moderate Rossby numbers: fully resolved simulations and shallow-water modelling
-
- Published online by Cambridge University Press:
- 20 March 2019, pp. 114-145
-
- Article
- Export citation
A new model of shoaling and breaking waves. Part 2. Run-up and two-dimensional waves
-
- Published online by Cambridge University Press:
- 20 March 2019, pp. 146-194
-
- Article
- Export citation
Cascades of temperature and entropy fluctuations in compressible turbulence
-
- Published online by Cambridge University Press:
- 20 March 2019, pp. 195-215
-
- Article
- Export citation
Turbulence decay in a supersonic boundary layer subjected to a transverse sonic jet
-
- Published online by Cambridge University Press:
- 21 March 2019, pp. 216-249
-
- Article
- Export citation
Compressible unsteady Görtler vortices subject to free-stream vortical disturbances
-
- Published online by Cambridge University Press:
- 21 March 2019, pp. 250-299
-
- Article
- Export citation
The transient force profile of low-speed droplet impact: measurements and model
-
- Published online by Cambridge University Press:
- 21 March 2019, pp. 300-322
-
- Article
- Export citation
On the inference of the state of turbulence and mixing efficiency in stably stratified flows
-
- Published online by Cambridge University Press:
- 21 March 2019, pp. 323-333
-
- Article
- Export citation
Electrohydrodynamics of deflated vesicles: budding, rheology and pairwise interactions
-
- Published online by Cambridge University Press:
- 21 March 2019, pp. 334-347
-
- Article
- Export citation
Finite-amplitude steady-state wave groups with multiple near-resonances in finite water depth
-
- Published online by Cambridge University Press:
- 21 March 2019, pp. 348-373
-
- Article
- Export citation
Upward versus downward non-Boussinesq turbulent fountains
-
- Published online by Cambridge University Press:
- 21 March 2019, pp. 374-391
-
- Article
- Export citation
An empirical expression for
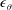 $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$ on the axis of a slightly heated turbulent round jet
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$ on the axis of a slightly heated turbulent round jet
-
- Published online by Cambridge University Press:
- 22 March 2019, pp. 392-413
-
- Article
- Export citation
Dynamics of spatially localized states in transitional plane Couette flow
-
- Published online by Cambridge University Press:
- 25 March 2019, pp. 414-437
-
- Article
- Export citation
On the time scales and structure of Lagrangian intermittency in homogeneous isotropic turbulence
-
- Published online by Cambridge University Press:
- 25 March 2019, pp. 438-481
-
- Article
- Export citation