Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-17T14:18:52.987Z Has data issue: false hasContentIssue false
  • English
  • Français

An empirical expression for 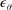$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$ on the axis of a slightly heated turbulent round jet

Published online by Cambridge University Press:  22 March 2019

J. Lemay Open the ORCID record for J. Lemay [Opens in a new window] ,
L. Djenidi Open the ORCID record for L. Djenidi [Opens in a new window] ,
R. A. Antonia  and
A. Benaïssa
J. Lemay*
Affiliation:
Department of Mechanical Engineering, Université Laval, 1065 avenue de la Médecine, Québec City, QC G1V 0A6, Canada
L. Djenidi
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
R. A. Antonia
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
A. Benaïssa
Affiliation:
Department of Mechanical and Aerospace Engineering, Royal Military College of Canada, PO Box 17000, Station Forces, Kingston, ON K7K 7B4, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Self-preservation analyses of the equations for the mean temperature and the second-order temperature structure function on the axis of a slightly heated turbulent round jet are exploited in an attempt to develop an analytical expression for 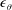$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$, the mean dissipation rate of 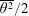$\overline{\unicode[STIX]{x1D703}^{2}}/2$, where 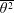$\overline{\unicode[STIX]{x1D703}^{2}}$ is the temperature variance. The analytical approach follows that of Thiesset et al. (J. Fluid Mech., vol. 748, 2014, R2) who developed an expression for 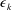$\unicode[STIX]{x1D716}_{k}$, the mean turbulent kinetic energy dissipation rate, using the transport equation for 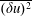$\overline{(\unicode[STIX]{x1D6FF}u)^{2}}$, the second-order velocity structure function. Experimental data show that complete self-preservation for all scales of motion is very well satisfied along the jet axis for streamwise distances larger than approximately 30 times the nozzle diameter. This validation of the analytical results is of particular interest as it provides justification and confidence in the analytical derivation of power laws representing the streamwise evolution of different physical quantities along the axis, such as: 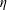$\unicode[STIX]{x1D702}$, 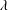$\unicode[STIX]{x1D706}$, 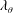$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$, 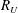$R_{U}$, 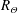$R_{\unicode[STIX]{x1D6E9}}$ (all representing characteristic length scales), the mean temperature excess 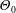$\unicode[STIX]{x1D6E9}_{0}$, the mixed velocity–temperature moments 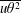$\overline{u\unicode[STIX]{x1D703}^{2}}$, 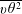$\overline{v\unicode[STIX]{x1D703}^{2}}$ and 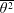$\overline{\unicode[STIX]{x1D703}^{2}}$ and 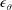$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$. Simple models are proposed for 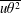$\overline{u\unicode[STIX]{x1D703}^{2}}$ and 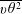$\overline{v\unicode[STIX]{x1D703}^{2}}$ in order to derive an analytical expression for 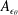$A_{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}}$, the prefactor of the power law describing the streamwise evolution of 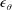$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}$. Further, expressions are also derived for the turbulent Péclet number and the thermal-to-mechanical time scale ratio. These expressions involve global parameters that are most likely to be influenced by the initial and/or boundary conditions and are therefore expected to be flow dependent.

JFM classification

Wakes/Jets: Jets Turbulent Flows: Turbulence modelling
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 392 - 413
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. & Mi, J. 1993 Temperature dissipation in a turbulent round jet. J. Fluid Mech. 250, 531–551.Google Scholar
Antonia, R. A., Ould-Rouis, M., Anselmet, F. & Zhu, Y. 1997 Analogy between predictions of Kolmogorov and Yaglom. J. Fluid Mech. 332, 395–409.Google Scholar
Antonia, R. A., Satyaprakash, R. J. & Hussain, A. K. M. F. 1980 Measurements of dissipation rate and some other characteristics of turbulent plane and circular jets. Phys. Fluids 23 (4), 695–700.Google Scholar
Antonia, R. A., Smalley, R. J., Zhou, T., Anselmet, F. & Danaila, L. 2004 Similarity solution of temperature structure functions in decaying homogeneous isotropic turbulence. Phys. Rev. E 69, 016305.Google Scholar
Antonia, R. A. & Van Atta, C. W. 1978 Structure functions of temperature fluctuations in turbulent shear flows. J. Fluid Mech. 84, 561–580.Google Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005a Scale-by-scale energy budget on the axis of a turbulent round jet. J. Turbul. 6, 1–11.Google Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005b Similarity in the far field of a turbulent round jet. Phys. Fluids 17, 1–14.Google Scholar
Chevray, R. & Tutu, N. K. 1978 Intermittency and preferential transport of heat in a round jet. J. Fluid Mech. 88 (01), 133–160.Google Scholar
Danaila, L., Anselmet, F., Zhou, T. & Antonia, R. A. 1999 A generalization of Yaglom’s equation which accounts for the large-scale forcing in heated decaying turbulence. J. Fluid Mech. 391, 359–372.Google Scholar
Danaila, L., Krawczynski, J. F., Thiesset, F. & Renou, B. 2012 Yaglom-like equation in axisymmetric anisotropic turbulence. Physica  D 241 (3), 216–223.Google Scholar
Darisse, A., Lemay, J & Benaïssa, A. 2013a Investigation of passive scalar mixing in a turbulent free jet using simultaneous LDV and cold wire measurements. Intl J. Heat Fluid Flow 44, 284–292.Google Scholar
Darisse, A., Lemay, J. & Benaïssa, A. 2013b LDV measurements of well converged third order moments in the far field of a free turbulent round jet. Exp. Therm. Fluid Sci. 44, 825–833.Google Scholar
Darisse, A., Lemay, J. & Benaïssa, A. 2014 Extensive study of temperature dissipation measurements on the centerline of a turbulent round jet based on the 𝜃2 /2 budget. Exp. Fluids 55 (1), 1–15.Google Scholar
Darisse, A., Lemay, J. & Benaïssa, A. 2015 Budgets of turbulent kinetic energy, Reynolds stresses, variance of temperature fluctuations and turbulent heat fluxes in a round jet. J. Fluid Mech. 774, 95–142.Google Scholar
Dekeyser, I. & Launder, B. E. 1983 A comparison of triple-moment temperature-velocity correlations in the asymmetric heated jet with alternative closure models. In Turbulent Shear Flows 4 (ed. Bradbury, L. J. S., Durst, F., Launder, B. E., Schmidt, F. W. & Whitelaw, J. H.), pp. 102–117. Springer.Google Scholar
Djenidi, L., Antonia, R. A., Lefeuvre, N. & Lemay, J. 2016 Complete self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 790, 57–70.Google Scholar
Ewing, D., Frohnapfel, B., George, W. K., Pedersen, J. M. & Westerweel, J. 2007 Two-point similarity in the round jet. J. Fluid Mech. 577, 309–330.Google Scholar
Friehe, C. A., Van Atta, C. W. & Gibson, C. H. 1971 Jet turbulence: dissipation rate measurements and correlations. Turbulent Shear Flows, AGARD CP-93, pp. 18.1–18.7.Google Scholar
Gibson, M. M. & Launder, B. E. 1976 On the calculation of horizontal, turbulent, free shear flows under gravitational influence. ASME J. Heat Transfer 98 (1), 81–87.Google Scholar
Hanjalić, K. & Launder, B. 2011 Modelling Turbulence in Engineering and the Environment: Second-Moments Routes to Closure. Cambridge University Press.Google Scholar
Hill, R. J. 1997 Applicability of Kolmogorov’s and Monin’s equations of turbulence. J. Fluid Mech. 353, 67–81.Google Scholar
Hill, R. J. 2001 Equations relating structure functions of all orders. J. Fluid Mech. 434, 379–388.Google Scholar
Hussein, H. J., Capp, S. P. & George, W. K. 1994 Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.Google Scholar
Lemay, J., Benaissa, A. & Antonia, R. A. 2003 Correction of cold-wire response for mean temperature dissipation rate measurements. Exp. Therm. Fluid Sci. 27 (2), 133–143; 6th International Thermal Anemometry Symposium.Google Scholar
Lemay, J. & Benaïssa, A. 2001 Improvement of cold-wire response for measurement of temperature dissipation. Exp. Fluids 31, 347–356.Google Scholar
Lemoine, F., Antoine, Y., Wolff, M. & Lebouche, M. 1999 Simultaneous temperature and 2D velocity measurements in a turbulent heated jet using combined laser-induces fluorescence and lda. Exp. Fluids 26, 315–323.Google Scholar
Mi, J., Xu, M. & Zhou, T. 2013 Reynolds number influence on statistical behaviors of turbulence in a circular free jet. Phys. Fluids 25, 075101.Google Scholar
Panchapakesan, N. R. & Lumley, J. L. 1993a Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 246, 197–223.Google Scholar
Panchapakesan, N. R. & Lumley, J. L. 1993b Turbulence measurements in axisymmetric jets of air and helium. Part 2. Helium jet. J. Fluid Mech. 246, 225–247.Google Scholar
Pietri, L., Amielh, M. & Anselmet, F. 2000 Simultaneous measurements of temperature and velocity fluctuations in a slightly heated jet combining a cold wire and Laser Doppler Anemometry. Intl J. Heat Fluid Flow 21 (1), 22–36.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Ruffin, E., Schiestel, R., Anselmet, F., Amielh, M. & Fulachier, L. 1994 Investigation of characteristic scales in variable density turbulent jets using a second-order model. Phys. Fluids 6 (8), 2785–2799.Google Scholar
Shivamoggi, B. K. & Antonia, R. A. 2000 Isotropic and axisymmetric turbulence of passive scalars. Fluid Dyn. Res. 26, 95–104.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Thiesset, F., Antonia, R. A. & Djenidi, L. 2014 Consequences of self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 748, R2.Google Scholar
Yaglom, A. M. 1949 On the local structure of the temperature field in a turbulent flow. Dokl. Akad. Nauk SSSR 69, 743–746.Google Scholar