Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-19T13:57:43.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite-amplitude steady-state wave groups with multiple near-resonances in finite water depth

Published online by Cambridge University Press:  21 March 2019

Z. Liu Open the ORCID record for Z. Liu [Opens in a new window]  and
D. Xie
Z. Liu*
Affiliation:
School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, PR China Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, PR China Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics (HUST), Wuhan 430074, PR China
D. Xie
Affiliation:
School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, PR China Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, PR China Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics (HUST), Wuhan 430074, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Finite-amplitude wave groups with multiple near-resonances are investigated to extend the existing results due to Liu et al. (J. Fluid Mech., vol. 835, 2018, pp. 624–653) from steady-state wave groups in deep water to steady-state wave groups in finite water depth. The slow convergence rate of the series solution in the homotopy analysis method and extra unpredictable high-frequency components in finite water depth make it hard to obtain finite-amplitude wave groups accurately. To overcome these difficulties, a solution procedure that combines the homotopy analysis method-based analytical approach and Galerkin method-based numerical approaches has been used. For weakly nonlinear wave groups, the continuum of steady-state resonance from deep water to finite water depth is established. As nonlinearity increases, the frequency bands broaden and more steady-state wave groups are obtained. Finite-amplitude wave groups with steepness no less than 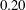$0.20$ are obtained and the resonant sets configuration of steady-state wave groups are analysed in different water depths. For waves in deep water, the majority of non-trivial components appear around the primary ones due to four-wave, six-wave, eight-wave or even ten-wave resonant interactions. The dominant role of four-wave resonant interactions for steady-state wave groups in deep water is demonstrated. For waves in finite water depth, additional non-trivial high-frequency components appear in the spectra due to three-wave, four-wave, five-wave or even six-wave resonant interactions with the components around the primary ones. The amplitude of these high-frequency components increases further as the water depth decreases. Resonances composed by components only around the primary ones are suppressed while resonances composed by components around the primary ones and from the high-frequency domain are enhanced. The spectrum of steady-state resonant wave groups changes with the water depth and the significant role of three-wave resonant interactions in finite water depth is demonstrated.

JFM classification

Waves/Free-surface Flows: Surface gravity waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 348 - 373
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. R., Liu, Y. M. & Yue, D. K. P. 2010 Oblique sub- and super-harmonic Bragg resonance of surface waves by bottom ripples. J. Fluid Mech. 643, 437–447.Google Scholar
Annenkov, S. Y. & Shrira, V. I. 2006 Role of non-resonant interactions in the evolution of nonlinear random water wave fields. J. Fluid Mech. 561, 181–208.Google Scholar
Benney, D. J. 1962 Non-linear gravity wave interactions. J. Fluid Mech. 14 (4), 577–584.Google Scholar
Davey, A. & Stewartson, F. R. S. K. 1974 On three-dimensional packets of surface waves. Proc. R. Soc. Lond. A 338, 101–110.Google Scholar
Dommermuth, D. G. & Yue, D. K. P. 1987 A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 184, 267–288.Google Scholar
Fenton, J. D. 1979 A high-order cnoidal wave theory. J. Fluid Mech. 94, 129–161.Google Scholar
Francius, M. & Kharif, C. 2006 Three-dimensional instabilities of periodic gravity waves in shallow water. J. Fluid Mech. 561, 417–437.Google Scholar
Freilich, M. H., Guza, R. T. & Elgar, S. L. 1990 Observations of nolinear effects in directional spectra of shoaling gravity waves. J. Geophys. Res. 95 (C6), 9645–9656.Google Scholar
Gramstad, O. 2014 The Zakharov equation with separate mean flow and mean surface. J. Fluid Mech. 740, 254–277.Google Scholar
Hammack, J. L. & Henderson, D. M. 1993 Resonant interactions among surface water waves. Annu. Rev. Fluid Mech. 25 (1), 55–97.Google Scholar
Hasselmann, K. 1962 On the non-linear energy transfer in a gravity-wave spectrum Part 1. General theory. J. Fluid Mech. 12 (4), 481–500.Google Scholar
Hasselmann, K. 1963a On the non-linear energy transfer in a gravity wave spectrum Part 2. Conservation theorems; wave–particle analogy; irrevesibility. J. Fluid Mech. 15 (2), 273–281.Google Scholar
Hasselmann, K. 1963b On the non-linear energy transfer in a gravity-wave spectrum. Part 3. Evaluation of the energy flux and swell–sea interaction for a Neumann spectrum. J. Fluid Mech. 15 (3), 385–398.Google Scholar
Hui, W. H. & Hamilton, J. 1979 Exact solutions of a three-dimensional nonlinear Schrodinger equation applied to gravity waves. J. Fluid Mech. 93 (1), 117–133.Google Scholar
Ioualalen, M. & Kharif, C. 1994 On the subharmonic instabilities of steady three-dimensional deep water waves. J. Fluid Mech. 262, 265–291.Google Scholar
Ioualalen, M., Okamura, M., Cornier, S., Kharif, C. & Roberts, A. J. 2006 Computation of short-crested deepwater waves. ASCE J. Waterway Port Coastal Ocean Engng 132 (3), 157–165.Google Scholar
Janssen, P. A. E. M. 2003 Nonlinear four-wave interactions and freak waves. J. Phys. Oceanogr. 33 (4), 863–884.Google Scholar
Janssen, P. A. E. M. & Onorato, M. 2007 The intermediate water depth limit of the Zakharov equation and consequences for wave prediction. J. Phys. Oceanogr. 37, 2389–2400.Google Scholar
Katsardi, V. & Swan, C. 2011 The evolution of large non-breaking waves in intermediate and shallow water. I. Numerical calculations of uni-directional seas. Proc. Math. Phys. Engng Sci. 467 (2127), 778–805.Google Scholar
Lavrova, O. T. 1983 On the lateral instability of waves on the surface of a finite-depth fluid. Izv. Atmos. Ocean. Phys. 19, 807–810.Google Scholar
Liao, S. J.1992 Proposed homotopy analysis techniques for the solution of nonlinear problems. PhD thesis, Shanghai Jiao Tong University.Google Scholar
Liao, S. J. 2003 Beyond Perturbation: Introduction to the Homotopy Analysis Method. CRC Press.Google Scholar
Liao, S. J. 2011 On the homotopy multiple-variable method and its applications in the interactions of nonlinear gravity waves. Commun. Nonlinear Sci. Numer. Simul. 16 (3), 1274–1303.Google Scholar
Liao, S. J. 2012 Homotopy Analysis Method in Nonlinear Differential Equations. Springer & Higher Education Press.Google Scholar
Liao, S. J., Xu, D. L. & Stiassnie, M. 2016 On the steady-state nearly resonant waves. J. Fluid Mech. 794, 175–199.Google Scholar
Liu, Z. & Liao, S. J. 2014 Steady-state resonance of multiple wave interactions in deep water. J. Fluid Mech. 742, 664–700.Google Scholar
Liu, Z., Xu, D. L., Li, J., Peng, T., Alsaedi, A. & Liao, S. J. 2015 On the existence of steady-state resonant waves in experiments. J. Fluid Mech. 763, 1–23.Google Scholar
Liu, Z., Xu, D. L. & Liao, S. J. 2017 Mass, momentum, and energy flux conservation between linear and nonlinear steady-state wave groups. Phys. Fluids 29 (12), 127104.Google Scholar
Liu, Z., Xu, D. L. & Liao, S. J. 2018 Finite amplitude steady-state wave groups with multiple near resonances in deep water. J. Fluid Mech. 835, 624–653.Google Scholar
Longuet-Higgins, M. S. & Smith, N. D. 1966 An experiment on third-order resonant wave interactions. J. Fluid Mech. 25 (03), 417–435.Google Scholar
Madsen, P. A. & Fuhrman, D. R. 2012 Third-order theory for multi-directional irregular waves. J. Fluid Mech. 698, 304–334.Google Scholar
McGoldrick, L. F., Phillips, O. M., Huang, N. E. & Hodgson, T. H. 1966 Measurements of third-order resonant wave interactions. J. Fluid Mech. 25 (03), 437–456.Google Scholar
Miao, S. & Liu, Y. M. 2015 Wave pattern in the wake of an arbitrary moving surface pressure disturbance. Phys. Fluids 27, 122102.Google Scholar
Okamura, M. 1996 Notes on short-crested waves in deep water. J. Phys. Soc. Japan 65 (9), 2841–2845.Google Scholar
Okamura, M. 2003 Standing gravity waves of large amplitude in deep water. Wave Motion 37 (2), 173–182.Google Scholar
Okamura, M. 2010 Almost limiting short-crested gravity waves in deep water. J. Fluid Mech. 646 (7), 481–503.Google Scholar
Onorato, M., Osborne, A. R., Janssen, P. A. E. M. & Resio, D. 2009 Four-wave resonant interactions in the classical quadratic Boussinesq equations. J. Fluid Mech. 618, 263–277.Google Scholar
Pan, Y. L. & Yue, D. K. P. 2014 Direct numerical investigation of turbulence of capillary waves. Phys. Rev. Lett. 113, 094501.Google Scholar
Pan, Y. L. & Yue, D. K. P. 2015 Decaying capillary wave turbulence under broad-scale dissipation. J. Fluid Mech. 780, R1.Google Scholar
Phillips, O. M. 1960 On the dynamics of unsteady gravity waves of finite amplitude Part 1. The elementary interactions. J. Fluid Mech. 9 (02), 193–217.Google Scholar
Phillips, O. M. 1981 Wave interactions – the evolution of an idea. J. Fluid Mech. 106 (1), 215–227.Google Scholar
Qi, Y. S., Wu, G. Y., Liu, Y. M., Kim, M. H. & Yue, D. K. P. 2018a Nonlinear phase-resolved reconstruction of irregular water waves. J. Fluid Mech. 838, 544–572.Google Scholar
Qi, Y. S., Wu, G. Y., Liu, Y. M. & Yue, D. K. P. 2018b Predictable zone for phase-resolved reconstruction and forecast of irregular waves. Wave Motion 77, 195–213.Google Scholar
Stiassnie, M. & Gramstad, O. 2009 On Zakharov’s kernel and the interaction of non-collinear wavetrains in finite water depth. J. Fluid Mech. 639, 433–442.Google Scholar
Stiassnie, M. & Shemer, L. 1984 On modifications of the Zakharov equation for surface gravity waves. J. Fluid Mech. 143, 47–67.Google Scholar
Stokes, G. G. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441–473.Google Scholar
Toffoli, A., Benoit, M., Onorato, M. & Bitner-Gregersen, E. M. 2009 The effect of third-order nonlinearity on statistical properties of random directional waves in finite depth. Nonlinear Process. Geophys. 16, 131–139.Google Scholar
Xu, D. L., Lin, Z. L., Liao, S. J. & Stiassnie, M. 2012 On the steady-state fully resonant progressive waves in water of finite depth. J. Fluid Mech. 710, 379–418.Google Scholar
Yang, X. Y., Dias, F. & Liao, S. J. 2018 On the steady-state resonant acoustic-gravity waves. J. Fluid Mech. 849, 111–135.Google Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9 (2), 190–194.Google Scholar
Zakharov, V. E. 1999 Statistical theory of gravity and capillary waves on the surface of a finite-depth fluid. Eur. J. Mech. (B/Fluids) 18 (3), 327–344.Google Scholar
Zakharov, V. E. & Kharitonov, V. G. 1970 Instability of monochromatic waves on the surface of a liquid of arbitrary depth. J. Appl. Mech. Tech. Phys. 11, 741–751.Google Scholar
Zhang, J. & Melville, W. K. 1987 Three-dimensional instabilities of nonlinear gravity-capillary waves. J. Fluid Mech. 174 (174), 187–208.Google Scholar
Zhong, X. X. & Liao, S. J. 2018a Analytic approximations of Von Kármán plate under arbitrary uniform pressure – equations in integral form. Sci. China – Phys. Mech. Astron. 61 (01), 014711.Google Scholar
Zhong, X. X. & Liao, S. J. 2018b On the limiting Stokes wave of extreme height in arbitrary water depth. J. Fluid Mech. 843, 653–679.Google Scholar