Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-19T14:08:00.831Z Has data issue: false hasContentIssue false
  • English
  • Français

The transient force profile of low-speed droplet impact: measurements and model

Published online by Cambridge University Press:  21 March 2019

Benjamin R. Mitchell Open the ORCID record for Benjamin R. Mitchell [Opens in a new window] ,
Joseph C. Klewicki Open the ORCID record for Joseph C. Klewicki [Opens in a new window] ,
Yannis P. Korkolis Open the ORCID record for Yannis P. Korkolis [Opens in a new window]  and
Brad L. Kinsey Open the ORCID record for Brad L. Kinsey [Opens in a new window]
Benjamin R. Mitchell*
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
Joseph C. Klewicki
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, 3010, Australia
Yannis P. Korkolis
Affiliation:
Department of Integrated Systems Engineering, The Ohio State University, Columbus, OH 45221, USA
Brad L. Kinsey
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The transient force exerted by a low-speed liquid droplet impinging onto a flat rigid surface is investigated experimentally. The measurements employ a high-sensitivity piezo-electric sensor, along with a high-speed camera, and cover four decades in droplet Reynolds number and greater than two decades in Weber number. Across these ranges, the peak of individual force profiles span from 3 mN to over 1300 mN. Once normalised, the force–time profiles support the existence of an inertially dominated self-similar regime. 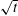Within this regime, previous numerical and theoretical studies predict a $\sqrt{t}$ dependence of impact normal force during the initial pre-peak rise. While our measurements confirm this finding, they also indicate that, after the peak force the profiles exhibit an exponential decay. This long-time decay law suggests treatment of the momentum transport from the droplet using a lumped model. An observed linear dependence between the force and force decay rate supports this approach. The reason for the efficacy of treating this system via a lumped model apparently connects to the physics right at the surface that limit the rate of momentum transport from the droplet to the surface. This is explored by estimating the momentum transfer by solely using the deforming droplet shape, but under the condition of negligible momentum gradients within the droplet. The short- and long-time solutions are combined and the resulting model equation is shown to accurately cover the entire force–time profile.

JFM classification

Drops and Bubbles: Drops
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 300 - 322
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmad, M., Schatz, M. & Casey, M. V. 2013 Experimental investigation of droplet size influence on low pressure steam turbine blade erosion. Wear 303 (1), 83–86.Google Scholar
Amirzadeh, B., Louhghalam, A., Raessi, M. & Tootkaboni, M. 2017 A computational framework for the analysis of rain-induced erosion in wind turbine blades. J. Wind Engng Ind. Aerodyn. 163, 33–43.Google Scholar
Association, Glycerine Producers’ 1963 Physical Properties of Glycerine and its Solutions. Glycerine Producers’ Association.Google Scholar
Baker, E. A. & Hunt, G. M. 1986 Erosion of waxes from leaf surfaces by simulated rain. New Phytol. 102 (1), 161–173.Google Scholar
Beard, K. V. 1976 Terminal velocity and shape of cloud and precipitation drops aloft. J. Atmos. Sci. 33 (5), 851–864.Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic Press.Google Scholar
Coleman, H. W. & Steele, W. G. 2009 Experimentation, Validation, and Uncertainty Analysis for Engineers. Wiley.Google Scholar
Dean, R., Nelson, D. F., Brown, M. L., Couch, R. W. & Blanchard, M. W.2008 Method and apparatus for forming high-speed liquid. US Patent 7,380,918.Google Scholar
Dickerson, A. K., Shankles, P. G., Madhavan, N. M. & Hu, D. L. 2012 Mosquitoes survive raindrop collisions by virtue of their low mass. Proc. Natl Acad. Sci. USA 109 (25), 9822–9827.Google Scholar
Dorf, R. C. 2004 The Engineering Handbook. CRC press.Google Scholar
Eggers, J., Fontelos, M. A., Josserand, C. & Zaleski, S. 2010 Drop dynamics after impact on a solid wall: theory and simulations. Phys. Fluids 22 (6), 062101.Google Scholar
Fyall, A. A. 1966 Practical aspects of rain erosion of aircraft and missiles. Phil. Trans. R. Soc. Lond. A 260 (1110), 161–167.Google Scholar
Gordillo, L., Sun, T.-P. & Cheng, X. 2018 Dynamics of drop impact on solid surfaces: evolution of impact force and self-similar spreading. J. Fluid Mech. 840, 190–214.Google Scholar
Grinspan, A. S. & Gnanamoorthy, R. 2010 Impact force of low velocity liquid droplets measured using piezoelectric pvdf film. Colloids Surf. A 356 (1), 162–168.Google Scholar
Haferl, S. & Poulikakos, D. 2003 Experimental investigation of the transient impact fluid dynamics and solidification of a molten microdroplet pile-up. Intl J. Heat Mass Transfer 46 (3), 535–550.Google Scholar
Haley, P. J. & Miksis, M. J. 1991 The effect of the contact line on droplet spreading. J. Fluid Mech. 223, 57–81.Google Scholar
Haller, K. K., Poulikakos, D., Ventikos, Y. & Monkewitz, P. 2003 Shock wave formation in droplet impact on a rigid surface: lateral liquid motion and multiple wave structure in the contact line region. J. Fluid Mech. 490, 1–14.Google Scholar
Haller, K. K., Ventikos, Y., Poulikakos, D. & Monkewitz, P. 2002 Computational study of high-speed liquid droplet impact. J. Appl. Phys. 92 (5), 2821–2828.Google Scholar
Huang, L., Folkes, J., Kinnell, P. & Shipway, P. H. 2012 Mechanisms of damage initiation in a titanium alloy subjected to water droplet impact during ultra-high pressure plain waterjet erosion. J. Mater. Process. Technol. 212 (9), 1906–1915.Google Scholar
Josserand, C. & Thoroddsen, S. T. 2016 Drop impact on a solid surface. Annu. Rev. Fluid Mech. 48, 365–391.Google Scholar
Josserand, C. & Zaleski, S. 2003 Droplet splashing on a thin liquid film. Phys. Fluids 15 (6), 1650–1657.Google Scholar
Lagubeau, G., Fontelos, M. A., Josserand, C., Maurel, A., Pagneux, V. & Petitjeans, P. 2012 Spreading dynamics of drop impacts. J. Fluid Mech. 713, 50–60.Google Scholar
Li, J., Zhang, B., Guo, P. & Lv, Q. 2014 Impact force of a low speed water droplet colliding on a solid surface. J. Appl. Phys. 116 (21), 214903.Google Scholar
Marshall, H. P., Conway, H. & Rasmussen, L. A. 1999 Snow densification during rain. Cold Reg. Sci. Technol. 30 (1), 35–41.Google Scholar
Mitchell, B. R., Bate, T. E., Klewicki, J. C., Korkolis, Y. P. & Kinsey, B. L. 2017 Experimental investigation of droplet impact on metal surfaces in reduced ambient pressure. Procedia Manufacturing 10, 730–736.Google Scholar
Mitchell, B. R., Nassiri, A., Locke, M. R., Klewicki, J. C., Korkolis, Y. P. & Kinsey, B. L. 2016 Experimental and numerical framework for study of low velocity water droplet impact dynamics. In ASME 2016 11th International Manufacturing Science and Engineering Conference, American Society of Mechanical Engineers.Google Scholar
Mongruel, A., Daru, V., Feuillebois, F. & Tabakova, S. 2009 Early post-impact time dynamics of viscous drops onto a solid dry surface. Phys. Fluids 21 (3), 032101.Google Scholar
Nearing, M. A., Bradford, J. M. & Holtz, R. D. 1986 Measurement of force versus time relations for waterdrop impact. Soil Sci. Soc. Am. 50 (6), 1532–1536.Google Scholar
Ortega-Jimenez, V. M., Badger, M., Wang, H. & Dudley, R. 2016 Into rude air: hummingbird flight performance in variable aerial environments. Phil. Trans. R. Soc. Lond. B 371, 20150387.Google Scholar
Philippi, J., Lagrée, P. & Antkowiak, A. 2016 Drop impact on a solid surface: short-time self-similarity. J. Fluid Mech. 795, 96–135.Google Scholar
Pizzola, P. A., Roth, S. & De Forest, P. R. 1986 Blood droplet dynamics i. J. Forensic Sci. 31 (1), 36–49.Google Scholar
Riboux, G. & Gordillo, J. M. 2014 Experiments of drops impacting a smooth solid surface: A model of the critical impact speed for drop splashing. Phys. Rev. Lett. 113 (2), 024507.Google Scholar
Rioboo, R., Marengo, M. & Tropea, C. 2002 Time evolution of liquid drop impact onto solid, dry surfaces. Exp. Fluids 33 (1), 112–124.Google Scholar
Roisman, I. V. 2009 Inertia dominated drop collisions. ii. an analytical solution of the Navier–Stokes equations for a spreading viscous film. Phys. Fluids 21 (5), 052104.Google Scholar
Roisman, I. V., Berberović, E. & Tropea, C. 2009 Inertia dominated drop collisions. i. on the universal flow in the lamella. Phys. Fluids 21 (5), 052103.Google Scholar
Römkens, M. J. M., Helming, K. & Prasad, S. N. 2002 Soil erosion under different rainfall intensities, surface roughness, and soil water regimes. Catena 46 (2), 103–123.Google Scholar
Saylor, J. R. & Jones, B. K. 2005 The existence of vortices in the wakes of simulated raindrops. Phys. Fluids 17 (3), 031706.Google Scholar
Šikalo, Š., Marengo, M., Tropea, C. & Ganić, E. N. 2002 Analysis of impact of droplets on horizontal surfaces. Expl Therm. Fluid Sci. 25 (7), 503–510.Google Scholar
Šikalo, Š., Tropea, C. & Ganić, E. N. 2005 Dynamic wetting angle of a spreading droplet. Expl. Therm. Fluid Sci. 29 (7), 795–802.Google Scholar
Szakáll, M., Mitra, S. K., Diehl, K. & Borrmann, S. 2010 Shapes and oscillations of falling raindrops. Atmospheric Res. 97 (4), 416–425.Google Scholar
Taylor, T. D. & Acrivos, A. 1964 On the deformation and drag of a falling viscous drop at low reynolds number. J. Fluid Mech. 18 (3), 466–476.Google Scholar
Thoraval, M.-J., Takehara, K., Etoh, T. G., Popinet, S., Ray, P., Josserand, C., Zaleski, S. & Thoroddsen, S. T. 2012 von Kármán vortex street within an impacting drop. Phys. Rev. Lett. 108 (26), 264506.Google Scholar
Thoroddsen, S. T. & Sakakibara, J. 1998 Evolution of the fingering pattern of an impacting drop. Phys. Fluids 10 (6), 1359–1374.Google Scholar
Trefethen, L. 1969 Surface tension in fluid mechanics. Lubricating Oil 25, 35–38.Google Scholar
Tsai, P., Pacheco, S., Pirat, C., Lefferts, L. & Lohse, D. 2009 Drop impact upon micro- and nanostructured superhydrophobic surfaces. Langmuir 25 (20), 12293–12298.Google Scholar
Weiss, D. A. & Yarin, A. L. 1999 Single drop impact onto liquid films: neck distortion, jetting, tiny bubble entrainment, and crown formation. J. Fluid Mech. 385, 229–254.Google Scholar
Wildeman, S., Visser, C. W., Sun, C. & Lohse, D. 2016 On the spreading of impacting drops. J. Fluid Mech. 805, 636–655.Google Scholar
Xu, L., Zhang, W. W. & Nagel, S. R. 2005 Drop splashing on a dry smooth surface. Phys. Rev. Lett. 94 (18), 184505.Google Scholar
Yarin, A. L. & Weiss, D. A. 1995 Impact of drops on solid surfaces: self-similar capillary waves, and splashing as a new type of kinematic discontinuity. J. Fluid Mech. 283, 141–173.Google Scholar
Yu, Y. & Hopkins, C. 2018 Experimental determination of forces applied by liquid water drops at high drop velocities impacting a glass plate with and without a shallow water layer using wavelet deconvolution. Exp. Fluids 59, 1–23.Google Scholar
Zhang, B., Li, J., Guo, P. & Lv, Q. 2017 Experimental studies on the effect of Reynolds and weber numbers on the impact forces of low-speed droplets colliding with a solid surface. Exp. Fluids 58 (9), 125.Google Scholar
Supplementary material: File

Mitchell et al. supplementary material

Mitchell et al. supplementary material 1

Download Mitchell et al. supplementary material(File)
File 3.6 MB