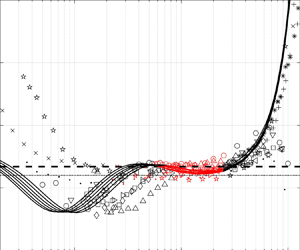
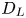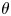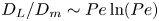doi:10.1017/jfm.2024.1073 Balasubramanian et al. Bursting bubble in an elastoviscoplastic medium
JFM Rapids
The vertical-velocity skewness in the inertial sublayer of turbulent wall flows
-
- Published online by Cambridge University Press:
- 18 December 2024, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scaling laws and mechanisms of hydrodynamic dispersion in porous media
-
- Published online by Cambridge University Press:
- 19 December 2024, R2
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
Transition to turbulence in the wide-gap spherical Couette system
-
- Published online by Cambridge University Press:
- 05 December 2024, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parametric study and scaling of a minijet-manipulated supersonic jet
-
- Published online by Cambridge University Press:
- 05 December 2024, A2
-
- Article
-
- You have access
- HTML
- Export citation
The wind-shade roughness model for turbulent wall-bounded flows
-
- Published online by Cambridge University Press:
- 11 December 2024, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Imbibition dynamics in a flattened triangular channel including corner film flow
-
- Published online by Cambridge University Press:
- 05 December 2024, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kinetic modelling of rarefied gas mixtures with disparate mass in strong non-equilibrium flows
-
- Published online by Cambridge University Press:
- 05 December 2024, A5
-
- Article
-
- You have access
- HTML
- Export citation
Wave scattering by plate array metacylinders of arbitrary cross-section
-
- Published online by Cambridge University Press:
- 05 December 2024, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free-surface effects on the flow around two circular cylinders in tandem
-
- Published online by Cambridge University Press:
- 05 December 2024, A7
-
- Article
-
- You have access
- HTML
- Export citation
A swimming bacterium in a two-fluid model of a polymer solution
-
- Published online by Cambridge University Press:
- 05 December 2024, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bursting bubble in an elastoviscoplastic medium
-
- Published online by Cambridge University Press:
- 05 December 2024, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eulerian–Lagrangian direct numerical simulation of turbulence modulation in a compressible multiphase transverse jet
-
- Published online by Cambridge University Press:
- 05 December 2024, A10
-
- Article
-
- You have access
- HTML
- Export citation
Active noise control of a supersonic underexpanded planar jet guided by resolvent analysis
-
- Published online by Cambridge University Press:
- 05 December 2024, A11
-
- Article
-
- You have access
- HTML
- Export citation
An enthalpy-based model for the physics of ice-crystal icing
-
- Published online by Cambridge University Press:
- 06 December 2024, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A diffusion-based wind turbine wake model
-
- Published online by Cambridge University Press:
- 06 December 2024, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A long-wave model for a falling upper convected Maxwell film inside a tube
-
- Published online by Cambridge University Press:
- 06 December 2024, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Plateau–Rayleigh instability in a capillary: assessing the importance of inertia
-
- Published online by Cambridge University Press:
- 11 December 2024, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A mathematical model for the interaction of anisotropic turbulence with porous surfaces
-
- Published online by Cambridge University Press:
- 09 December 2024, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A shear and elongational decomposition approach of the rate-of-deformation tensor for non-Newtonian flows with mixed kinematics
-
- Published online by Cambridge University Press:
- 10 December 2024, A17
-
- Article
-
- You have access
- HTML
- Export citation
The dynamics of concentration fluctuations within passive scalar plumes in a turbulent neutral boundary layer
-
- Published online by Cambridge University Press:
- 09 December 2024, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation