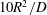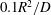Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 127
Leading-edge receptivity of a hypersonic boundary layer on a flat plate
-
- Published online by Cambridge University Press:
- 12 January 2001, pp. 73-94
-
- Article
- Export citation
- Cited by 127
On the mathematics of fluidization Part 2. Steady motion of fully developed bubbles
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 57-80
-
- Article
- Export citation
- Cited by 127
A numerical study of laminar separation bubbles using the Navier-Stokes equations
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 713-736
-
- Article
- Export citation
- Cited by 127
Direct numerical simulation of stenotic flows. Part 2. Pulsatile flow
-
- Published online by Cambridge University Press:
- 14 June 2007, pp. 281-318
-
- Article
- Export citation
- Cited by 127
Motion of a sphere in the presence of a plane interface. Part 1. An approximate solution by generalization of the method of Lorentz
-
- Published online by Cambridge University Press:
- 19 April 2006, pp. 705-726
-
- Article
- Export citation
- Cited by 127
Turbulent boundary layers over permeable walls: scaling and near-wall structure
-
- Published online by Cambridge University Press:
- 10 October 2011, pp. 141-170
-
- Article
- Export citation
- Cited by 127
Numerical solution for the flow around a cylinder at Reynolds numbers of 40, 200 and 500
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 369-386
-
- Article
- Export citation
- Cited by 127
On the prediction of intermittent turbulent flows
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 273-295
-
- Article
- Export citation
- Cited by 127
A general theory for two-dimensional vortex interactions
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 269-303
-
- Article
- Export citation
- Cited by 127
Three-dimensional filling flow into a model left ventricle
-
- Published online by Cambridge University Press:
- 05 September 2005, pp. 179-198
-
- Article
- Export citation
- Cited by 127
On the direct initiation of gaseous detonations by an energy source
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 227-248
-
- Article
- Export citation
- Cited by 127
Topological constraints associated with fast dynamo action
-
- Published online by Cambridge University Press:
- 20 April 2006, pp. 493-507
-
- Article
- Export citation
- Cited by 127
The transverse force on clean and contaminated bubbles rising near a vertical wall at moderate Reynolds number
-
- Published online by Cambridge University Press:
- 11 November 2003, pp. 235-253
-
- Article
- Export citation
- Cited by 126
Quantitative measurements of three-dim ensional structures in the wake of a circular cylinder
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 277-296
-
- Article
- Export citation
- Cited by 126
Approach to transverse uniformity of concentration distribution of a solute in a solvent flowing along a straight pipe
-
- Published online by Cambridge University Press:
- 06 February 2014, pp. 196-213
-
- Article
- Export citation
- Cited by 126
Shear-induced self-diffusion in non-colloidal suspensions
-
- Published online by Cambridge University Press:
- 28 April 2004, pp. 285-314
-
- Article
- Export citation
- Cited by 126
A study of forces, circulation and vortex patterns around a circular cylinder in oscillating flow
-
- Published online by Cambridge University Press:
- 21 April 2006, pp. 467-494
-
- Article
- Export citation
- Cited by 126
Three-dimensional direct numerical simulation of wake transitions of a circular cylinder
-
- Published online by Cambridge University Press:
- 25 July 2016, pp. 353-391
-
- Article
- Export citation
- Cited by 126
Nonlinear deformation and breakup of stretching liquid bridges
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 207-245
-
- Article
- Export citation
- Cited by 126
Development of coherent structures in concentrated suspensions of swimming model micro-organisms
-
- Published online by Cambridge University Press:
- 25 November 2008, pp. 401-431
-
- Article
- Export citation