The distribution of visits to a particular gene frequency in a finite population of size N with non-overlapping generations is derived. It is shown, by using well-known results from the theory of finite Markov chains, that all such distributions are geometric, with parameters dependent only on the set of bij's, where bij is the mean number of visits to frequency j/2N, given initial frequency i/2N. The variance of such a distribution does not agree with the value suggested by the diffusion method. An improved approximation is derived.

A deterministic model of cyclical selection in randomly mating populations is studied. Sufficient conditions for a protected polymorphism, which are for the special case of alternating selection also necessary conditions, are obtained using a simple graphical approach. The most important condition requires ‘marginal overdominance’ (Wallace, 1968); the other conditions seem hard to satisfy in a natural situation. Furthermore it is shown that the cyclical selection model can be regarded as a special case of a frequency-dependent selection model (Cockerham et al. 1972). Using this property, a mean fitness function for the cyclical selection model is derived. Generally, the mean fitness will not be maximized under cyclical selection. The relevance of the model to the problem of the role of cyclical selection in the maintenance of genetic polymorphism in natural populations is discussed. It is concluded that this relevance is probably rather limited with regard to the creation of protected polymorphism, but that the influence of cyclical selection on transient polymorphisms might be more significant. An approximate formula for the time needed for a given change in gene frequency under cyclical selection is derived. It appears that cyclical selection can extend considerably the time during which a transient polymorphism persists, especially if the selective differences in the different environments are of the same order of magnitude and of opposite sign.

Trimethoprim-resistant mutants of E. coli K12 have been isolated by-serial subculture in progressively higher concentrations of trimethoprim. High-level resistance depends on the accumulation of several mutational changes. Transduction with bacteriophage P1 has shown that all the mutations involved in resistance are associated with a locus, to be called tmr, between pyr A and pdxA and closely linked to pdxA. Resistance is accompanied by, and presumably due to, an increased activity of the target enzyme, dihydrofolate reductase. The tmr locus may include the structural gene for dihydrofolate reductase but the only mutations that have so far been observed are concerned with regulation.

The order of replication of a series of genes in Pseudomonas aeruginosa has been studied in synchronized cultures using a method based on the technique of sequential mutagenesis. This technique relies on the increased susceptibility of the replication point of the bacterial chromosome to mutagenesis by N-methyl-N′-nitro-N-nitrosoguanidine. The genes studied were those previously mapped by conjugation and whose order of replication had been studied by an investigation of gene frequencies in exponential populations. The results are consistent with the idea that there is two-way replication of the chromosome of P. aeruginosa starting at a point near trp-1 and arg-6. They also confirm that the two linkage groups which have been found by conjugation replicate at different times. If the assumption is made that there is only one chromosome in P. aeruginosa, the results can be used to show how the two linkage groups may possibly be joined together and the order is such that there would have to be two sites of attachment for the sex factor FP2.

An experiment was carried out to test the effect of varying selection intensity on the response to individual selection with a fixed number of individuals scored per generation. The selected trait was egg laying of virgin females of Tribolium castaneum scored from the 7th to the 1 lth day after adult emergence. Five different selected proportions of females were considered (5, 10, 20, 33 and 50%) and each treatment was represented by two replicate lines. Control lines were maintained throughout the experiment. The lines selected at the lowest proportions (5 and 10%) led to the largest initial gains, but the largest final gains were achieved, by the lines where the proportions selected were 10 and 20%, in agreement with theory. Lines where the proportion selected was 50% gave the lowest rate of response over the period considered (32 generations). A good agreement was found between predicted and realized short-term responses to selection. Prediction at later stages of selection deteriorated in the most strongly selected lines mainly due to the levels of inbreeding attained.

Wild-type strains of Coprinus lagopus are sensitive to para-fluoro-phenylalanine and ethionine. Resistant mutants to these two analogues are known but all these mutants are recessive in a heterozygous dikaryon except for F7 (pfpr-3) which is semi-dominant. Resistance to two other analogues, however – canavanine sulphate and azetidine-2-carboxylic acid – were found to be wild-type features. One strain of C. lagopus sensitive to canavanine was identified. Selection for canavanine resistance in monokaryons always yielded only dominant resistance, while selection for para-fluorophenylalanine resistance in monokaryons gave only recessive resistance. Canavanine-resistant mutants were due to a single gene mutation which, like the wild-type resistance, were dominant in heterozygous dikaryons. The wild-type resistance was also dominant in a diploid but the mutant resistance was recessive. Selection for resistance to para-fluorophenylalanine in auxotrophically balanced dikaryons resulted in the identification of two new loci (pfpr-10 and pfpr-ll), and two specific dominance modifiers (mod+-10 and mod+-ll). In the absence of the specific modifier, pfpr-10 and pfpr-ll were recessive while, in the presence of even one dose of the specific modifier, resistance was dominant in the dikaryon. The pfpr-10 and pfpr-ll even in the presence of two doses of modifier were fully recessive in the diploid. The action of the modifier genes and the reversal of dominance in dikaryon and diploid is discussed in terms of negative complementation in an oligomeric product of the pfpr gene and localized translation of the relevant mRNA in the cell with the modifier acting as a reinforcer of localization.

exrB derivatives of H/r30 and WP2 are sensitive to ultraviolet radiation (UV), methylmethane sulphonate (MMS) and will not form colonies at 42 °C. Revertants to wild type were selected by plating on either nutrient plates containing MMS or nutrient plates incubated at 42 °C. Revertants selected for MMS resistance were temperature- and UV-resistant, and all revertants selected for temperature resistance were MMS and UV resistant. The frequency with which revertants appeared on MMS plates was about eight times as high as it was at 42 °C, and the variance in frequency of revertants among cultures started with small inocula was higher on selection at 42 °C than on MMS. The spontaneous frequency was estimated to be 10−6 to 10−7, sufficiently low to suggest a single mutational event. Among wild-type revertants selected at 42 °C there was a stable and an unstable class. exrB+ could be co-transduced with malB+ from stable revertants to an exrB strain, but could not from unstable revertants. None of the revertants could support the growth of amber or ochre mutants of phage T4, nor were amber and ochre suppressed exrB strains wild type with regards MMS and temperature resistance. The presence of a polarity suppressor in an exrB strain did not modify resistance to UV or temperature. Neither UV or MMS was able to induce mutations in an exrB strain.

Using the moments of gene frequencies, the drift variances of heterozygosity and genetic distance in transient states have been studied under the assumption that all mutations are selectively neutral. Interestingly, this approach provides a simple derivation of Stewart's formula for the variance of heterozygosity at steady state. The results obtained indicate that if all alleles in the initial population are equally frequent, the standard derivation of heterozygosity is very small and increases linearly with time in the early generations. On the other hand, if the initial allele frequencies deviate appreciably from equality, then the standard deviation in the early generations is much larger but increases linearly with the square root of time. Under certain conditions, the standard deviation of genetic distance also increases linearly with time. Numerical computations have shown that the standard deviations of heterozygosity and genetic distance relative to their means are so large that a large number of loci must be used in estimating the average heterozygosity and genetic distance per locus.

Twelve FPA-resistant mutants were selected on medium containing p-fluorophenylalanine and ethionine. Dominance tests in heterozygous diploids showed that 8 out of 12 are dominant and 4 recessive to their wild-type alleles. One mutant, fpa60, showed a partial requirement for tyrosine and was found to be allelic to an fpaA mutant described previously. A tyrosine non-requirer, fpa65, was also assigned to this locus. The other 10 mutants did not show any growth requirement and were simultaneously resistant to ethionine and 3-amino-L-tyrosine. Of the 8 dominant mutants, 3 were allelic to the permease-mutants at the locus fpaD. Dominant mutants showed higher degrees of resistance than recessive ones. Six new loci, identified after preliminary genetic analysis, were located on 3 linkage groups: 3 on linkage group VI, and one each on linkage groups I, V, and VIII. The recombinant fpaD11; fpaK69 was found to be sensitive to FPA.

A considerable improvement in the selection of haploids in Aspergillus nidulans is described. Haploidization is used to assign genes to linkage groups (chromosomes) in fungi. The differential effect of a polyene antibiotic, N-glycosyl-polifungin, in respect to haploids and diploids, was utilized. In minimal medium only diploids (constructed from a ‘Master Strain’ and the investigated strain), which are fully heterozygous and thus have no growth requirements, germinate and are killed by the antibiotic. However, auxotrophic haploids, either induced or spontaneously formed, survive. These can then be used for linkage studies.

To test whether exrB, a mutation in Escherichia coli B making this strain sensitive to ultraviolet radiation and unable to divide normally, is dominant to exrB+, merodiploids were constructed by crossing Hfr exrB metA+his × F−malB met A thr proA recA. metA+recombinants were fertile (F′) and sensitive to UV. One of these, F′ exrB proA, was crossed with an F−metA malB thr, selecting for metA+proA+. All such progeny acquiring malB+ were UV-sensitive, fertile and segregated met mal UV-resistant progeny. They were, therefore, meriodiploids, F′ exrB/exrB+. exrB is dominant to exrB+, in which respect it resembles exrA (lex).

Wild-type strains of Aspergillus nidulans grow poorly on L-histidine as a sole nitrogen source. The synthesis of the enzyme histidase (EC. 4.3.1.3) appears to be a limiting factor in the growth of the wild type, as strains carrying the mutant areA102 allele have elevated histidase levels and grow strongly on histidine as a sole nitrogen source. L-Histidine is an extremely weak sole carbon source for all strains.

Ammonium repression has an important role in the regulation of histidase synthesis and the relief of ammonium repression is dependent on the availability of a good carbon source. The level of histidase synthesis does not respond to the addition of exogenous substrate.

Mutants carrying lesions in the sarA or sarB loci (suppressor of areA102) have been isolated. The growth properties of these mutants on histidine as a sole nitrogen source correlate with the levels of histidase synthesized. Mutation at the sarA and sarB loci also reduces the utilization of a number of other nitrogen sources. The data suggest that these two genes may code for regulatory products involved in nitrogen catabolism. No histidase structural gene mutants were identified and possible explanations of this are discussed.

Nine (41%) of the 22 enzymic and non-enzymic loci examined in a strain of mice divergently selected for six-week body weight (six lines selected in each direction and six controls) were found to be polymorphic. The degree of polymorphism varied between the replicates from a maximum of 38% to a minimum of 14% with an average individual heterozygous at 7·7% of its loci. There was no obvious association between any of the isozyme variants and body size. The frequency distribution among the 18 lines was adequately accounted for by random genetic drift. However, an association was observed between body size and the Hbb locus; the Hbbs allele was found to be fixed in all of the six Large lines. An examination of the variance of gene frequencies at this locus excluded random genetic drift as an explanation for the fixation.

The charge state model of Ohta & Kimura (1973) for the number of electrophoretically detectable alleles in a finite population, is extended to include mutations of both one and two charge changes. The effective number of alleles (ne) is increased only slightly by this extension. Electrophoretic profiles of neutral variants are shown on average to be leptokurtic and have their odd central moments equal to zero. The expected frequency distribution of pairs of gametes which differ by 1,2,3,… charge units can be obtained as the sum of the appropriate terms from two geometric series.

The first part of the paper provides strong supportive evidence for the previous findings (Cummins & Day, 1973; Day & Cummins, 1973) that the two alleles of the mating-type locus of the basidiomycete Ustilago violacea have different periods of inducibility during a cell cycle, and that the cell cycle characteristics of each allele are maintained in freshly isolated diploids. This difference in temporal properties of the alleles appears to be the basis of the dominance of allele a2 as it is inducible during a phase of the cell cycle when allele a1 is non-inducible. During G1 both alleles appear to be inducible and apparently ‘neutralize’ each other so that the cell cannot mate.

The second part of the paper provides evidence for a unique genetic control mechanism. The evidence suggests that the period of cell cycle inducibility of a locus governing a morphogenetic pathway may be regulated by a separate control gene the cc locus, with two known alleles ccstr(a stringent or restricted period of inducibility) and ccrel (a relaxed or non-restricted period of inducibility). This hypothesis stems from analysis of a diploid that was a1· ccstr/a2· ccrel and showed dominance of allele a2 during the S and G2 phases when freshly isolated, but which became incapable of mating after a period of subculturing. Analysis of haploids derived from this diploid strain showed that both mating-type alleles were functional but that it was now homozygous for ccstr, i.e. of genotype a1· ccstr/a2·ccstr· Thus the temporal and functional aspects of the mating type alleles are determined by different loci. It is postulated that cell cycle control loci may be widespread and serve to regulate the action of genes concerned with morphogenesis in relation to other cell cycle events.

Ethidium bromide and acriflavin-resistant mutants of petite-negative yeast Kluyveromyces lactis were prepared. One kind of nuclear mutation (EBR1) gave resistance to ethidium bromide and correlated sensitivity towards acriflavin. Another nuclear mutation (EBR2) did not affect ‘natural’ resistance of this yeast towards 15 μM acriflavin. Both nuclear mutations mapped at different loci, suggesting lack of linkage. Cytoplasmic mutants resistant to these two drugs were unstable when grown in complete media with dextrose, reverting to a wild-type resistance genotype. When grown in glycerol-containing media these mutants maintained their cytoplasmic drug-resistance conferring factors.

This paper describes the results of an experiment to measure the effect on mean population fitness of recombination in the second chromosome of Drosophila melanogaster. There was a small and non-significant effect of recombination in lowering egg-to-adult viability of heterozygotes for wild-type chromosomes. A large (7%) and significant effect of recombinant chromosomes on the fecundity of Cy female carriers was detected.

The model, suggested by Ohta & Kimura, of an infinite number of selectively neutral alleles, in which alleles can only mutate to neighbouring alleles, has been extended to include a migratory pattern. The stepping-stone and island models of migration have been considered. In the latter case, it has been found that as the number of colonies becomes large, the expected number of alleles, ne, becomes approximately equal to

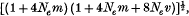
where m is the migration rate, v is the mutation rate and Ne is the effective size of each population. This solution tends to that of Ohta & Kimura as m → 0 but one can see that for any appreciable value of Nem, a large increase in ne is obtained. In order to check the validity of iterative results, models with a finite number of alleles have been considered, and their solutions have been found to converge quickly to those of the infinite case. The results exemplify the great power of migratory structure and neutral alleles to maintain a large amount of heterozygosity. Double step mutation and the finite time solution have also been considered.

Plasmid-mediated sensitivity to filamentous phage IKe is shown to be a property exclusive to plasmids of the N incompatibility group. As with other sex factor-specific phages, IKe sensitivity results from the provision of a plasmid-encoded receptor. However, direct evidence for IKe adsorption to a sex pilus-like structure is so far lacking.

Mutations in an N plasmid were obtained which affected IKe infect-ability and N transfer frequency simultaneously, though to different extents. IKe receptors could be removed to a limited extent by high speed blending, but only under more extreme conditions (higher speed and in low ionic strength medium) than F pili. As with F-specific filamentous phages, IKe adsorption was partially blocked by Zn2+.

We tentatively suggest that the results accord with the IKe receptor being a sex pilus rather different from F and I pili (possibly in being much shorter in liquid culture), but other interpretations of these data are possible.

Sorting out of cytoplasm determinants can be achieved in Podospora anserina by the use of protoplasts. In this way four cytoplasmic mutations have been isolated. These mutations affect a precise stage of development of the fungus. In crosses with wild-type strains, the mutants show maternal inheritance when no cytoplasmic contact precedes fertilization. However, when cytoplasmic mixing occurs before fertilization, the cytoplasmic wild-type factor shows dominant and/or suppressive properties over the mutant factor.