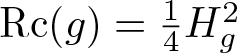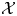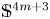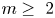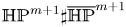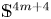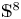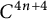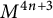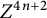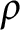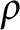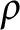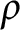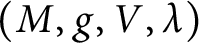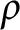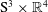61 results
Generalized Ricci flow on aligned homogeneous spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 226-246
-
- Article
-
- You have access
- HTML
- Export citation
Sharp bounds on the height of K-semistable Fano varieties I, the toric case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 10 October 2024, pp. 2366-2406
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On conformally flat minimal Legendrian submanifolds in the unit sphere
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
On almost quotient Yamabe solitons
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 479-493
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Positive Einstein metrics with
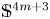 $\mathbb {S}^{4m+3}$ as the principal orbit
$\mathbb {S}^{4m+3}$ as the principal orbit
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1004-1040
- Print publication:
- May 2024
-
- Article
-
- You have access
- HTML
- Export citation
Calibrated geometry in hyperkähler cones, 3-Sasakian manifolds, and twistor spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure of generalized Yamabe solitons and its applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 336-348
-
- Article
-
- You have access
- HTML
- Export citation
A note on almost Yamabe solitons
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 183-187
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
Classification of generalized Einstein metrics on three-dimensional Lie groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. 2038-2095
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Second-order estimates for collapsed limits of Ricci-flat Kähler metrics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 912-926
- Print publication:
- September 2023
-
- Article
- Export citation
Bismut Ricci flat manifolds with symmetries
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 26 July 2022, pp. 1371-1390
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On cohomogeneity one Hermitian non-Kähler metrics
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 17 February 2022, pp. 545-587
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some characterizations of
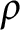 $\rho $
-Einstein solitons on Sasakian manifolds
$\rho $
-Einstein solitons on Sasakian manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 1036-1049
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE CLASSIFICATION OF NONCOMPACT QUASI-EINSTEIN MANIFOLDS WITH VANISHING CONDITION ON THE WEYL TENSOR
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 07 May 2021, pp. 336-346
- Print publication:
- May 2022
-
- Article
- Export citation
FOUR-MANIFOLDS WITH POSITIVE CURVATURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 06 April 2020, pp. 245-257
- Print publication:
- May 2021
-
- Article
- Export citation
EXISTENCE AND COMPACTNESS THEORY FOR ALE SCALAR-FLAT KÄHLER SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 10 January 2020, e1
-
- Article
-
- You have access
- Open access
- Export citation
Nearly Parallel G2-structures with Large Symmetry Group
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 16 December 2019, pp. 339-359
- Print publication:
- April 2021
-
- Article
- Export citation
Einstein–Maxwell Equations on Four-dimensional Lie Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 09 May 2019, pp. 822-840
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Yamabe Solitons and Ricci Solitons on Almost co-Kähler Manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 07 May 2019, pp. 653-661
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Ricci Solitons on Almost Co-Kähler Manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 07 December 2018, pp. 912-922
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation