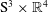Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Singhal, Ragini
2024.
Nearly half-flat SU(3) structures on S3 × S3.
Differential Geometry and its Applications,
Vol. 97,
Issue. ,
p.
102187.
Alonso, Izar
2025.
Coclosed $$G_2$$-structures on $$\text {SU}(2)^2$$-invariant cohomogeneity one manifolds.
Annals of Global Analysis and Geometry,
Vol. 67,
Issue. 1,