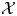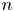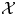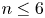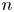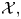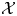1. Introduction
1.1 The height of K-semistable Fano varieties
Let ![]() $(\mathcal {X},\mathcal {L})$ be a projective flat scheme
$(\mathcal {X},\mathcal {L})$ be a projective flat scheme ![]() $\mathcal {X}$ over
$\mathcal {X}$ over ![]() $\mathbb {Z}$ of relative dimension
$\mathbb {Z}$ of relative dimension ![]() $n,$ endowed with a relatively ample line bundle
$n,$ endowed with a relatively ample line bundle ![]() $\mathcal {L}$. The complexification of
$\mathcal {L}$. The complexification of ![]() $(\mathcal {X},\mathcal {L})$ will be denoted by
$(\mathcal {X},\mathcal {L})$ will be denoted by ![]() $(X,L)$. In other words,
$(X,L)$. In other words, ![]() $X$ is the complex projective variety consisting of the complex points of
$X$ is the complex projective variety consisting of the complex points of ![]() $\mathcal {X}$ and
$\mathcal {X}$ and ![]() $L$ is the corresponding ample line bundle over
$L$ is the corresponding ample line bundle over ![]() $X$.
$X$.
A central role in arithmetic and Diophantine geometry is played by the height of ![]() $(\mathcal {X},\mathcal {L}),$ which is defined with respect to a continuous metric
$(\mathcal {X},\mathcal {L}),$ which is defined with respect to a continuous metric ![]() $\Vert \cdot \Vert$ on
$\Vert \cdot \Vert$ on ![]() $L$. This is an arithmetic analog of the algebro-geometric degree of
$L$. This is an arithmetic analog of the algebro-geometric degree of ![]() $(X,L),$ i.e. of the top intersection number
$(X,L),$ i.e. of the top intersection number ![]() $L^{n}$ on
$L^{n}$ on ![]() $X$. The height of
$X$. The height of ![]() $(\mathcal {X},\mathcal {L},\Vert \cdot \Vert )$ – also known as the Faltings height – is defined as the
$(\mathcal {X},\mathcal {L},\Vert \cdot \Vert )$ – also known as the Faltings height – is defined as the ![]() $(n+1)$-fold arithmetic intersection number of the metrized line bundle
$(n+1)$-fold arithmetic intersection number of the metrized line bundle ![]() $(\mathcal {L}, \Vert \cdot \Vert )$ on
$(\mathcal {L}, \Vert \cdot \Vert )$ on ![]() $\mathcal {X},$ introduced by Gillet and Soulé in the context of Arakelov geometry [Reference FaltingsFal91, Reference Bost, Gillet and SouléBGS94] (see § 1.1). We recall that in Arakelov geometry the metric
$\mathcal {X},$ introduced by Gillet and Soulé in the context of Arakelov geometry [Reference FaltingsFal91, Reference Bost, Gillet and SouléBGS94] (see § 1.1). We recall that in Arakelov geometry the metric ![]() $\Vert \cdot \Vert$ on
$\Vert \cdot \Vert$ on ![]() $L$ plays the role of a ‘compactification’ of
$L$ plays the role of a ‘compactification’ of ![]() $\mathcal {X}$. Accordingly, a metrized line bundle
$\mathcal {X}$. Accordingly, a metrized line bundle ![]() $(\mathcal {L}, \Vert \cdot \Vert )$ is usually denoted by
$(\mathcal {L}, \Vert \cdot \Vert )$ is usually denoted by ![]() $\overline {\mathcal {L}}$. The definition of height naturally extends to any
$\overline {\mathcal {L}}$. The definition of height naturally extends to any ![]() $\mathbb {Q}$-line bundle
$\mathbb {Q}$-line bundle ![]() $\mathcal {L},$ using homogeneity.
$\mathcal {L},$ using homogeneity.
In contrast to the algebro-geometric degree of ![]() $L$, the height of
$L$, the height of ![]() $\overline {\mathcal {L}}$ can rarely be computed explicitly and all one can hope for, in general, is explicit bounds on the height. When
$\overline {\mathcal {L}}$ can rarely be computed explicitly and all one can hope for, in general, is explicit bounds on the height. When ![]() $\mathcal {L}$ is the relative canonical line bundle, which we shall denote by
$\mathcal {L}$ is the relative canonical line bundle, which we shall denote by ![]() $\mathcal {K}_{\mathcal {X}}$ and
$\mathcal {K}_{\mathcal {X}}$ and ![]() $n=1,$ such conjectural upper bounds are motivated by the Bogolomov–Miyaoka–Yau inequality on
$n=1,$ such conjectural upper bounds are motivated by the Bogolomov–Miyaoka–Yau inequality on ![]() $X\!$ and imply, in particular, the effective Mordell conjecture, concerning explicit upper bounds on the number of rational points on
$X\!$ and imply, in particular, the effective Mordell conjecture, concerning explicit upper bounds on the number of rational points on ![]() $X_{\mathbb {Q}}$, and the abc conjecture [Reference ParshinPar88, Reference VojtaVoj88, Reference SouléSou94]. Here we shall be concerned with the opposite situation where
$X_{\mathbb {Q}}$, and the abc conjecture [Reference ParshinPar88, Reference VojtaVoj88, Reference SouléSou94]. Here we shall be concerned with the opposite situation where ![]() $\mathcal {X}$ is an arithmetic Fano variety, in the sense that the relative anti-canonical line bundle is defined as a relative ample
$\mathcal {X}$ is an arithmetic Fano variety, in the sense that the relative anti-canonical line bundle is defined as a relative ample ![]() $\mathbb {Q}$-line bundle that we denote by
$\mathbb {Q}$-line bundle that we denote by ![]() $\mathcal {-K}_{\mathcal {X}},$ using additive notation for tensor products (see § 2.2.1). In particular,
$\mathcal {-K}_{\mathcal {X}},$ using additive notation for tensor products (see § 2.2.1). In particular, ![]() $X\!$ is a complex Fano variety, a variety whose canonical line bundle
$X\!$ is a complex Fano variety, a variety whose canonical line bundle ![]() $-K_{X\!}$ defines an ample
$-K_{X\!}$ defines an ample ![]() $\mathbb {Q}$-line bundle. We will also, for simplicity, assume that
$\mathbb {Q}$-line bundle. We will also, for simplicity, assume that ![]() $X\!$ is normal. As shown in [Reference Berman and BerndtssonBB17] in the toric case and then in [Reference FujitaFuj18] in general, for any complex Fano variety
$X\!$ is normal. As shown in [Reference Berman and BerndtssonBB17] in the toric case and then in [Reference FujitaFuj18] in general, for any complex Fano variety ![]() $X\!$,
$X\!$,
under the assumption that ![]() $X\!$ is K-semistable. Moreover, equality holds if and only if
$X\!$ is K-semistable. Moreover, equality holds if and only if ![]() $X=\mathbb {P}_{\mathbb {C}}^{n}$ [Reference LiuLiu18]. In contrast, when
$X=\mathbb {P}_{\mathbb {C}}^{n}$ [Reference LiuLiu18]. In contrast, when ![]() $X\!$ is not K-semistable the degree
$X\!$ is not K-semistable the degree ![]() $(-K_{X}\!)^{n}$ can be arbitrarily large in any given dimension
$(-K_{X}\!)^{n}$ can be arbitrarily large in any given dimension ![]() $n,$ for singular
$n,$ for singular ![]() $X\!$ (see [Reference DebarreDeb03, Ex 4.2] for simple two-dimensional toric examples). The notion of K-stability first arose in the context of the Yau–Tian–Donaldson conjecture for Fano manifolds, saying that a Fano manifold admits a Kähler–Einstein metric if and only if it is K-polystable [Reference TianTia97, Reference DonaldsonDon02]. The conjecture was settled in [Reference Chen, Donaldson and SunCDS15] and very recently also established for singular Fano varieties [Reference LiLi22, Reference Liu, Xu and ZhuangLXZ22]. From a purely algebro-geometric perspective K-stability can be viewed as a limiting form of Chow and Hilbert–Mumford stability [Reference Ross and ThomasRT07], which enables a good theory of moduli spaces (see the survey [Reference XuXu21]).
$X\!$ (see [Reference DebarreDeb03, Ex 4.2] for simple two-dimensional toric examples). The notion of K-stability first arose in the context of the Yau–Tian–Donaldson conjecture for Fano manifolds, saying that a Fano manifold admits a Kähler–Einstein metric if and only if it is K-polystable [Reference TianTia97, Reference DonaldsonDon02]. The conjecture was settled in [Reference Chen, Donaldson and SunCDS15] and very recently also established for singular Fano varieties [Reference LiLi22, Reference Liu, Xu and ZhuangLXZ22]. From a purely algebro-geometric perspective K-stability can be viewed as a limiting form of Chow and Hilbert–Mumford stability [Reference Ross and ThomasRT07], which enables a good theory of moduli spaces (see the survey [Reference XuXu21]).
Is there an arithmetic analog of inequality (1.1)? More precisely, it seems natural to ask if, under appropriate assumptions, the height ![]() $(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ is bounded from above by the height
$(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ is bounded from above by the height ![]() $(\overline {-\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n}}})^{n+1}$ of the relative anti-canonical line bundle on the projective space
$(\overline {-\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n}}})^{n+1}$ of the relative anti-canonical line bundle on the projective space ![]() $\mathbb {P}_{\mathbb {Z}}^{n}$ over the integers, endowed with its standard Kähler–Einstein metric (the Fubini–Study metric). This would yield an explicit bound on the height
$\mathbb {P}_{\mathbb {Z}}^{n}$ over the integers, endowed with its standard Kähler–Einstein metric (the Fubini–Study metric). This would yield an explicit bound on the height ![]() $(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$, since the height of Fubini–Study metric on projective space was explicitly calculated in [Reference Gillet and SouléGS90, § 5.4], giving, after volume normalization,
$(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$, since the height of Fubini–Study metric on projective space was explicitly calculated in [Reference Gillet and SouléGS90, § 5.4], giving, after volume normalization,
 \begin{equation} \big(\overline{-\mathcal{K}_{\mathbb{P}_{\mathbb{Z}}^{n}}}\big)^{n+1}=\frac{1}{2}(n+1)^{n+1} \Biggl((n+1)\sum_{k=1}^{n}k^{-1}-n+\log\biggl(\frac{\pi^{n}}{n!}\biggr)\Biggr). \end{equation}
\begin{equation} \big(\overline{-\mathcal{K}_{\mathbb{P}_{\mathbb{Z}}^{n}}}\big)^{n+1}=\frac{1}{2}(n+1)^{n+1} \Biggl((n+1)\sum_{k=1}^{n}k^{-1}-n+\log\biggl(\frac{\pi^{n}}{n!}\biggr)\Biggr). \end{equation}
However, if such a universal bound is to hold, one needs to impose a normalization condition on the metric on ![]() $-K_{X}$. Indeed,
$-K_{X}$. Indeed, ![]() $\overline {\mathcal {L}}^{n+1}$ is additively equivariant with respect to scalings of the metric. Accordingly, the metric
$\overline {\mathcal {L}}^{n+1}$ is additively equivariant with respect to scalings of the metric. Accordingly, the metric ![]() $\Vert \cdot \Vert$ on
$\Vert \cdot \Vert$ on ![]() $-K_{X\!}$ will henceforth be assumed to be volume-normalized in the sense that the corresponding volume form on
$-K_{X\!}$ will henceforth be assumed to be volume-normalized in the sense that the corresponding volume form on ![]() $X\!$ has total unit volume. As it turns out, the supremum of the height
$X\!$ has total unit volume. As it turns out, the supremum of the height ![]() $\overline {-\mathcal {K}_{\mathcal {X}}}^{n+1}$ over all volume-normalized metrics on
$\overline {-\mathcal {K}_{\mathcal {X}}}^{n+1}$ over all volume-normalized metrics on ![]() $-K_{X\!}$ with positive curvature current is finite if and only if
$-K_{X\!}$ with positive curvature current is finite if and only if ![]() $X\!$ is K-semistable (Theorem 2.5). It thus seems natural to make the following conjecture.
$X\!$ is K-semistable (Theorem 2.5). It thus seems natural to make the following conjecture.
Conjecture 1.1 Let ![]() $\mathcal {X}$ be an arithmetic Fano variety of relative dimension
$\mathcal {X}$ be an arithmetic Fano variety of relative dimension ![]() $n$ over
$n$ over ![]() $\mathbb {Z}$. If the complexification
$\mathbb {Z}$. If the complexification ![]() $X\!$ of
$X\!$ of ![]() $\mathcal {X}$ is K-semistable, then the following height inequality holds for any volume-normalized continuous metric on
$\mathcal {X}$ is K-semistable, then the following height inequality holds for any volume-normalized continuous metric on ![]() $-K_{X\!}$ with positive curvature current:
$-K_{X\!}$ with positive curvature current:
where ![]() $-K_{\mathbb {P}_{\mathbb {C}}^{n}}$ is endowed with the volume-normalized Fubini–Study metric. Moreover, if
$-K_{\mathbb {P}_{\mathbb {C}}^{n}}$ is endowed with the volume-normalized Fubini–Study metric. Moreover, if ![]() $\mathcal {X}$ is normal, equality holds if and only if
$\mathcal {X}$ is normal, equality holds if and only if ![]() $\mathcal {X}=\mathbb {P}_{\mathbb {Z}}^{n}$ and the metric is Kähler–Einstein, i.e. coincides with the Fubini–Study metric, modulo the action of an automorphism.
$\mathcal {X}=\mathbb {P}_{\mathbb {Z}}^{n}$ and the metric is Kähler–Einstein, i.e. coincides with the Fubini–Study metric, modulo the action of an automorphism.
More generally, when ![]() $\mathbb {Z}$ is replaced by the ring of integers of a number field
$\mathbb {Z}$ is replaced by the ring of integers of a number field ![]() $F,$ i.e. a finite field extension
$F,$ i.e. a finite field extension ![]() $F$ of
$F$ of ![]() $\mathbb {Q},$ the height
$\mathbb {Q},$ the height ![]() $(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ should be divided by the degree
$(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ should be divided by the degree ![]() $[F:\mathbb {Q}]$. But, for simplicity, we will focus on the case when
$[F:\mathbb {Q}]$. But, for simplicity, we will focus on the case when ![]() $F=\mathbb {Q}$ (see § 6.2 for a generalization of the previous conjecture). The converse ‘only if’ statement to the previous conjecture does hold (as a consequence of Theorem 2.5). Moreover, the conjecture is compatible with taking products (Proposition 2.10). The inequality in the previous conjecture is equivalent to the following inequality for any continuous metric on
$F=\mathbb {Q}$ (see § 6.2 for a generalization of the previous conjecture). The converse ‘only if’ statement to the previous conjecture does hold (as a consequence of Theorem 2.5). Moreover, the conjecture is compatible with taking products (Proposition 2.10). The inequality in the previous conjecture is equivalent to the following inequality for any continuous metric on ![]() $-K_{X\!}$ with positive curvature current, as follows from a simple scaling argument:
$-K_{X\!}$ with positive curvature current, as follows from a simple scaling argument:
 \begin{equation} \frac{\bigl(\overline{-\mathcal{K}_{\mathcal{X}}}\bigr)^{n+1}}{(n+1)}+\frac{(-K_{X}\!)^{n}}{2}\log\mu(X)\leq c_{n}, \end{equation}
\begin{equation} \frac{\bigl(\overline{-\mathcal{K}_{\mathcal{X}}}\bigr)^{n+1}}{(n+1)}+\frac{(-K_{X}\!)^{n}}{2}\log\mu(X)\leq c_{n}, \end{equation}
where ![]() $\mu (X)$ denotes the volume of
$\mu (X)$ denotes the volume of ![]() $X\!$ with respect to the measure
$X\!$ with respect to the measure ![]() $\mu$ on
$\mu$ on ![]() $X\!$ corresponding to the metric
$X\!$ corresponding to the metric ![]() $\Vert \cdot \Vert$ on
$\Vert \cdot \Vert$ on ![]() $-K_{X\!}$ and
$-K_{X\!}$ and ![]() $c_{n}$ denotes the constant in the right-hand side of formula (1.2). Some intriguing relations between the conjectural bound (1.3) and the Manin–Peyre conjecture, concerning the density of rational points on Fano varieties, are discussed in [Reference BermanBer23].
$c_{n}$ denotes the constant in the right-hand side of formula (1.2). Some intriguing relations between the conjectural bound (1.3) and the Manin–Peyre conjecture, concerning the density of rational points on Fano varieties, are discussed in [Reference BermanBer23].
Our main result concerns the case when ![]() $X\!$ is toric and
$X\!$ is toric and ![]() $\mathcal {X}$ is its canonical toric integral model (see [Reference MaillotMai00, § 2] and [Reference Burgos Gil, Philippon and SombraBPS14, Def 3.5.6]).
$\mathcal {X}$ is its canonical toric integral model (see [Reference MaillotMai00, § 2] and [Reference Burgos Gil, Philippon and SombraBPS14, Def 3.5.6]).
Theorem 1.2 Let ![]() $X\!$ be an
$X\!$ be an ![]() $n$-dimensional K-semistable toric Fano variety and denote by
$n$-dimensional K-semistable toric Fano variety and denote by ![]() $\mathcal {X}$ its canonical model over
$\mathcal {X}$ its canonical model over ![]() $\mathbb {Z}$. Then the previous conjecture holds under any one of the following conditions:
$\mathbb {Z}$. Then the previous conjecture holds under any one of the following conditions:
•
 $n\leq 6$ and
$n\leq 6$ and  $X\!$ is
$X\!$ is  $\mathbb {Q}$-factorial (equivalently,
$\mathbb {Q}$-factorial (equivalently,  $X\!$ is non-singular or has abelian quotient singularities);
$X\!$ is non-singular or has abelian quotient singularities);•
 $X\!$ is not Gorenstein or has some abelian quotient singularity.
$X\!$ is not Gorenstein or has some abelian quotient singularity.
Note that when ![]() $n=2$ any toric variety is, in fact,
$n=2$ any toric variety is, in fact, ![]() $\mathbb {Q}$-factorial. More generally, we will show that the curvature assumption may be dispensed with if the height
$\mathbb {Q}$-factorial. More generally, we will show that the curvature assumption may be dispensed with if the height ![]() $(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ is replaced by the
$(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ is replaced by the ![]() $\chi$-arithmetic volume
$\chi$-arithmetic volume ![]() $\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathcal {X}}})$ of
$\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathcal {X}}})$ of ![]() $\overline {-\mathcal {K}_{\mathcal {X}}}$ (whose definition is recalled in § 2.2.2). We expect that the maximum of
$\overline {-\mathcal {K}_{\mathcal {X}}}$ (whose definition is recalled in § 2.2.2). We expect that the maximum of ![]() $\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathcal {X}}})$ over all integral models
$\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathcal {X}}})$ over all integral models ![]() $(\mathcal {X},-\mathcal {K}_{\mathcal {X}})$ of a given toric Fano variety
$(\mathcal {X},-\mathcal {K}_{\mathcal {X}})$ of a given toric Fano variety ![]() $(X,-K_{X}\!)$ is attained at the canonical integral model
$(X,-K_{X}\!)$ is attained at the canonical integral model ![]() $\mathcal {X}$ featuring in the previous theorem. This expectation is inspired by a conjecture of Odaka discussed in § 1.4 below.
$\mathcal {X}$ featuring in the previous theorem. This expectation is inspired by a conjecture of Odaka discussed in § 1.4 below.
The key ingredient in the proof of Theorem 1.2 is the following bound estimating the arithmetic volume ![]() $\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathcal {X}}})$ of any volume-normalized metric on
$\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathcal {X}}})$ of any volume-normalized metric on ![]() $-K_{X\!}$ in terms of the algebro-geometric volume
$-K_{X\!}$ in terms of the algebro-geometric volume ![]() $\mathrm {vol}{(X)}$ (Proposition 3.7):
$\mathrm {vol}{(X)}$ (Proposition 3.7):
Since ![]() $\mathrm {vol}(X)$ is maximal for
$\mathrm {vol}(X)$ is maximal for ![]() $X=\mathbb {P}^{n}$ the right-hand side above is bounded by a constant
$X=\mathbb {P}^{n}$ the right-hand side above is bounded by a constant ![]() $C_{n}$ only depending on the dimension
$C_{n}$ only depending on the dimension ![]() $n$. Under the ‘gap hypothesis’ that
$n$. Under the ‘gap hypothesis’ that ![]() $\mathbb {P}^{n-1}\times \mathbb {P}^{1}$ has the second largest volume among all
$\mathbb {P}^{n-1}\times \mathbb {P}^{1}$ has the second largest volume among all ![]() $n$-dimensional K-semistable
$n$-dimensional K-semistable ![]() $X\!$, we show that the bound (1.4) implies Conjecture 1.1 for the canonical integral model
$X\!$, we show that the bound (1.4) implies Conjecture 1.1 for the canonical integral model ![]() $\mathcal {X}$ of a toric Fano variety
$\mathcal {X}$ of a toric Fano variety ![]() $X$. The proof of Theorem 1.2 is concluded by verifying the gap hypothesis under the conditions in Theorem 1.2. But we do expect that the gap hypothesis above holds for any toric Fano variety (see § 3.2.1).
$X$. The proof of Theorem 1.2 is concluded by verifying the gap hypothesis under the conditions in Theorem 1.2. But we do expect that the gap hypothesis above holds for any toric Fano variety (see § 3.2.1).
In a sequel [Reference Andreasson and BermanAB23] to the present paper Conjecture 1.1 is established for any diagonal Fano hypersurface ![]() $\mathcal {X}$ in
$\mathcal {X}$ in ![]() $\mathbb {P}_{\mathbb {Z}}^{n+1}$ (i.e.
$\mathbb {P}_{\mathbb {Z}}^{n+1}$ (i.e. ![]() $\mathcal {X}$ is the subscheme cut out by a homogeneous polynomial of the form
$\mathcal {X}$ is the subscheme cut out by a homogeneous polynomial of the form ![]() $a_{0}x_{0}^{d}+\cdots +a_{n+1}x_{n+1}^{d}$ for any given integers
$a_{0}x_{0}^{d}+\cdots +a_{n+1}x_{n+1}^{d}$ for any given integers ![]() $a_{i},$ with no common divisors, and
$a_{i},$ with no common divisors, and ![]() $d\leq n+1)$. Although
$d\leq n+1)$. Although ![]() $\mathcal {X}$ is not toric the proof, somewhat surprisingly, is reduced to a simple toric logarithmic case.
$\mathcal {X}$ is not toric the proof, somewhat surprisingly, is reduced to a simple toric logarithmic case.
1.2 The height of toric Kähler–Einstein metrics
In the toric case, ![]() $X\!$ is K-semistable if and only if it is K-polystable and thus admits a toric Kähler–Einstein metric [Reference Wang and ZhuWZ04, Reference Berman and BerndtssonBB13], i.e. a toric continuous metric on
$X\!$ is K-semistable if and only if it is K-polystable and thus admits a toric Kähler–Einstein metric [Reference Wang and ZhuWZ04, Reference Berman and BerndtssonBB13], i.e. a toric continuous metric on ![]() $-K_{X\!}$ whose curvature form defines a Kähler metric with constant positive Ricci curvature on the regular locus of
$-K_{X\!}$ whose curvature form defines a Kähler metric with constant positive Ricci curvature on the regular locus of ![]() $X$. Moreover, in general, any volume-normalized Kähler–Einstein metric maximizes
$X$. Moreover, in general, any volume-normalized Kähler–Einstein metric maximizes ![]() $(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$. This means that the inequality in the previous theorem is equivalent to the corresponding inequality for the volume-normalized toric Kähler–Einstein metric on
$(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$. This means that the inequality in the previous theorem is equivalent to the corresponding inequality for the volume-normalized toric Kähler–Einstein metric on ![]() $-K_{X}$. The special role of the Kähler–Einstein condition in arithmetic (Arakelov) geometry – as an analog of minimality of
$-K_{X}$. The special role of the Kähler–Einstein condition in arithmetic (Arakelov) geometry – as an analog of minimality of ![]() $\mathcal {X}$ over
$\mathcal {X}$ over ![]() $\mathrm {Spec} {\mathbb {Z}}$ – was emphasized in the early days of Arakelov geometry by Manin [Reference ManinMan85]. It is, however, rare that the Kähler–Einstein metric and the corresponding height, can be explicitly computed. In fact, in the Fano case this seems to only have been achieved when
$\mathrm {Spec} {\mathbb {Z}}$ – was emphasized in the early days of Arakelov geometry by Manin [Reference ManinMan85]. It is, however, rare that the Kähler–Einstein metric and the corresponding height, can be explicitly computed. In fact, in the Fano case this seems to only have been achieved when ![]() $X\!$ is homogeneous [Reference MaillotMai95, Reference Cassaigne and MaillotCM00, Reference Kaiser and KöhlerKK02, Reference TamvakisTam99a, Reference TamvakisTam99b, Reference TamvakisTam00]. The following result, complementing the general upper bound (1.4), yields a rather precise control on its height
$X\!$ is homogeneous [Reference MaillotMai95, Reference Cassaigne and MaillotCM00, Reference Kaiser and KöhlerKK02, Reference TamvakisTam99a, Reference TamvakisTam99b, Reference TamvakisTam00]. The following result, complementing the general upper bound (1.4), yields a rather precise control on its height ![]() $(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ in the toric case.
$(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ in the toric case.
Theorem 1.3 Let ![]() $X\!$ be an
$X\!$ be an ![]() $n$-dimensional toric Fano variety and denote by
$n$-dimensional toric Fano variety and denote by ![]() $\mathcal {X}$ its canonical model over
$\mathcal {X}$ its canonical model over ![]() $\mathbb {Z}$. Then the height
$\mathbb {Z}$. Then the height ![]() $(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ of any volume-normalized Kähler–Einstein metric satisfies
$(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ of any volume-normalized Kähler–Einstein metric satisfies
where ![]() $m_{n}$ denotes the largest lower bound on the Mahler volume of a convex body. In particular,
$m_{n}$ denotes the largest lower bound on the Mahler volume of a convex body. In particular, ![]() $(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}>0$.
$(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}>0$.
We also provide an infinite family of toric varieties ![]() $X\!$ for which the height of the corresponding Kähler–Einstein can be explicitly computed as a function
$X\!$ for which the height of the corresponding Kähler–Einstein can be explicitly computed as a function ![]() $f(v)$ of
$f(v)$ of ![]() $\mathrm {vol}(X)$ of the same form as in the previous theorem:
$\mathrm {vol}(X)$ of the same form as in the previous theorem: ![]() $f(v)=v\log (av^{-1})$ for some constant
$f(v)=v\log (av^{-1})$ for some constant ![]() $a$. The constant
$a$. The constant ![]() $m_{n}$ in the previous theorem is the largest constant satisfying
$m_{n}$ in the previous theorem is the largest constant satisfying
where ![]() $P^{*}$ denotes the polar dual of any given convex body
$P^{*}$ denotes the polar dual of any given convex body ![]() $P$ containing the origin in its interior (the role of
$P$ containing the origin in its interior (the role of ![]() $P$ in the present setting is played by the moment polytope of
$P$ in the present setting is played by the moment polytope of ![]() $X)$. According to Mahler's conjecture, the constant
$X)$. According to Mahler's conjecture, the constant ![]() $m_{n}$ is equal to
$m_{n}$ is equal to ![]() $(n+1)^{n+1}/(n!)^{2}$ (which is realized for a simplex
$(n+1)^{n+1}/(n!)^{2}$ (which is realized for a simplex ![]() $P$). The case
$P$). The case ![]() $n=2$ was settled in [Reference MahlerMah39], but for our purposes the following general bound from [Reference KuperbergKup08] will be enough:
$n=2$ was settled in [Reference MahlerMah39], but for our purposes the following general bound from [Reference KuperbergKup08] will be enough:
which implies the strict positivity of ![]() $(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$. Combining the previous theorem with the upper bound (1.1) thus yields the following universal bounds.
$(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$. Combining the previous theorem with the upper bound (1.1) thus yields the following universal bounds.
Corollary 1.4 Let ![]() $X\!$ be an
$X\!$ be an ![]() $n$-dimensional toric Fano variety and denote by
$n$-dimensional toric Fano variety and denote by ![]() $\mathcal {X}$ its canonical model over
$\mathcal {X}$ its canonical model over ![]() $\mathbb {Z}$. Then the height
$\mathbb {Z}$. Then the height ![]() $(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ of any volume-normalized Kähler–Einstein metric satisfies the following universal bounds:
$(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ of any volume-normalized Kähler–Einstein metric satisfies the following universal bounds:
Incidentally, the upper bound above is related to a question posed in [Reference Nakashima and TakedaNT96], asking whether ![]() $(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ is bounded from above by a universal constant
$(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ is bounded from above by a universal constant ![]() $C_{n},$ under the assumption that
$C_{n},$ under the assumption that ![]() $X\!$ be non-singular and
$X\!$ be non-singular and ![]() $\overline {-\mathcal {K}_{\mathcal {X}}}$ be relatively ample. This is a stronger condition than having positive curvature, as we assume. We also allow singularities, but our results concern only the toric case. Under the conditions in Theorem 1.2 our upper bound may be improved to the sharp bound
$\overline {-\mathcal {K}_{\mathcal {X}}}$ be relatively ample. This is a stronger condition than having positive curvature, as we assume. We also allow singularities, but our results concern only the toric case. Under the conditions in Theorem 1.2 our upper bound may be improved to the sharp bound ![]() $(\overline {-\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n}}})^{n+1}$ (given by formula (1.2)). As for the lower bound, it is sharp in any dimension
$(\overline {-\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n}}})^{n+1}$ (given by formula (1.2)). As for the lower bound, it is sharp in any dimension ![]() $n$. Indeed, there are
$n$. Indeed, there are ![]() $n$-dimensional K-semistable (
$n$-dimensional K-semistable (![]() $\mathbb {Q}$-factorial) Fano varieties
$\mathbb {Q}$-factorial) Fano varieties ![]() $X\!$ such that
$X\!$ such that ![]() $\mathrm {vol}(X)$ and thus (by Theorem 1.3)
$\mathrm {vol}(X)$ and thus (by Theorem 1.3) ![]() $(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ is arbitrarily close to
$(\overline {-\mathcal {K}_{\mathcal {X}}})^{n+1}$ is arbitrarily close to ![]() $0;$ see Example 3.1.
$0;$ see Example 3.1.
1.3 Donaldson's toric invariant
Let ![]() $(X,L)$ now be a polarized complex projective manifold. A prominent role in Kähler geometry is played by Mabuchi's K-energy functional
$(X,L)$ now be a polarized complex projective manifold. A prominent role in Kähler geometry is played by Mabuchi's K-energy functional ![]() $\mathcal {M}$ [Reference MabuchiMab86], defined on the space
$\mathcal {M}$ [Reference MabuchiMab86], defined on the space ![]() $\mathcal {H}(X,L)$ of all smooth metrics
$\mathcal {H}(X,L)$ of all smooth metrics ![]() $\Vert \cdot \Vert$ on
$\Vert \cdot \Vert$ on ![]() $L$ with positive curvature. Its critical points are the metrics whose curvature form
$L$ with positive curvature. Its critical points are the metrics whose curvature form ![]() $\omega$ defines a Kähler metric on
$\omega$ defines a Kähler metric on ![]() $X\!$ with constant scalar curvature. The precise definition of
$X\!$ with constant scalar curvature. The precise definition of ![]() $\mathcal {M}$ is recalled in § 4.1. Since the definition of
$\mathcal {M}$ is recalled in § 4.1. Since the definition of ![]() $\mathcal {M}$ only involves its differential, the functional
$\mathcal {M}$ only involves its differential, the functional ![]() $\mathcal {M}$ is only defined up to addition by a real constant. However, when
$\mathcal {M}$ is only defined up to addition by a real constant. However, when ![]() $(X,L)$ is toric, Donaldson [Reference DonaldsonDon02] exploited the toric structure to define the Mabuchi functional
$(X,L)$ is toric, Donaldson [Reference DonaldsonDon02] exploited the toric structure to define the Mabuchi functional ![]() $\mathcal {M}$ as a canonical functional on toric metrics:
$\mathcal {M}$ as a canonical functional on toric metrics:
where ![]() $P$ is the moment polytope in
$P$ is the moment polytope in ![]() $\mathbb {R}^{n}$ corresponding to the polarized toric manifold
$\mathbb {R}^{n}$ corresponding to the polarized toric manifold ![]() $(X,L),$ whose boundary
$(X,L),$ whose boundary ![]() $\partial P$ comes with a measure
$\partial P$ comes with a measure ![]() $d\sigma$ induced by Lebesgue measure
$d\sigma$ induced by Lebesgue measure ![]() $dx$ on
$dx$ on ![]() $\mathbb {R}^{n}$ and the lattice
$\mathbb {R}^{n}$ and the lattice ![]() $\mathbb {Z}^{n}$ in
$\mathbb {Z}^{n}$ in ![]() $\mathbb {R}^{n}$ and
$\mathbb {R}^{n}$ and ![]() $u$ is the smooth bounded convex function on
$u$ is the smooth bounded convex function on ![]() $P$ corresponding to a toric metric on
$P$ corresponding to a toric metric on ![]() $L$ under Legendre transformation (see § 3.1.2). In particular, in the last section of [Reference DonaldsonDon02] Donaldson introduced an invariant of a polarized toric manifold
$L$ under Legendre transformation (see § 3.1.2). In particular, in the last section of [Reference DonaldsonDon02] Donaldson introduced an invariant of a polarized toric manifold ![]() $(X,L),$ defined as the infimum of the toric Mabuchi functional
$(X,L),$ defined as the infimum of the toric Mabuchi functional ![]() $\mathcal {M}_{L}$ defined by formula (1.5). Here we show that Theorem 1.2 implies that when
$\mathcal {M}_{L}$ defined by formula (1.5). Here we show that Theorem 1.2 implies that when ![]() $X\!$ is a Fano variety and
$X\!$ is a Fano variety and ![]() $L=-K_{X\!}$, a slight perturbation of Donaldson's invariant is minimal when
$L=-K_{X\!}$, a slight perturbation of Donaldson's invariant is minimal when ![]() $X\!$ is complex projective space, under the conditions on
$X\!$ is complex projective space, under the conditions on ![]() $X\!$ appearing in Theorem 1.2.
$X\!$ appearing in Theorem 1.2.
Theorem 1.5 Let ![]() $X\!$ be a K-semistable toric Fano variety of dimension
$X\!$ be a K-semistable toric Fano variety of dimension ![]() $n,$ satisfying the conditions in Theorem 1.2. Then the invariant
$n,$ satisfying the conditions in Theorem 1.2. Then the invariant
is minimal for ![]() $X=\mathbb {P}^{n}$ (and only then), where the infimum is attained at the metric on
$X=\mathbb {P}^{n}$ (and only then), where the infimum is attained at the metric on ![]() $-K_{\mathbb {P}^{n}}$ induced by the Fubini–Study metric.
$-K_{\mathbb {P}^{n}}$ induced by the Fubini–Study metric.
In the previous theorem the Fano variety ![]() $X\!$ is allowed to be singular. The Mabuchi functional for singular general Fano varieties was introduced in [Reference Ding and TianDT92, Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19], and Donaldson's formula (1.5) was extended to singular toric Fano varieties in [Reference Berman and BerndtssonBB13]. In general, for Fano varieties the Mabuchi functional
$X\!$ is allowed to be singular. The Mabuchi functional for singular general Fano varieties was introduced in [Reference Ding and TianDT92, Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19], and Donaldson's formula (1.5) was extended to singular toric Fano varieties in [Reference Berman and BerndtssonBB13]. In general, for Fano varieties the Mabuchi functional ![]() $\mathcal {M}$ is bounded from below if and only if
$\mathcal {M}$ is bounded from below if and only if ![]() $X\!$ is K-semistable [Reference LiLi17] (see the discussion following Theorem 2.5).
$X\!$ is K-semistable [Reference LiLi17] (see the discussion following Theorem 2.5).
1.4 The arithmetic Mabuchi functional and Odaka's modular height
For a general polarized manifold ![]() $(X,L)$ the infimum of the Mabuchi functional
$(X,L)$ the infimum of the Mabuchi functional ![]() $\mathcal {M}$ is not canonically defined (since
$\mathcal {M}$ is not canonically defined (since ![]() $\mathcal {M}$ is only defined up to addition by a constant). But to any given integral model
$\mathcal {M}$ is only defined up to addition by a constant). But to any given integral model ![]() $(\mathcal {X},\mathcal {L})$ of a polarized complex variety
$(\mathcal {X},\mathcal {L})$ of a polarized complex variety ![]() $(X,L)$ one may, as shown by Odaka [Reference OdakaOda18], attach a particular Mabuchi functional
$(X,L)$ one may, as shown by Odaka [Reference OdakaOda18], attach a particular Mabuchi functional ![]() $\mathcal {M}_{(\mathcal {X},\mathcal {L})}$ which (up to a multiplicative normalization) is given as the following sum of arithmetic intersection numbers:
$\mathcal {M}_{(\mathcal {X},\mathcal {L})}$ which (up to a multiplicative normalization) is given as the following sum of arithmetic intersection numbers:
where, as in the previous section, ![]() $\overline {\mathcal {L}}$ denotes the metrized line bundle
$\overline {\mathcal {L}}$ denotes the metrized line bundle ![]() $(\mathcal {L}, \Vert \cdot \Vert )$. In the definition of the second arithmetic intersection number above one also needs to endow
$(\mathcal {L}, \Vert \cdot \Vert )$. In the definition of the second arithmetic intersection number above one also needs to endow ![]() $-K_{X\!}$ with a metric and one is confronted with two different natural choices: either the metric induced by the volume form
$-K_{X\!}$ with a metric and one is confronted with two different natural choices: either the metric induced by the volume form ![]() $\omega ^{n}/n!$ of the Kähler metric
$\omega ^{n}/n!$ of the Kähler metric ![]() $\omega$ defined by the curvature form of
$\omega$ defined by the curvature form of ![]() $(\mathcal {L},\Vert \cdot \Vert )$ or the normalized volume form
$(\mathcal {L},\Vert \cdot \Vert )$ or the normalized volume form ![]() $\omega ^{n}/L^{n}$ (which has unit total volume). The first choice is the one adopted in [Reference OdakaOda18], and we show that when
$\omega ^{n}/L^{n}$ (which has unit total volume). The first choice is the one adopted in [Reference OdakaOda18], and we show that when ![]() $X\!$ is a toric Fano variety and
$X\!$ is a toric Fano variety and ![]() $(\mathcal {X},\mathcal {L})$ is the canonical integral model of (
$(\mathcal {X},\mathcal {L})$ is the canonical integral model of (![]() $X,L)$ this choice coincides with Donaldson's one (formula (1.5)). However, for our purposes the second volume-normalized choice turns out to be the appropriate one. It yields, in particular, the shift by the logarithm of
$X,L)$ this choice coincides with Donaldson's one (formula (1.5)). However, for our purposes the second volume-normalized choice turns out to be the appropriate one. It yields, in particular, the shift by the logarithm of ![]() $(-K_{X}\!)^{n}$ appearing in Theorem 1.5:
$(-K_{X}\!)^{n}$ appearing in Theorem 1.5:
(Proposition 5.2). The point is that with this choice the following formula holds in the arithmetic setting:
 \begin{equation} \sup\frac{\bigl(\overline{-\mathcal{K}_{\mathcal{X}}}\bigr)^{n+1}}{(n+1)!}=-\inf_{\mathcal{H}(X,-K_{X})}\mathcal{M}_{(\mathcal{X},-\mathcal{K}_{\mathcal{X}})}, \end{equation}
\begin{equation} \sup\frac{\bigl(\overline{-\mathcal{K}_{\mathcal{X}}}\bigr)^{n+1}}{(n+1)!}=-\inf_{\mathcal{H}(X,-K_{X})}\mathcal{M}_{(\mathcal{X},-\mathcal{K}_{\mathcal{X}})}, \end{equation}
where the supremum ranges over all volume-normalized metrics in ![]() $\mathcal {H}(X,-K_{X}\!)$ (see Proposition 5.3). As a consequence, Conjecture 1.1 is equivalent to the inequality
$\mathcal {H}(X,-K_{X}\!)$ (see Proposition 5.3). As a consequence, Conjecture 1.1 is equivalent to the inequality
Theorem 1.5 thus follows from Theorem 1.2.
1.4.1 Odaka's modular height
Let ![]() $(X_{F},L_{F})$ be an
$(X_{F},L_{F})$ be an ![]() $n$-dimensional polarized variety defined over a number field
$n$-dimensional polarized variety defined over a number field ![]() $F$. In [Reference OdakaOda18] Odaka introduced the following invariant of
$F$. In [Reference OdakaOda18] Odaka introduced the following invariant of ![]() $(X_{F},L_{F}),$ dubbed the intrinsic K-modular height of
$(X_{F},L_{F}),$ dubbed the intrinsic K-modular height of ![]() $(X_{F},L_{F})$:
$(X_{F},L_{F})$:
where ![]() $(\mathcal {X},\mathcal {L})$ is a model of
$(\mathcal {X},\mathcal {L})$ is a model of ![]() $(X_{F},L_{F})$ over the rings of integers
$(X_{F},L_{F})$ over the rings of integers ![]() $\mathcal {O}_{F'}$ of a finite field extension
$\mathcal {O}_{F'}$ of a finite field extension ![]() $F'$ of
$F'$ of ![]() $F$ and
$F$ and ![]() $\mathcal {M}_{(\mathcal {X},\mathcal {L})}$ now denotes the arithmetic K-energy (1.6), divided by the degree
$\mathcal {M}_{(\mathcal {X},\mathcal {L})}$ now denotes the arithmetic K-energy (1.6), divided by the degree ![]() $[F':\mathbb {Q}]$. In contrast to [Reference OdakaOda18], we will employ the volume-normalized metric on
$[F':\mathbb {Q}]$. In contrast to [Reference OdakaOda18], we will employ the volume-normalized metric on ![]() $-K_{X\!}$ in the definition of
$-K_{X\!}$ in the definition of ![]() $\mathcal {M}_{(\mathcal {X},\mathcal {L})},$ discussed in the previous section. As shown in (1.6), for a polarized abelian variety
$\mathcal {M}_{(\mathcal {X},\mathcal {L})},$ discussed in the previous section. As shown in (1.6), for a polarized abelian variety ![]() $(X_{F},L_{F})$, Odaka's modular height
$(X_{F},L_{F})$, Odaka's modular height ![]() $h(X_{F},L_{F})$ essentially coincides with Faltings’s stable modular height of
$h(X_{F},L_{F})$ essentially coincides with Faltings’s stable modular height of ![]() $(X_{K},L_{K})$ [Reference FaltingsFal83a] (see § 6.4). Furthermore, as explained in [Reference OdakaOda18],
$(X_{K},L_{K})$ [Reference FaltingsFal83a] (see § 6.4). Furthermore, as explained in [Reference OdakaOda18], ![]() $h(X_{F},L_{F})$ can be viewed as a ‘large rank limit’ of Bost and Zhang's intrinsic heights appearing in [Reference BostBos94, Reference BostBos96, Reference ZhangZha96], where the role of K-semistability is played by Chow semistability (see formula (6.8)). We propose the following conjecture.
$h(X_{F},L_{F})$ can be viewed as a ‘large rank limit’ of Bost and Zhang's intrinsic heights appearing in [Reference BostBos94, Reference BostBos96, Reference ZhangZha96], where the role of K-semistability is played by Chow semistability (see formula (6.8)). We propose the following conjecture.
Conjecture 1.6 Let ![]() $X_{\mathbb {Q}}$ be a Fano variety defined over
$X_{\mathbb {Q}}$ be a Fano variety defined over ![]() $\mathbb {Q}$. Then Odaka's modular invariant
$\mathbb {Q}$. Then Odaka's modular invariant ![]() $h(X_{\mathbb {Q}},-K_{X_{\mathbb {Q}}}),$ normalized as above, is minimal when
$h(X_{\mathbb {Q}},-K_{X_{\mathbb {Q}}}),$ normalized as above, is minimal when ![]() $X_{\mathbb {Q}}=\mathbb {P}_{\mathbb {Q}}^{n}$.
$X_{\mathbb {Q}}=\mathbb {P}_{\mathbb {Q}}^{n}$.
According to a conjecture of Odaka [Reference OdakaOda20], any globally K-semistable integral model ![]() $(\mathcal {X},-\mathcal {K}_{\mathcal {X}})$ of
$(\mathcal {X},-\mathcal {K}_{\mathcal {X}})$ of ![]() $(X,-K_{X}\!)$ minimizes
$(X,-K_{X}\!)$ minimizes ![]() $\mathcal {M}_{(\mathcal {X},\mathcal {L})}$ over all models
$\mathcal {M}_{(\mathcal {X},\mathcal {L})}$ over all models ![]() $(\mathcal {X},\mathcal {L})$ (the function field analog of this minimization property is established in [Reference Blum and XuBX19]; see also [Reference XuXu21, Remark 7.9]). Global K-semistability means that all the fibers of
$(\mathcal {X},\mathcal {L})$ (the function field analog of this minimization property is established in [Reference Blum and XuBX19]; see also [Reference XuXu21, Remark 7.9]). Global K-semistability means that all the fibers of ![]() $\mathcal {X}\rightarrow \mathrm {Spec} {\mathcal {O}_{F}}$ are K-semistable. In other words, in addition to the K-semistability of the generic fiber
$\mathcal {X}\rightarrow \mathrm {Spec} {\mathcal {O}_{F}}$ are K-semistable. In other words, in addition to the K-semistability of the generic fiber ![]() $X_{F}$, this means that the variety
$X_{F}$, this means that the variety ![]() $X_{\mathbb {F}_{p}}$ over the finite field
$X_{\mathbb {F}_{p}}$ over the finite field ![]() $\mathbb {F}_{p},$ corresponding to the integral model
$\mathbb {F}_{p},$ corresponding to the integral model ![]() $\mathcal {X},$ is K-semistable for any prime ideal
$\mathcal {X},$ is K-semistable for any prime ideal ![]() $p$. For example, as pointed out to us by Odaka, the canonical model
$p$. For example, as pointed out to us by Odaka, the canonical model ![]() $\mathcal {X}$ of a K-semistable toric Fano variety
$\mathcal {X}$ of a K-semistable toric Fano variety ![]() $X_{\mathbb {Q}}$ appearing in Theorem 1.2 is globally K-semistable. Thus if Odaka's minimization conjecture holds, then Theorem 1.2 implies Conjecture 1.6 for any toric Fano variety
$X_{\mathbb {Q}}$ appearing in Theorem 1.2 is globally K-semistable. Thus if Odaka's minimization conjecture holds, then Theorem 1.2 implies Conjecture 1.6 for any toric Fano variety ![]() $X_{\mathbb {Q}}$ satisfying the conditions in Theorem 1.2.Footnote 1 In any case, the positivity statement in Theorem 1.3 implies that the modular invariant
$X_{\mathbb {Q}}$ satisfying the conditions in Theorem 1.2.Footnote 1 In any case, the positivity statement in Theorem 1.3 implies that the modular invariant ![]() $h(X_{\mathbb {Q}},-K_{X_{\mathbb {Q}}})$ is negative for any K-semistable toric Fano variety
$h(X_{\mathbb {Q}},-K_{X_{\mathbb {Q}}})$ is negative for any K-semistable toric Fano variety ![]() $X_{\mathbb {Q}}$.
$X_{\mathbb {Q}}$.
1.5 Organization
In § 2 we start by recalling the complex geometric and arithmetic setup before proving Theorem 2.5, relating upper bounds on the height of Fano varieties to K-semistability. The proof leverages an arithmetic analog of the Ding functional. In § 3 we specialize to the toric situation and prove the sharp height inequality in Theorem 1.2 and the height bounds for Kähler–Einstein metrics in Theorem 1.3. We also show that Conjecture 1.1 is compatible with taking products. We then go on, in § 4, to deduce Theorem 1.5 concerning the sharp lower bound on Donaldson's toric Mabuchi functional. In § 5 Donaldson's functional is related to Odaka's arithmetic Mabuchi functional, which in turn is related to the arithmetic Ding functional. In the last section we make a comparison with the function field case, formulate a generalized version of Conjecture 1.1 and compare with previous work of Bost and Zhang, Odaka and Faltings.
We have made an effort to make the paper readable for the reader with a background in arithmetic geometry, as well as for complex geometers, by including most of the background material needed for the proofs of the main results.
2. Heights, arithmetic volumes and K-stability of Fano varieties
In this section we show, in particular, that the height of a polarized integral model ![]() $(\mathcal {X},\mathcal {L})$ of a Fano manifold
$(\mathcal {X},\mathcal {L})$ of a Fano manifold ![]() $(X,-K_{X}\!)$ is bounded from above – as the metric on
$(X,-K_{X}\!)$ is bounded from above – as the metric on ![]() $\mathcal {L}$ ranges over all volume-normalized metrics with positive curvature current – if and only if
$\mathcal {L}$ ranges over all volume-normalized metrics with positive curvature current – if and only if ![]() $(X,-K_{X}\!)$ is K-semistable (Theorem 2.5). See also [Reference OdakaOda18] for further connections between K-stability of polarized varieties
$(X,-K_{X}\!)$ is K-semistable (Theorem 2.5). See also [Reference OdakaOda18] for further connections between K-stability of polarized varieties ![]() $(X,L)$ and arithmetic geometry. The main new feature here, compared to [Reference OdakaOda18], is that we leverage an arithmetic version of the Ding functional in Kähler geometry, while [Reference OdakaOda18] considers an arithmetic version of the Mabuchi functional (the two functionals are compared in § 5).
$(X,L)$ and arithmetic geometry. The main new feature here, compared to [Reference OdakaOda18], is that we leverage an arithmetic version of the Ding functional in Kähler geometry, while [Reference OdakaOda18] considers an arithmetic version of the Mabuchi functional (the two functionals are compared in § 5).
2.1 Complex geometric setup
Throughout the paper ![]() $X\!$ will denote a compact connected complex normal variety, assumed to be
$X\!$ will denote a compact connected complex normal variety, assumed to be ![]() $\mathbb {Q}$-Gorenstein. This means that the canonical divisor
$\mathbb {Q}$-Gorenstein. This means that the canonical divisor ![]() $K_{X\!}$ on
$K_{X\!}$ on ![]() $X\!$ is defined as a
$X\!$ is defined as a ![]() $\mathbb {Q}$-line bundle: there exist some positive integer
$\mathbb {Q}$-line bundle: there exist some positive integer ![]() $m$ and a line bundle on
$m$ and a line bundle on ![]() $X\!$ whose restriction to the regular locus
$X\!$ whose restriction to the regular locus ![]() $X_{\mathrm {reg}}$ of
$X_{\mathrm {reg}}$ of ![]() $X\!$ coincides with the
$X\!$ coincides with the ![]() $m$th tensor power of
$m$th tensor power of ![]() $K_{X_{\mathrm {reg}}}$, i.e. the top exterior power of the cotangent bundle of
$K_{X_{\mathrm {reg}}}$, i.e. the top exterior power of the cotangent bundle of ![]() $X_{\mathrm {reg}}$. We will use additive notation for tensor powers of line bundles.
$X_{\mathrm {reg}}$. We will use additive notation for tensor powers of line bundles.
2.1.1 Metrics on line bundles
Let ![]() $(X,L)$ be a polarized complex projective variety, i.e. a complex normal variety
$(X,L)$ be a polarized complex projective variety, i.e. a complex normal variety ![]() $X\!$ endowed with an ample line bundle
$X\!$ endowed with an ample line bundle ![]() $L$. We will use additive notation for metrics on
$L$. We will use additive notation for metrics on ![]() $L$. This means that we identify a continuous Hermitian metric
$L$. This means that we identify a continuous Hermitian metric ![]() $\Vert \cdot \Vert$ on
$\Vert \cdot \Vert$ on ![]() $L$ with a collection of continuous local functions
$L$ with a collection of continuous local functions ![]() $\phi _{U}$ associated to a given covering of
$\phi _{U}$ associated to a given covering of ![]() $X\!$ by open subsets
$X\!$ by open subsets ![]() $U$ and trivializing holomorphic sections
$U$ and trivializing holomorphic sections ![]() $e_{U}$ of
$e_{U}$ of ![]() $L\rightarrow U$:
$L\rightarrow U$:
which defines a function on ![]() $U$. Of course, the functions
$U$. Of course, the functions ![]() $\phi _{U}$ on
$\phi _{U}$ on ![]() $U$ do not glue to define a global function on
$U$ do not glue to define a global function on ![]() $X,$ but the current
$X,$ but the current
is globally well defined and coincides with the normalized curvature current of ![]() $\Vert \cdot \Vert$ (the normalization ensures that the corresponding cohomology class represents the first Chern class
$\Vert \cdot \Vert$ (the normalization ensures that the corresponding cohomology class represents the first Chern class ![]() $c_{1}(L)$ of
$c_{1}(L)$ of ![]() $L$ in the integral lattice of
$L$ in the integral lattice of ![]() $H^{2}(X,\mathbb {R}))$. Accordingly, as is customary, we will symbolically denote by
$H^{2}(X,\mathbb {R}))$. Accordingly, as is customary, we will symbolically denote by ![]() $\phi$ a given continuous Hermitian metric on
$\phi$ a given continuous Hermitian metric on ![]() $L$ and by
$L$ and by ![]() $dd^{c}\phi$ its curvature current. The space of all continuous metrics
$dd^{c}\phi$ its curvature current. The space of all continuous metrics ![]() $\phi$ on
$\phi$ on ![]() $L$ will be denoted by
$L$ will be denoted by ![]() $\mathcal {C}^{0}(L)$. We will denote by
$\mathcal {C}^{0}(L)$. We will denote by ![]() $\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$ the space of all continuous metrics on
$\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$ the space of all continuous metrics on ![]() $L$ whose curvature current is positive,
$L$ whose curvature current is positive, ![]() $dd^{c}\phi \geq 0$ (which means that
$dd^{c}\phi \geq 0$ (which means that ![]() $\phi _{U}$ is plurisubharmonic (psh)). Then the exterior powers of
$\phi _{U}$ is plurisubharmonic (psh)). Then the exterior powers of ![]() $dd^{c}\phi$ are defined using the local pluripotential theory of Bedford and Taylor [Reference Berman and BoucksomBB10]. The volume of an ample line bundle
$dd^{c}\phi$ are defined using the local pluripotential theory of Bedford and Taylor [Reference Berman and BoucksomBB10]. The volume of an ample line bundle ![]() $L$ may be defined by
$L$ may be defined by
using in the second equality the Hilbert–Samuel theorem and where ![]() $\phi$ denotes any element in
$\phi$ denotes any element in ![]() $\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$.
$\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$.
More generally, metrics ![]() $\phi$ are defined for a
$\phi$ are defined for a ![]() $\mathbb {Q}$-line bundle
$\mathbb {Q}$-line bundle ![]() $L$: if
$L$: if ![]() $mL$ is a bona fide line bundle, for
$mL$ is a bona fide line bundle, for ![]() $m\in \mathbb {Z}_{+},$ then
$m\in \mathbb {Z}_{+},$ then ![]() $m\phi$ is a bona fide metric on
$m\phi$ is a bona fide metric on ![]() $mL$.
$mL$.
Remark 2.1 The normalization of ![]() $\phi _{U}$ used here coincides with the one in [Reference BermanBer16, Reference Berman and BerndtssonBB13], but it is twice the one employed in [Reference Berman and BoucksomBB10].
$\phi _{U}$ used here coincides with the one in [Reference BermanBer16, Reference Berman and BerndtssonBB13], but it is twice the one employed in [Reference Berman and BoucksomBB10].
2.1.2 Metrics on  $-K_{X\!}$ versus volume forms on
$-K_{X\!}$ versus volume forms on  $X$
$X$
First consider the case when ![]() $X\!$ is smooth. Then any smooth metric
$X\!$ is smooth. Then any smooth metric ![]() $\Vert \cdot \Vert$ on
$\Vert \cdot \Vert$ on ![]() $-K_{X\!}$ corresponds to a volume form on
$-K_{X\!}$ corresponds to a volume form on ![]() $X,$ defined as follows. Given local holomorphic coordinates
$X,$ defined as follows. Given local holomorphic coordinates ![]() $z$ on
$z$ on ![]() $U\subset X$, denote by
$U\subset X$, denote by ![]() $e_{U}$ the corresponding trivialization of
$e_{U}$ the corresponding trivialization of ![]() $-K_{X},$ i.e.
$-K_{X},$ i.e. ![]() $e_{U}=\partial /\partial z_{1}\wedge \cdots \wedge \partial /\partial z_{n}$. The metric on
$e_{U}=\partial /\partial z_{1}\wedge \cdots \wedge \partial /\partial z_{n}$. The metric on ![]() $-K_{X\!}$ induces, as in § 2.1.1, a function
$-K_{X\!}$ induces, as in § 2.1.1, a function ![]() $\phi _{U}$ on
$\phi _{U}$ on ![]() $U$, and the volume form in question is locally defined by
$U$, and the volume form in question is locally defined by
 \begin{equation} e^{-\phi_{U}}\left(\frac{i}{2}\right)^{n^{2}}\,dz\wedge d\bar{z},\quad dz:=dz_{1}\wedge\cdots\wedge dz_{n}\end{equation}
\begin{equation} e^{-\phi_{U}}\left(\frac{i}{2}\right)^{n^{2}}\,dz\wedge d\bar{z},\quad dz:=dz_{1}\wedge\cdots\wedge dz_{n}\end{equation}
on ![]() $U,$ which glues to define a global volume form on
$U,$ which glues to define a global volume form on ![]() $X$. In other words,
$X$. In other words, ![]() $e^{-\phi _{U}}$ is the density of the volume form with respect to the local Euclidean volume form. Accordingly, we will simply denote the volume form in question by
$e^{-\phi _{U}}$ is the density of the volume form with respect to the local Euclidean volume form. Accordingly, we will simply denote the volume form in question by ![]() $e^{-\phi }$, abusing notation slightly. When
$e^{-\phi }$, abusing notation slightly. When ![]() $X\!$ is singular any continuous metric
$X\!$ is singular any continuous metric ![]() $\phi$ on
$\phi$ on ![]() $-K_{X\!}$ induces a measure on
$-K_{X\!}$ induces a measure on ![]() $X,$ symbolically denoted by
$X,$ symbolically denoted by ![]() $e^{-\phi },$ defined as before on the regular locus
$e^{-\phi },$ defined as before on the regular locus ![]() $X_{\mathrm {reg}}$ of
$X_{\mathrm {reg}}$ of ![]() $X\!$ and then extended by zero to all of
$X\!$ and then extended by zero to all of ![]() $X$. We will say that a measure
$X$. We will say that a measure ![]() $dV$ on
$dV$ on ![]() $X\!$ is a continuous volume form if it corresponds to a continuous metric on
$X\!$ is a continuous volume form if it corresponds to a continuous metric on ![]() $-K_{X}$. A Fano variety has log terminal singularities if and only if it admits a continuous volume form
$-K_{X}$. A Fano variety has log terminal singularities if and only if it admits a continuous volume form ![]() $dV$ with finite total volume [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19, § 3.1].
$dV$ with finite total volume [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19, § 3.1].
2.1.3 K-semistability
We briefly recall the notion of K-semistability (see [Reference DonaldsonDon02, Reference Ross and ThomasRT07, Reference WangWan12, Reference OdakaOda13a] for more background). A polarized complex projective variety ![]() $(X,L)$ is said to be K-semistable if the Donaldson–Futaki invariant
$(X,L)$ is said to be K-semistable if the Donaldson–Futaki invariant ![]() $\mathrm {DF}(\mathscr {X},\mathscr {L})$ of any test configuration
$\mathrm {DF}(\mathscr {X},\mathscr {L})$ of any test configuration ![]() $(\mathscr {X},\mathscr {L})$ for
$(\mathscr {X},\mathscr {L})$ for ![]() $(X,L)$ is non-negative. A test configuration
$(X,L)$ is non-negative. A test configuration ![]() $(\mathscr {X},\mathscr {L})$ is defined as a
$(\mathscr {X},\mathscr {L})$ is defined as a ![]() $\mathbb {C}^{*}$-equivariant normal model for
$\mathbb {C}^{*}$-equivariant normal model for ![]() $(X,L)$ over the complex affine line
$(X,L)$ over the complex affine line ![]() $\mathbb {C}$. More precisely,
$\mathbb {C}$. More precisely, ![]() $\mathscr {X\!}$ is a normal complex variety endowed with a
$\mathscr {X\!}$ is a normal complex variety endowed with a ![]() $\mathbb {C}^{*}$-action
$\mathbb {C}^{*}$-action ![]() $\rho$, a
$\rho$, a ![]() $\mathbb {C}^{*}$-equivariant holomorphic projection
$\mathbb {C}^{*}$-equivariant holomorphic projection ![]() $\pi$ to
$\pi$ to ![]() $\mathbb {C}$ and a relatively ample
$\mathbb {C}$ and a relatively ample ![]() $\mathbb {C}^{*}$-equivariant
$\mathbb {C}^{*}$-equivariant ![]() $\mathbb {Q}$-line bundle
$\mathbb {Q}$-line bundle ![]() $\mathscr {L}$ (endowed with a lift of
$\mathscr {L}$ (endowed with a lift of ![]() $\rho )$:
$\rho )$:
such that the fiber of ![]() $\mathscr {X\!}$ over
$\mathscr {X\!}$ over ![]() $1\in \mathbb {C}$ is equal to
$1\in \mathbb {C}$ is equal to ![]() $(X,L)$. Its Donaldson–Futaki invariant
$(X,L)$. Its Donaldson–Futaki invariant ![]() $\mathrm {DF}(\mathscr {X},\mathscr {L})\in \mathbb {R}$ may be defined as a normalized limit, as
$\mathrm {DF}(\mathscr {X},\mathscr {L})\in \mathbb {R}$ may be defined as a normalized limit, as ![]() $k\rightarrow \infty,$ of Chow weights of a sequence of one-parameter subgroups of
$k\rightarrow \infty,$ of Chow weights of a sequence of one-parameter subgroups of ![]() $GL(H^{0}(X,kL))$ induced by
$GL(H^{0}(X,kL))$ induced by ![]() $(\mathscr {X},\mathscr {L})$ (in the sense of geometric invariant theory). As a consequence,
$(\mathscr {X},\mathscr {L})$ (in the sense of geometric invariant theory). As a consequence, ![]() $(X,L)$ is K-semistable if, for example,
$(X,L)$ is K-semistable if, for example, ![]() $(X,kL)$ is Chow semistable, for
$(X,kL)$ is Chow semistable, for ![]() $k$ sufficiently large [Reference Ross and ThomasRT07]. However, for the purpose of the present paper it will be more convenient to employ the intersection-theoretic formula for
$k$ sufficiently large [Reference Ross and ThomasRT07]. However, for the purpose of the present paper it will be more convenient to employ the intersection-theoretic formula for ![]() $\mathrm {DF}(\mathscr {X},\mathscr {L})$ established in [Reference WangWan12, Reference OdakaOda13a]:
$\mathrm {DF}(\mathscr {X},\mathscr {L})$ established in [Reference WangWan12, Reference OdakaOda13a]:
where ![]() $\overline {\mathscr {L}}$ denotes the
$\overline {\mathscr {L}}$ denotes the ![]() $\mathbb {C}^{*}$-equivariant extension of
$\mathbb {C}^{*}$-equivariant extension of ![]() $\mathscr {L}$ to the
$\mathscr {L}$ to the ![]() $\mathbb {C}^{*}$-equivariant compactification
$\mathbb {C}^{*}$-equivariant compactification ![]() $\mathscr {\overline {X}}$ of
$\mathscr {\overline {X}}$ of ![]() $\mathscr {X\!}$ over
$\mathscr {X\!}$ over ![]() $\mathbb {P}^{1}$ and
$\mathbb {P}^{1}$ and ![]() $\mathscr {K}_{\mathcal {\mathscr {\overline {X}}}/\mathbb {P}^{1}}$ denotes the relative canonical divisor.
$\mathscr {K}_{\mathcal {\mathscr {\overline {X}}}/\mathbb {P}^{1}}$ denotes the relative canonical divisor.
Remark 2.2 Usually the definition of ![]() $\mathrm {DF}(\mathscr {X},\mathscr {L})$ involves a factor of
$\mathrm {DF}(\mathscr {X},\mathscr {L})$ involves a factor of ![]() $1/L^{n},$ but the present definition will be more convenient here (since the factor
$1/L^{n},$ but the present definition will be more convenient here (since the factor ![]() $L^{n}$ is positive it does not alter the definition of K-stability). It is made so that
$L^{n}$ is positive it does not alter the definition of K-stability). It is made so that ![]() $-(n+1)!\mathrm {DF}(\mathscr {X},\mathscr {L})=\overline {\mathscr {L}}^{n+1}$ when
$-(n+1)!\mathrm {DF}(\mathscr {X},\mathscr {L})=\overline {\mathscr {L}}^{n+1}$ when ![]() $\mathscr {L}=-\mathscr {K}_{\mathcal {\mathscr {\overline {X}}}/\mathbb {P}^{1}}$.
$\mathscr {L}=-\mathscr {K}_{\mathcal {\mathscr {\overline {X}}}/\mathbb {P}^{1}}$.
2.2 Arithmetic setup
Let ![]() $\mathcal {X}$ be a projective flat scheme
$\mathcal {X}$ be a projective flat scheme ![]() $\mathcal {X}\rightarrow \mathrm {Spec}{\mathbb {Z}}$ of relative dimension
$\mathcal {X}\rightarrow \mathrm {Spec}{\mathbb {Z}}$ of relative dimension ![]() $n,$ with the property that
$n,$ with the property that ![]() $\mathcal {X}$ is reduced and satisfies Serre's conditions
$\mathcal {X}$ is reduced and satisfies Serre's conditions ![]() $S_{2}$ (this is, for example, the case if
$S_{2}$ (this is, for example, the case if ![]() $\mathcal {X}$ is normal). Denote by
$\mathcal {X}$ is normal). Denote by ![]() $X\!$ the complex points of
$X\!$ the complex points of ![]() $\mathcal {X}$ and assume that
$\mathcal {X}$ and assume that ![]() $X\!$ is a normal projective variety over
$X\!$ is a normal projective variety over ![]() $\mathbb {C}$. Such a scheme
$\mathbb {C}$. Such a scheme ![]() $\mathcal {X}$ will be called an arithmetic variety. A polarized arithmetic variety
$\mathcal {X}$ will be called an arithmetic variety. A polarized arithmetic variety ![]() $(\mathcal {X},\mathcal {L}$) is an arithmetic variety endowed with a relatively ample
$(\mathcal {X},\mathcal {L}$) is an arithmetic variety endowed with a relatively ample ![]() $\mathbb {Q}$-line bundle
$\mathbb {Q}$-line bundle ![]() $\mathcal {L}$. We will denote by
$\mathcal {L}$. We will denote by ![]() $L$ the ample line bundle over
$L$ the ample line bundle over ![]() $X\!$ induced by
$X\!$ induced by ![]() $\mathcal {L};$ the polarized arithmetic variety
$\mathcal {L};$ the polarized arithmetic variety ![]() $(\mathcal {X},\mathcal {L})$ will be called a model for
$(\mathcal {X},\mathcal {L})$ will be called a model for ![]() $(X,L)$ over
$(X,L)$ over ![]() $\mathbb {Z}$ (or an integral model for
$\mathbb {Z}$ (or an integral model for ![]() $(X,L$)). We will use the following simple lemma.
$(X,L$)). We will use the following simple lemma.
Lemma 2.3 Under the assumptions above on ![]() $\mathcal {X}$ the canonical embedding of
$\mathcal {X}$ the canonical embedding of ![]() $\mathbb {Z}$ in
$\mathbb {Z}$ in ![]() $H^{0}(\mathcal {X},\mathcal {O}_{\mathcal {X}})$ is an isomorphism. In other words,
$H^{0}(\mathcal {X},\mathcal {O}_{\mathcal {X}})$ is an isomorphism. In other words, ![]() $1$ generates the
$1$ generates the ![]() $\mathbb {Z}$-module
$\mathbb {Z}$-module ![]() $H^{0}(\mathcal {X},\mathcal {O}_{\mathcal {X}})$.
$H^{0}(\mathcal {X},\mathcal {O}_{\mathcal {X}})$.
Proof. We have injections ![]() $\mathbb {Z}\hookrightarrow H^{0}(\mathcal {X},\mathcal {O}_{\mathcal {X}})\hookrightarrow H^{0}(X_{\mathbb {Q}},\mathcal {O}_{X_{\mathbb {Q}}})\simeq \mathbb {Q}$ (using flatness in the second injection and, in the isomorphism, that
$\mathbb {Z}\hookrightarrow H^{0}(\mathcal {X},\mathcal {O}_{\mathcal {X}})\hookrightarrow H^{0}(X_{\mathbb {Q}},\mathcal {O}_{X_{\mathbb {Q}}})\simeq \mathbb {Q}$ (using flatness in the second injection and, in the isomorphism, that ![]() $X_{\mathbb {Q}}$ is geometrically connected and geometrically reduced). But, since
$X_{\mathbb {Q}}$ is geometrically connected and geometrically reduced). But, since ![]() $H^{0}(\mathcal {X},\mathcal {O}_{\mathcal {X}})$ is a finitely generated
$H^{0}(\mathcal {X},\mathcal {O}_{\mathcal {X}})$ is a finitely generated ![]() $\mathbb {Z}$-module and
$\mathbb {Z}$-module and ![]() $\mathbb {Z}$ is an integrally closed domain this implies that
$\mathbb {Z}$ is an integrally closed domain this implies that ![]() $\mathbb {Z}\hookrightarrow H^{0}(\mathcal {X},\mathcal {O}_{\mathcal {X}})$ is an isomorphism.
$\mathbb {Z}\hookrightarrow H^{0}(\mathcal {X},\mathcal {O}_{\mathcal {X}})$ is an isomorphism.
For any positive integer ![]() $k$ we may identify the free
$k$ we may identify the free ![]() $\mathbb {Z}$-module
$\mathbb {Z}$-module ![]() $H^{0}(\mathcal {X},k\mathcal {L})$ with a lattice in
$H^{0}(\mathcal {X},k\mathcal {L})$ with a lattice in ![]() $H^{0}(X,kL)$:
$H^{0}(X,kL)$:
By definition a metrized line bundle ![]() $\overline {\mathcal {L}}$ is a line bundle
$\overline {\mathcal {L}}$ is a line bundle ![]() $\mathcal {L}\rightarrow \mathcal {X}$ such that the corresponding line bundle
$\mathcal {L}\rightarrow \mathcal {X}$ such that the corresponding line bundle ![]() $L\rightarrow X$ is endowed with a metric
$L\rightarrow X$ is endowed with a metric ![]() $\Vert \cdot \Vert$. We will use the additive notation
$\Vert \cdot \Vert$. We will use the additive notation ![]() $\phi$ for metrics
$\phi$ for metrics ![]() $\Vert \cdot \Vert$ on
$\Vert \cdot \Vert$ on ![]() $L$ discussed in the previous section:
$L$ discussed in the previous section:
2.2.1 Arithmetic Fano varieties
We will say that the relative canonical line bundle of an arithmetic variety ![]() $\mathcal {X}$ is defined as a
$\mathcal {X}$ is defined as a ![]() $\mathbb {Q}$-line bundle, denoted by
$\mathbb {Q}$-line bundle, denoted by ![]() $\mathcal {K},$ if there exists a positive integer
$\mathcal {K},$ if there exists a positive integer ![]() $m$ such that the
$m$ such that the ![]() $m$th reflexive power
$m$th reflexive power ![]() $\omega _{X/\mathrm {Spec}{\mathbb {Z}}}^{[m]}$ of the dualizing sheaf
$\omega _{X/\mathrm {Spec}{\mathbb {Z}}}^{[m]}$ of the dualizing sheaf ![]() $\omega _{X/\mathrm {Spec}{\mathbb {Z}}}$ of
$\omega _{X/\mathrm {Spec}{\mathbb {Z}}}$ of ![]() $\mathcal {X}$ is locally free. Then the line bundle
$\mathcal {X}$ is locally free. Then the line bundle ![]() $m\mathcal {K}$ over
$m\mathcal {K}$ over ![]() $\mathcal {X}$ may be identified with
$\mathcal {X}$ may be identified with ![]() $\omega _{X/\mathrm {Spec}{\mathbb {Z}}}^{[m]}$ (see [Reference KollárKol13, § 1.1] for a more general setup of canonical line bundles attached to schemes over regular excellent rings). An arithmetic variety
$\omega _{X/\mathrm {Spec}{\mathbb {Z}}}^{[m]}$ (see [Reference KollárKol13, § 1.1] for a more general setup of canonical line bundles attached to schemes over regular excellent rings). An arithmetic variety ![]() $\mathcal {X}\rightarrow \mathrm {Spec}{\mathbb {Z}}$ will be called an arithmetic Fano variety if:
$\mathcal {X}\rightarrow \mathrm {Spec}{\mathbb {Z}}$ will be called an arithmetic Fano variety if:
• the canonical line bundle
 $\mathcal {K}$ of
$\mathcal {K}$ of  $\mathcal {X}$ is well defined as a
$\mathcal {X}$ is well defined as a  $\mathbb {Q}$-line bundle and its dual
$\mathbb {Q}$-line bundle and its dual  $-\mathcal {K}$ is relatively ample;
$-\mathcal {K}$ is relatively ample;• the complexification
 $X\!$ of
$X\!$ of  $\mathcal {X}$ is normal and thus defines a complex Fano variety (i.e.
$\mathcal {X}$ is normal and thus defines a complex Fano variety (i.e.  $-K_{X\!}$ is ample)
$-K_{X\!}$ is ample)
Example 2.4 If ![]() $\mathcal {X}$ is locally a complete intersection, then
$\mathcal {X}$ is locally a complete intersection, then ![]() $\mathcal {K}$ is defined as a line bundle (i.e.
$\mathcal {K}$ is defined as a line bundle (i.e. ![]() $m=1)$ [Reference KollárKol13, § 1.1]. In particular, if
$m=1)$ [Reference KollárKol13, § 1.1]. In particular, if ![]() $\mathcal {X}$ is the subscheme of
$\mathcal {X}$ is the subscheme of ![]() $\mathbb {P}_{\mathbb {Z}}^{n+1}$ cut out by an irreducible homogeneous polynomial of degree
$\mathbb {P}_{\mathbb {Z}}^{n+1}$ cut out by an irreducible homogeneous polynomial of degree ![]() $d$ with integer coefficients, then
$d$ with integer coefficients, then ![]() $\mathcal {K}$ is well defined as a line bundle and
$\mathcal {K}$ is well defined as a line bundle and ![]() $\mathcal {X}$ is an arithmetic Fano variety if and only if
$\mathcal {X}$ is an arithmetic Fano variety if and only if ![]() $d\leq n+1$.
$d\leq n+1$.
2.2.2 The  $\chi$-arithmetic volume, heights and arithmetic intersection numbers
$\chi$-arithmetic volume, heights and arithmetic intersection numbers
In the arithmetic setup there are different analogs of the volume ![]() $\mathrm {vol}{(L)}$ of an ample line bundle
$\mathrm {vol}{(L)}$ of an ample line bundle ![]() $L$. Here we shall focus on the one defined by the following asymptotic arithmetic Euler characteristic originating in [Reference FaltingsFal84] (called the
$L$. Here we shall focus on the one defined by the following asymptotic arithmetic Euler characteristic originating in [Reference FaltingsFal84] (called the ![]() $\chi$-arithmetic volume in [Reference Burgos Gil, Philippon and SombraBPS14, Reference Burgos Gil, Moriwaki, Philippon and SombraBMPS16] and the sectional capacity in [Reference Rumely, Lau and VarleyRLV00]):
$\chi$-arithmetic volume in [Reference Burgos Gil, Philippon and SombraBPS14, Reference Burgos Gil, Moriwaki, Philippon and SombraBMPS16] and the sectional capacity in [Reference Rumely, Lau and VarleyRLV00]):
where the volume is computed with respect to the Lebesgue measure, normalized such that a fundamental domain of the lattice ![]() $H^{0}(\mathcal {X},k\mathcal {L})$ has unit volume. Here
$H^{0}(\mathcal {X},k\mathcal {L})$ has unit volume. Here ![]() $H^{0}(\mathcal {X},k\mathcal {L})\otimes \mathbb {R}$ may be identified with the subspace of real sections in
$H^{0}(\mathcal {X},k\mathcal {L})\otimes \mathbb {R}$ may be identified with the subspace of real sections in ![]() $H^{0}(X,kL)$. If the metric on
$H^{0}(X,kL)$. If the metric on ![]() $L$ has positive curvature current, then, by the arithmetic Hilbert–Samuel theorem [Reference Gillet and SouléGS92, Reference ZhangZha95],
$L$ has positive curvature current, then, by the arithmetic Hilbert–Samuel theorem [Reference Gillet and SouléGS92, Reference ZhangZha95],
 \begin{equation} \widehat{\mathrm{vol}}_{\chi}\bigl(\overline{\mathcal{L}}\bigr) =\frac{\overline{\mathcal{L}}^{n+1}}{(n+1)!},\end{equation}
\begin{equation} \widehat{\mathrm{vol}}_{\chi}\bigl(\overline{\mathcal{L}}\bigr) =\frac{\overline{\mathcal{L}}^{n+1}}{(n+1)!},\end{equation}
where ![]() $\overline {\mathcal {L}}^{n+1}$ denotes the top arithmetic intersection number in the sense of Gillet and Soulé [Reference Gillet and SouléGS90], which, defines the height of
$\overline {\mathcal {L}}^{n+1}$ denotes the top arithmetic intersection number in the sense of Gillet and Soulé [Reference Gillet and SouléGS90], which, defines the height of ![]() $\mathcal {X}$ with respect to
$\mathcal {X}$ with respect to ![]() $\overline {\mathcal {L}}$ [Reference FaltingsFal91, Reference Bost, Gillet and SouléBGS94]. For the purpose of the present paper, formula (2.5) may be taken as the definition of
$\overline {\mathcal {L}}$ [Reference FaltingsFal91, Reference Bost, Gillet and SouléBGS94]. For the purpose of the present paper, formula (2.5) may be taken as the definition of ![]() $\overline {\mathcal {L}}^{n+1}$ (arithmetic intersections between
$\overline {\mathcal {L}}^{n+1}$ (arithmetic intersections between ![]() $n+1$ metrized line bundles could then be defined by polarization). More generally,
$n+1$ metrized line bundles could then be defined by polarization). More generally, ![]() $\widehat {\mathrm {vol}}_{\chi }(\overline {\mathcal {L}})$ is naturally defined for
$\widehat {\mathrm {vol}}_{\chi }(\overline {\mathcal {L}})$ is naturally defined for ![]() $\mathbb {Q}$-line bundles, since it is homogeneous with respect to tensor products of
$\mathbb {Q}$-line bundles, since it is homogeneous with respect to tensor products of ![]() $\overline {\mathcal {L}}$:
$\overline {\mathcal {L}}$:
Moreover, ![]() $\widehat {\mathrm {vol}}_{\chi }(\overline {\mathcal {L}})$ is additively equivariant with respect to scalings of the metric:
$\widehat {\mathrm {vol}}_{\chi }(\overline {\mathcal {L}})$ is additively equivariant with respect to scalings of the metric:
as follows directly from the definition.
2.3 Upper bounds on the  $\chi$-arithmetic volume versus K-semistability of Fano varieties
$\chi$-arithmetic volume versus K-semistability of Fano varieties
We are now ready to prove the following theorem, relating upper bounds on the ![]() $\chi$-arithmetic volume of a metrized integral model of
$\chi$-arithmetic volume of a metrized integral model of ![]() $(X,-K_{X}\!)$ to K-semistability.
$(X,-K_{X}\!)$ to K-semistability.
Theorem 2.5 Let ![]() $(\mathcal {X},\mathcal {L})$ be a polarized arithmetic variety such that
$(\mathcal {X},\mathcal {L})$ be a polarized arithmetic variety such that ![]() $X\!$ is a Fano variety and
$X\!$ is a Fano variety and ![]() $L=-K_{X}$. Then the following statements are equivalent.
$L=-K_{X}$. Then the following statements are equivalent.
(1)
 $(X,-K_{X}\!)$ is K-semistable.
$(X,-K_{X}\!)$ is K-semistable.(2) The supremum of
 $\widehat {\mathrm {vol}}_{\chi }(\mathcal {L},\phi )$ over all continuous volume-normalized metrics
$\widehat {\mathrm {vol}}_{\chi }(\mathcal {L},\phi )$ over all continuous volume-normalized metrics  $\phi$ on
$\phi$ on  $-K_{X\!}$ is finite.
$-K_{X\!}$ is finite.(3) The supremum of
 $\widehat {\mathrm {vol}}_{\chi }(\mathcal {L},\phi )$ over all continuous volume-normalized metrics
$\widehat {\mathrm {vol}}_{\chi }(\mathcal {L},\phi )$ over all continuous volume-normalized metrics  $\phi$ on
$\phi$ on  $-K_{X}$, which are invariant under complex conjugation, is finite.
$-K_{X}$, which are invariant under complex conjugation, is finite.
Moreover, ![]() $(X,-K_{X}\!)$ is K-polystable if and only if the supremum in item (
$(X,-K_{X}\!)$ is K-polystable if and only if the supremum in item (![]() $2$) above is attained at some locally bounded metric
$2$) above is attained at some locally bounded metric ![]() $\psi$ in
$\psi$ in ![]() $\mathrm {PSH}{(-K_{X})}$. In general, a locally bounded metric
$\mathrm {PSH}{(-K_{X})}$. In general, a locally bounded metric ![]() $\psi$ in
$\psi$ in ![]() $\mathrm {PSH}{(-K_{X})}$ attains the supremum in item (
$\mathrm {PSH}{(-K_{X})}$ attains the supremum in item (![]() $2$) above if and only if it is a Kähler–Einstein metric.
$2$) above if and only if it is a Kähler–Einstein metric.
Recall that on any complex projective variety ![]() $X\!$ which is defined over
$X\!$ which is defined over ![]() $\mathbb {R}$ there is a globally defined complex conjugation map (whose orbits on
$\mathbb {R}$ there is a globally defined complex conjugation map (whose orbits on ![]() $X\!$ correspond to the maximal ideals of the scheme
$X\!$ correspond to the maximal ideals of the scheme ![]() $X_{\mathbb {R}})$ and in Arakelov geometry it is often assumed that the metrics are invariant under complex conjugation [Reference Soulé, Abramovich, Burnol and KramerSABK92].
$X_{\mathbb {R}})$ and in Arakelov geometry it is often assumed that the metrics are invariant under complex conjugation [Reference Soulé, Abramovich, Burnol and KramerSABK92].
Before embarking on the proof we recall the definition of the (normalized) Ding functional on ![]() $\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})},$ introduced in [Reference DingDin88], which depends on the choice of a reference metric
$\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})},$ introduced in [Reference DingDin88], which depends on the choice of a reference metric ![]() $\psi _{0}$ in
$\psi _{0}$ in ![]() $\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})}$:
$\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})}$:
where the functional ![]() $\mathcal {E}_{\psi _{0}}$ is a primitive of
$\mathcal {E}_{\psi _{0}}$ is a primitive of ![]() $(dd^{c}\psi )^{n}/n!$ (see formula (2.12)). More generally, as shown in [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19] using the monotonicity of
$(dd^{c}\psi )^{n}/n!$ (see formula (2.12)). More generally, as shown in [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19] using the monotonicity of ![]() $\mathcal {E}_{\psi _{0}}$,
$\mathcal {E}_{\psi _{0}}$, ![]() $\mathcal {\hat {D}}_{\psi _{0}}(\psi )$ can be extended to the space
$\mathcal {\hat {D}}_{\psi _{0}}(\psi )$ can be extended to the space ![]() $\mathcal {E}^{1}(-K_{X}\!)$ of all metrics in
$\mathcal {E}^{1}(-K_{X}\!)$ of all metrics in ![]() $\mathrm {PSH}{(-K_{X})}$ with finite energy and a finite energy metric
$\mathrm {PSH}{(-K_{X})}$ with finite energy and a finite energy metric ![]() $\psi$ minimizes
$\psi$ minimizes ![]() $\mathcal {\hat {D}}_{\psi _{0}}(\psi )$ if and only if
$\mathcal {\hat {D}}_{\psi _{0}}(\psi )$ if and only if ![]() $\psi$ is a Kähler–Einstein metric, i.e.
$\psi$ is a Kähler–Einstein metric, i.e. ![]() $dd^{c}\psi$ defines a Kähler metric on the regular locus of
$dd^{c}\psi$ defines a Kähler metric on the regular locus of ![]() $X\!$ with constant positive Ricci curvature. When
$X\!$ with constant positive Ricci curvature. When ![]() $\psi$ is volume-normalized this equivalently means that
$\psi$ is volume-normalized this equivalently means that
on the regular locus of ![]() $X$. Identity (2.6) was extended to finite energy metrics in [Reference Berman and Freixas i MontpletBF14]. But for our purposes it will be enough to work with continuous metrics.
$X$. Identity (2.6) was extended to finite energy metrics in [Reference Berman and Freixas i MontpletBF14]. But for our purposes it will be enough to work with continuous metrics.
Remark 2.6 In general, any Kähler–Einstein metric ![]() $\psi$ in
$\psi$ in ![]() $\mathcal {E}^{1}(-K_{X}\!)$ is locally bounded [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19]. In the toric case this implies that
$\mathcal {E}^{1}(-K_{X}\!)$ is locally bounded [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19]. In the toric case this implies that ![]() $\psi$ is, in fact, continuous [Reference Coman, Guedj and SahinCGS19, Proposition 4.1].
$\psi$ is, in fact, continuous [Reference Coman, Guedj and SahinCGS19, Proposition 4.1].
By introducing an arithmetic version of the Ding functional we show that item (![]() $2$) in the previous theorem is equivalent to the normalized Ding functional
$2$) in the previous theorem is equivalent to the normalized Ding functional ![]() $\mathcal {\hat {D}}_{\psi _{0}}$ being bounded from below on
$\mathcal {\hat {D}}_{\psi _{0}}$ being bounded from below on ![]() $\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})}$ (which is equivalent to lower boundedness of the Mabuchi functional; see (4.7)). By [Reference LiLi17] this is equivalent to K-semistability when
$\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})}$ (which is equivalent to lower boundedness of the Mabuchi functional; see (4.7)). By [Reference LiLi17] this is equivalent to K-semistability when ![]() $X\!$ is non-singular. In the proof of Theorem 2.5 we explain how to extend this result to general Fano varieties, leveraging the very recent solution of the Yau–Tian–Donaldson conjecture for singular Fano varieties [Reference LiLi22, Reference Liu, Xu and ZhuangLXZ22]. The equivalence with item (
$X\!$ is non-singular. In the proof of Theorem 2.5 we explain how to extend this result to general Fano varieties, leveraging the very recent solution of the Yau–Tian–Donaldson conjecture for singular Fano varieties [Reference LiLi22, Reference Liu, Xu and ZhuangLXZ22]. The equivalence with item (![]() $3$) leverages the recent result [Reference ZhuangZhu21].
$3$) leverages the recent result [Reference ZhuangZhu21].
2.3.1 Proof of Theorem 2.5
We start with two lemmas. First, to a given continuous metric ![]() $\phi$ on
$\phi$ on ![]() $L$ we associate, following [Reference Berman and BoucksomBB10], a continuous psh metric
$L$ we associate, following [Reference Berman and BoucksomBB10], a continuous psh metric ![]() $\psi$ on
$\psi$ on ![]() $L$ defined as the following pointwise envelope:
$L$ defined as the following pointwise envelope:
Remark 2.7 More generally, when ![]() $L$ is big the envelope above has to be replaced by its upper semicontinuous regularization in order to obtain a psh metric. However, when
$L$ is big the envelope above has to be replaced by its upper semicontinuous regularization in order to obtain a psh metric. However, when ![]() $L$ is an ample line bundle over a normal variety
$L$ is an ample line bundle over a normal variety ![]() $X,$ as we assume here, the envelope
$X,$ as we assume here, the envelope ![]() $P\phi$ is already continuous (see [Reference Boucksom and ErikssonBE21, Lemma 7.9]).
$P\phi$ is already continuous (see [Reference Boucksom and ErikssonBE21, Lemma 7.9]).
Lemma 2.8 Assume that ![]() $\mathcal {L}$ is relatively ample and let
$\mathcal {L}$ is relatively ample and let ![]() $\phi$ be a continuous metric on
$\phi$ be a continuous metric on ![]() $L$. Then the arithmetic
$L$. Then the arithmetic ![]() $\chi$-volume may be expressed as the following top arithmetic intersection number:
$\chi$-volume may be expressed as the following top arithmetic intersection number:
Proof. When ![]() $\phi$ is psh the lemma follows directly from [Reference ZhangZha95, Theorem 1.4] (the latter proof reduces to the original arithmetic Hilbert–Samuel theorem in [Reference Gillet and SouléGS92], where
$\phi$ is psh the lemma follows directly from [Reference ZhangZha95, Theorem 1.4] (the latter proof reduces to the original arithmetic Hilbert–Samuel theorem in [Reference Gillet and SouléGS92], where ![]() $X\!$ is assumed non-singular, using a perturbation argument on a resolution of
$X\!$ is assumed non-singular, using a perturbation argument on a resolution of ![]() $X)$. In fact, the result [Reference ZhangZha95, Theorem 1.4] applies more generally when
$X)$. In fact, the result [Reference ZhangZha95, Theorem 1.4] applies more generally when ![]() $\mathcal {L}$ is merely assumed to be relatively nef over the closed points of
$\mathcal {L}$ is merely assumed to be relatively nef over the closed points of ![]() $\mathrm {Spec}{\mathbb {Z}}$. Next, the general case follows from the case when
$\mathrm {Spec}{\mathbb {Z}}$. Next, the general case follows from the case when ![]() $\phi$ is psh (applied to
$\phi$ is psh (applied to ![]() $P\phi )$ by the following simple observation:
$P\phi )$ by the following simple observation:
as follows directly from the definition (2.10) of ![]() $P\phi$ (see [Reference Berman and BoucksomBB10, Proposition 1.8]).
$P\phi$ (see [Reference Berman and BoucksomBB10, Proposition 1.8]).
In order to state the next lemma consider the following functional on ![]() $\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)},$ defined with respect to a given reference
$\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)},$ defined with respect to a given reference ![]() $\psi _{0}\in \mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$:
$\psi _{0}\in \mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$:
 \begin{equation} \mathcal{E}_{\psi_{0}}(\psi):=\frac{1}{(n+1)!}\int_{X}(\psi-\psi_{0})\sum_{j=0}^{n}(dd^{c}\psi)^{j}\wedge(dd^{c}\psi_{0})^{n-j}. \end{equation}
\begin{equation} \mathcal{E}_{\psi_{0}}(\psi):=\frac{1}{(n+1)!}\int_{X}(\psi-\psi_{0})\sum_{j=0}^{n}(dd^{c}\psi)^{j}\wedge(dd^{c}\psi_{0})^{n-j}. \end{equation}
Alternatively, the functional ![]() $\mathcal {E}_{\psi _{0}}$ may be characterized as the primitive of the
$\mathcal {E}_{\psi _{0}}$ may be characterized as the primitive of the ![]() $1$-form on
$1$-form on ![]() $\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$ defined by the measure
$\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$ defined by the measure ![]() $(dd^{c}\psi )^{n}/n!$:
$(dd^{c}\psi )^{n}/n!$:
It follows directly from the definition of ![]() $\mathcal {E}_{\psi _{0}}(\psi )$ and the classical Hilbert–Samuel formula (2.2) that
$\mathcal {E}_{\psi _{0}}(\psi )$ and the classical Hilbert–Samuel formula (2.2) that
The following lemma is an arithmetic refinement of the previous formula.
Lemma 2.9 (Change of metrics formula)
For any two continuous metrics on ![]() $L,$ which are invariant under complex conjugation,
$L,$ which are invariant under complex conjugation,
Proof. When ![]() $\phi _{i}$ are psh this is well known and follows from basic properties of arithmetic intersection numbers; see formula (5.2) or [Reference OdakaOda18, Proposition 2.2]). Alternatively, the result follows from the previous lemma combined with [Reference Berman and BoucksomBB10, Theorem A]. In order to check that the multiplicative normalizations adopted here are compatible, note that the scaling relations (2.8) and (2.13) are indeed compatible.
$\phi _{i}$ are psh this is well known and follows from basic properties of arithmetic intersection numbers; see formula (5.2) or [Reference OdakaOda18, Proposition 2.2]). Alternatively, the result follows from the previous lemma combined with [Reference Berman and BoucksomBB10, Theorem A]. In order to check that the multiplicative normalizations adopted here are compatible, note that the scaling relations (2.8) and (2.13) are indeed compatible.
2.3.2 Conclusion of the proof of Theorem 2.5
Consider the following functional on the space ![]() $\mathcal {C}^{0}(-K_{X}\!)$ of continuous metrics on
$\mathcal {C}^{0}(-K_{X}\!)$ of continuous metrics on ![]() $-K_{X\!}$:
$-K_{X\!}$:
 \begin{equation} \mathcal{\hat{D}}_{\mathbb{Z}}(\phi):=-2\frac{\widehat{\mathrm{vol}}_{\chi}(\mathcal{L},\phi)}{\mathrm{vol}(-K_{X})}-\log\int_{X}e^{-\phi}.\end{equation}
\begin{equation} \mathcal{\hat{D}}_{\mathbb{Z}}(\phi):=-2\frac{\widehat{\mathrm{vol}}_{\chi}(\mathcal{L},\phi)}{\mathrm{vol}(-K_{X})}-\log\int_{X}e^{-\phi}.\end{equation}
Since this functional is invariant under scalings of the metric, ![]() $\phi \mapsto \phi +c,$ the finiteness statement in the second point of the theorem amounts to showing that the infimum of
$\phi \mapsto \phi +c,$ the finiteness statement in the second point of the theorem amounts to showing that the infimum of ![]() $\mathcal {\hat {D}}_{\mathbb {Z}}(\phi )$ over
$\mathcal {\hat {D}}_{\mathbb {Z}}(\phi )$ over ![]() $\mathcal {C}^{0}(-K_{X}\!)$ is finite. Now fix a continuous psh metric
$\mathcal {C}^{0}(-K_{X}\!)$ is finite. Now fix a continuous psh metric ![]() $\psi _{0}$ on
$\psi _{0}$ on ![]() $-K_{X\!}$ and consider the following extension of the normalized Ding functional (2.9) to all of
$-K_{X\!}$ and consider the following extension of the normalized Ding functional (2.9) to all of ![]() $\mathcal {C}^{0}(-K_{X}\!)$:
$\mathcal {C}^{0}(-K_{X}\!)$:
Combining the previous two lemmas reveals that
 \begin{equation} \mathcal{\hat{D}}_{\mathbb{Z}}(\phi)=\mathcal{\hat{D}}_{\psi_{0}}(\phi)+C_{0},\quad C_{0}:=-\frac{2\big(\mathcal{L},\psi_{0}\big)^{n+1}}{\mathrm{vol}(-K_{X})(n+1)!}. \end{equation}
\begin{equation} \mathcal{\hat{D}}_{\mathbb{Z}}(\phi)=\mathcal{\hat{D}}_{\psi_{0}}(\phi)+C_{0},\quad C_{0}:=-\frac{2\big(\mathcal{L},\psi_{0}\big)^{n+1}}{\mathrm{vol}(-K_{X})(n+1)!}. \end{equation}Next, observe that
Indeed, this follows directly from the fact that the operator ![]() $\phi \mapsto P\phi$ from
$\phi \mapsto P\phi$ from ![]() $\mathcal {C}^{0}(L)$ to
$\mathcal {C}^{0}(L)$ to ![]() $\mathcal {C}^{0}(L)\Cap \mathrm {PSH}{(L)}$ is increasing and satisfies
$\mathcal {C}^{0}(L)\Cap \mathrm {PSH}{(L)}$ is increasing and satisfies ![]() $P^{2}=P$.
$P^{2}=P$.
 $(3)\implies (1)$
$(3)\implies (1)$
Let us first recall how item (![]() $2$) implies item (
$2$) implies item (![]() $1$). Item (
$1$). Item (![]() $2$) implies, thanks to the identities (2.17) and (2.18), that the infimum of
$2$) implies, thanks to the identities (2.17) and (2.18), that the infimum of ![]() $\mathcal {\hat {D}}_{\psi _{0}}$ over
$\mathcal {\hat {D}}_{\psi _{0}}$ over ![]() $\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})}$ is finite. Thus it follows from results in [Reference BermanBer16] that
$\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})}$ is finite. Thus it follows from results in [Reference BermanBer16] that ![]() $(X,-K_{X}\!)$ is K-semistable. Let us next show how to refine the proof in [Reference BermanBer16] to show the stronger statement
$(X,-K_{X}\!)$ is K-semistable. Let us next show how to refine the proof in [Reference BermanBer16] to show the stronger statement ![]() $(3)\implies (1)$. More generally, we will show that when
$(3)\implies (1)$. More generally, we will show that when ![]() $X\!$ is defined over the real field
$X\!$ is defined over the real field ![]() $\mathbb {R}$,
$\mathbb {R}$, ![]() $X\!$ is K-semistable if the infimum of
$X\!$ is K-semistable if the infimum of ![]() $\mathcal {\hat {D}}_{\psi _{0}}$ over the space
$\mathcal {\hat {D}}_{\psi _{0}}$ over the space ![]() $\overline {\mathcal {C}^{0}(-K_{X})}\Cap \mathrm {PSH}{(-K_{X})}$ is finite, where
$\overline {\mathcal {C}^{0}(-K_{X})}\Cap \mathrm {PSH}{(-K_{X})}$ is finite, where ![]() $\overline {\mathcal {C}^{0}(L)}$ denotes the subspace of
$\overline {\mathcal {C}^{0}(L)}$ denotes the subspace of ![]() $\mathcal {C}^{0}(L)$ consisting of metrics which are invariant under complex conjugation. To this end, let us first summarize the main steps in the proof in [Reference BermanBer16]. A test configuration
$\mathcal {C}^{0}(L)$ consisting of metrics which are invariant under complex conjugation. To this end, let us first summarize the main steps in the proof in [Reference BermanBer16]. A test configuration ![]() $(\mathscr {X},\mathscr {L})$ for
$(\mathscr {X},\mathscr {L})$ for ![]() $(X,-K_{X}\!)$ and a given metric
$(X,-K_{X}\!)$ and a given metric ![]() $\phi$ for
$\phi$ for ![]() $-K_{X\!}$ in
$-K_{X\!}$ in ![]() $\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})}$ determine a ray
$\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})}$ determine a ray ![]() $\phi _{t}$ in
$\phi _{t}$ in ![]() $\mathrm {PSH}{(-K_{X})}$ emanating from
$\mathrm {PSH}{(-K_{X})}$ emanating from ![]() $\phi$ parametrized by
$\phi$ parametrized by ![]() $t\in [0,\infty [$ (i.e.
$t\in [0,\infty [$ (i.e. ![]() $\phi _{0}=\phi )$. Using the notation in formula (2.4), the ray
$\phi _{0}=\phi )$. Using the notation in formula (2.4), the ray ![]() $\phi _{t}$ is defined by
$\phi _{t}$ is defined by
where ![]() $\Phi$ is the
$\Phi$ is the ![]() $S^{1}$-invariant metric on the restriction of
$S^{1}$-invariant metric on the restriction of ![]() $\mathcal {L}$ to the inverse image
$\mathcal {L}$ to the inverse image ![]() $\pi ^{-1}(\mathbb {D})$ in
$\pi ^{-1}(\mathbb {D})$ in ![]() $\mathcal {X}$ of the unit disc
$\mathcal {X}$ of the unit disc ![]() $\mathbb {D}\subset \mathbb {C}$ defined by
$\mathbb {D}\subset \mathbb {C}$ defined by
where we have used the ![]() $\mathbb {C}^{*}$-action
$\mathbb {C}^{*}$-action ![]() $\rho$ to identify
$\rho$ to identify ![]() $X\!$ with
$X\!$ with ![]() $X_{\tau }$ for any
$X_{\tau }$ for any ![]() $\tau$ in the unit circle
$\tau$ in the unit circle ![]() $\partial \mathbb {D}$. By [Reference BermanBer16, Theorem 1.3],
$\partial \mathbb {D}$. By [Reference BermanBer16, Theorem 1.3],
When ![]() $\mathcal {\hat {D}}_{\phi _{0}}(\phi _{t})$ is bounded from below this means that
$\mathcal {\hat {D}}_{\phi _{0}}(\phi _{t})$ is bounded from below this means that ![]() $\mathrm {DF}(\mathscr {X},\mathscr {L})\geq 0,$ showing that
$\mathrm {DF}(\mathscr {X},\mathscr {L})\geq 0,$ showing that ![]() $X\!$ is K-semistable. Now assume that
$X\!$ is K-semistable. Now assume that ![]() $X\!$ is defined over the real field
$X\!$ is defined over the real field ![]() $\mathbb {R}$. Then it follows from [Reference ZhuangZhu21, Theorem 1.1] that in order to check K-semistability of
$\mathbb {R}$. Then it follows from [Reference ZhuangZhu21, Theorem 1.1] that in order to check K-semistability of ![]() $(X,-K_{X}\!)$ it is enough to consider test configurations
$(X,-K_{X}\!)$ it is enough to consider test configurations ![]() $(\mathscr {X},\mathscr {L})$ defined over
$(\mathscr {X},\mathscr {L})$ defined over ![]() $\mathbb {R}$. Thus, we just have to verify that for such test configurations, if the given metric
$\mathbb {R}$. Thus, we just have to verify that for such test configurations, if the given metric ![]() $\phi$ is taken to be in
$\phi$ is taken to be in ![]() $\overline {\mathcal {C}^{0}(-K_{X})}\Cap \mathrm {PSH}{(-K_{X})},$ then the ray
$\overline {\mathcal {C}^{0}(-K_{X})}\Cap \mathrm {PSH}{(-K_{X})},$ then the ray ![]() $\phi _{t}$ remains in
$\phi _{t}$ remains in ![]() $\overline {\mathcal {C}^{0}(-K_{X})}\Cap \mathrm {PSH}{(-K_{X})},$ for all
$\overline {\mathcal {C}^{0}(-K_{X})}\Cap \mathrm {PSH}{(-K_{X})},$ for all ![]() $t>0$. Since
$t>0$. Since ![]() $(\mathscr {X},\mathscr {L})$ is defined over
$(\mathscr {X},\mathscr {L})$ is defined over ![]() $\mathbb {R}$ there is a complex conjugation map
$\mathbb {R}$ there is a complex conjugation map ![]() $F$ from
$F$ from ![]() $\mathscr {X\!}$ to
$\mathscr {X\!}$ to ![]() $\mathscr {X\!}$ (which lifts to
$\mathscr {X\!}$ (which lifts to ![]() $\mathscr {L})$ and thus it is enough to show that
$\mathscr {L})$ and thus it is enough to show that ![]() $F^{*}\phi =\phi$ implies that
$F^{*}\phi =\phi$ implies that ![]() $F^{*}\Phi =\Phi$. But this follows from the definition (2.19) of
$F^{*}\Phi =\Phi$. But this follows from the definition (2.19) of ![]() $\Phi$ only using that
$\Phi$ only using that ![]() $F^{*}$ preserves the psh property of a metric (as follows from a direct local calculation that reduces to the fact that the Laplacian
$F^{*}$ preserves the psh property of a metric (as follows from a direct local calculation that reduces to the fact that the Laplacian ![]() $i\partial _{z}\partial _{\bar {z}}$ in
$i\partial _{z}\partial _{\bar {z}}$ in ![]() $\mathbb {C}$ is invariant under
$\mathbb {C}$ is invariant under ![]() $z\mapsto \bar {z})$.
$z\mapsto \bar {z})$.
 $(1)\implies (2)$
$(1)\implies (2)$
Recall that any K-semistable normal Fano variety (i.e. such that ![]() $(X,-K_{X}\!)$ is K-semistable) has log terminal singularities [Reference OdakaOda13b, Theorem 1.3]. In the case when
$(X,-K_{X}\!)$ is K-semistable) has log terminal singularities [Reference OdakaOda13b, Theorem 1.3]. In the case when ![]() $X\!$ is non-singular it was shown in [Reference LiLi17] that if
$X\!$ is non-singular it was shown in [Reference LiLi17] that if ![]() $X\!$ is K-semistable, then the infimum of the Ding functional
$X\!$ is K-semistable, then the infimum of the Ding functional ![]() $\mathcal {\hat {D}}_{\psi _{0}}$ over
$\mathcal {\hat {D}}_{\psi _{0}}$ over ![]() $\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})}$ is finite. Thus, by formula (2.18), so is the infimum of
$\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})}$ is finite. Thus, by formula (2.18), so is the infimum of ![]() $\mathcal {\hat {D}}_{\psi _{0}}$ over
$\mathcal {\hat {D}}_{\psi _{0}}$ over ![]() $\mathcal {C}^{0}(-K_{X}\!)$. The proof in [Reference LiLi17] relied, in particular, on the resolution of the Yau–Tian–Donaldson conjecture in [Reference Chen, Donaldson and SunCDS15] for Fano manifolds. But thanks to the recent resolution of the Yau–Tian–Donaldson conjecture for singular Fano varieties the proof in [Reference LiLi17] can be extended to singular Fano varieties, mutatis mutandis. We briefly summarize the argument, using Deligne pairings as in [Reference BermanBer16] (rather than the Bott–Chern classes used in [Reference LiLi17]). The starting point is the result [Reference Li, Wang and XuLWX21, Theorem 1.3], saying that if
$\mathcal {C}^{0}(-K_{X}\!)$. The proof in [Reference LiLi17] relied, in particular, on the resolution of the Yau–Tian–Donaldson conjecture in [Reference Chen, Donaldson and SunCDS15] for Fano manifolds. But thanks to the recent resolution of the Yau–Tian–Donaldson conjecture for singular Fano varieties the proof in [Reference LiLi17] can be extended to singular Fano varieties, mutatis mutandis. We briefly summarize the argument, using Deligne pairings as in [Reference BermanBer16] (rather than the Bott–Chern classes used in [Reference LiLi17]). The starting point is the result [Reference Li, Wang and XuLWX21, Theorem 1.3], saying that if ![]() $X\!$ is K-semistable then there exists a test configuration
$X\!$ is K-semistable then there exists a test configuration ![]() $(\mathscr {X},\mathscr {L})$ for
$(\mathscr {X},\mathscr {L})$ for ![]() $(X,-K_{X}\!)$ whose central fiber
$(X,-K_{X}\!)$ whose central fiber ![]() $X_{0}$ is given by a K-polystable Fano variety. More precisely, the test configuration is special in the sense that
$X_{0}$ is given by a K-polystable Fano variety. More precisely, the test configuration is special in the sense that ![]() $\mathscr {L}$ is the relative anti-canonical line bundle. Since the central fiber
$\mathscr {L}$ is the relative anti-canonical line bundle. Since the central fiber ![]() $X_{0}$ of
$X_{0}$ of ![]() $\mathscr {X\!}$ is K-polystable it admits, by the solution of the Yau–Tian–Donaldson conjecture for singular Fano varieties [Reference Liu, Xu and ZhuangLXZ22] (building on [Reference LiLi22]), a Kähler–Einstein metric
$\mathscr {X\!}$ is K-polystable it admits, by the solution of the Yau–Tian–Donaldson conjecture for singular Fano varieties [Reference Liu, Xu and ZhuangLXZ22] (building on [Reference LiLi22]), a Kähler–Einstein metric ![]() $\phi _{\mathrm {KE}}$. It thus follows from [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19, Theorem 4.8] that the Ding functional is bounded from below on
$\phi _{\mathrm {KE}}$. It thus follows from [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19, Theorem 4.8] that the Ding functional is bounded from below on ![]() $\mathcal {C}^{0}(-K_{X_{0}})\Cap \mathrm {PSH}(-K_{X_{0}})$. More precisely, its infimum is attained at the Kähler–Einstein metric
$\mathcal {C}^{0}(-K_{X_{0}})\Cap \mathrm {PSH}(-K_{X_{0}})$. More precisely, its infimum is attained at the Kähler–Einstein metric ![]() $\phi _{\mathrm {KE}}$:
$\phi _{\mathrm {KE}}$:
Now, given a metric ![]() $\phi$ in
$\phi$ in ![]() $\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})}$, let
$\mathcal {C}^{0}(-K_{X})\Cap \mathrm {PSH}{(-K_{X})}$, let ![]() $\Phi$ be the corresponding metric on
$\Phi$ be the corresponding metric on ![]() $\mathscr {L}\rightarrow \pi ^{-1}(\mathbb {D})$ defined by formula (2.19). It induces a metric on the
$\mathscr {L}\rightarrow \pi ^{-1}(\mathbb {D})$ defined by formula (2.19). It induces a metric on the ![]() $(n+1)$-fold Deligne pairing
$(n+1)$-fold Deligne pairing ![]() $\langle \mathscr {L},\mathscr {L},\ldots,\mathscr {L}\rangle \rightarrow \mathbb {D}$ that we denote by
$\langle \mathscr {L},\mathscr {L},\ldots,\mathscr {L}\rangle \rightarrow \mathbb {D}$ that we denote by ![]() $\langle \Phi \rangle$ (see [Reference BermanBer16, § 2.3]). Consider the corresponding twisted metric on
$\langle \Phi \rangle$ (see [Reference BermanBer16, § 2.3]). Consider the corresponding twisted metric on ![]() $-\langle \mathscr {L},\mathscr {L},\ldots,\mathscr {L}\rangle \rightarrow \mathbb {D}$ defined by
$-\langle \mathscr {L},\mathscr {L},\ldots,\mathscr {L}\rangle \rightarrow \mathbb {D}$ defined by
dubbed the Ding metric in [Reference BermanBer16]. Fixing a trivialization ![]() $S(\tau )$ of
$S(\tau )$ of ![]() $\langle \mathscr {L},\mathscr {L},\ldots,\mathscr {L}\rangle \rightarrow \mathbb {D}$, we may identify this metric with a function
$\langle \mathscr {L},\mathscr {L},\ldots,\mathscr {L}\rangle \rightarrow \mathbb {D}$, we may identify this metric with a function ![]() $\psi (\tau )$ on
$\psi (\tau )$ on ![]() $\mathbb {D}$:
$\mathbb {D}$:
For a fixed ![]() $\tau$ this metric coincides with the normalized Ding functional
$\tau$ this metric coincides with the normalized Ding functional ![]() $\mathcal {\hat {D}}(\phi _{\tau })$ up to an additive constant depending on
$\mathcal {\hat {D}}(\phi _{\tau })$ up to an additive constant depending on ![]() $\tau$ (by the ‘change of metrics formula’ for Deligne pairing; see [Reference BermanBer16, § 2.3]). In particular, there exists
$\tau$ (by the ‘change of metrics formula’ for Deligne pairing; see [Reference BermanBer16, § 2.3]). In particular, there exists ![]() $a\in \mathbb {R}$ such that
$a\in \mathbb {R}$ such that
using (2.20) in the inequality. As shown in [Reference BermanBer16, Proposition 3.5], ![]() $\psi (\tau )$ is subharmonic on
$\psi (\tau )$ is subharmonic on ![]() $\mathbb {D}$ and the first term
$\mathbb {D}$ and the first term ![]() $\langle \Phi \rangle$ is continuous on
$\langle \Phi \rangle$ is continuous on ![]() $\mathbb {D}$ (as follows from [Reference MoriwakiMor99, Theorem A]; see the proof of [Reference BermanBer16, Proposition 3.6]). Moreover, the second term is also continuous on
$\mathbb {D}$ (as follows from [Reference MoriwakiMor99, Theorem A]; see the proof of [Reference BermanBer16, Proposition 3.6]). Moreover, the second term is also continuous on ![]() $\mathbb {D},$ as shown when
$\mathbb {D},$ as shown when ![]() $X\!$ is non-singular in [Reference LiLi17, Lemma 1.9] and in general in [Reference Li, Wang and XuLWX18, Lemma 7.1]. As a consequence,
$X\!$ is non-singular in [Reference LiLi17, Lemma 1.9] and in general in [Reference Li, Wang and XuLWX18, Lemma 7.1]. As a consequence,
using that ![]() $\psi (\tau )$ is
$\psi (\tau )$ is ![]() $S^{1}$-invariant in the last equality. Finally, invoking formula (2.21) shows that
$S^{1}$-invariant in the last equality. Finally, invoking formula (2.21) shows that ![]() $\mathcal {\hat {D}}_{\psi _{0}}(\phi )$ is uniformly bounded from below, as desired.
$\mathcal {\hat {D}}_{\psi _{0}}(\phi )$ is uniformly bounded from below, as desired.
2.4 Compatibility of Conjecture 1.1 with taking products
The previous theorem shows, in particular, that the K-semistability assumption in Conjecture 1.1 is necessary. We next show that the conjecture is compatible with taking products.
Proposition 2.10 Let ![]() $m\geq 2$ and
$m\geq 2$ and ![]() $\mathcal {X}_{1},\ldots,\mathcal {X}_{m}$ be arithmetic Fano varieties which are K-semistable over
$\mathcal {X}_{1},\ldots,\mathcal {X}_{m}$ be arithmetic Fano varieties which are K-semistable over ![]() $\mathbb {C}$. Assume that the inequality in Conjecture 1.1 holds for all
$\mathbb {C}$. Assume that the inequality in Conjecture 1.1 holds for all ![]() $\mathcal {X}_{i}$ (for any volume-normalized metrics on
$\mathcal {X}_{i}$ (for any volume-normalized metrics on ![]() $-K_{X_{i}}$ with positive curvature current). Then the inequality holds for
$-K_{X_{i}}$ with positive curvature current). Then the inequality holds for ![]() $\mathcal {X}_{1}\times \cdots \times \mathcal {X}_{m}$ with strict inequality (for any volume-normalized metric on
$\mathcal {X}_{1}\times \cdots \times \mathcal {X}_{m}$ with strict inequality (for any volume-normalized metric on ![]() $-K_{X_{1}\times \cdots \times X_{m}}$ with positive curvature current). More precisely,
$-K_{X_{1}\times \cdots \times X_{m}}$ with positive curvature current). More precisely,
Proof. By a simple induction argument it is enough to consider the case when ![]() $m=2$. Note that, in general, given two polarized metrized arithmetic varieties
$m=2$. Note that, in general, given two polarized metrized arithmetic varieties ![]() $(\mathcal {X}_{i},\overline {\mathcal {L}_{i}})$ of relative dimension
$(\mathcal {X}_{i},\overline {\mathcal {L}_{i}})$ of relative dimension ![]() $n_{i}$
$n_{i}$
 \begin{equation} \frac{\widehat{\mathrm{vol}}_{\chi}\bigl(\rho_{1}^{*}\overline{\mathcal{L}_{1}}\otimes\rho_{2}^{*}\overline{\mathcal{L}_{2}}\bigr)} {\mathrm{vol} \bigl(\rho_{1}^{*}\overline{\mathcal{L}_{1}}\otimes\rho_{2}^{*}\overline{\mathcal{L}_{2}}\bigr)} = \frac{\widehat{\mathrm{vol}}_{\chi}(\overline{\mathcal{L}_{1}})}{\mathrm{vol} \bigl(\overline{\mathcal{L}_{1}}\bigr)} +\frac{\widehat{\mathrm{vol}}_{\chi}\bigl(\overline{\mathcal{L}_{2}}\bigr)}{\mathrm{vol} \bigl(\overline{\mathcal{L}_{2}}\bigr)}, \end{equation}
\begin{equation} \frac{\widehat{\mathrm{vol}}_{\chi}\bigl(\rho_{1}^{*}\overline{\mathcal{L}_{1}}\otimes\rho_{2}^{*}\overline{\mathcal{L}_{2}}\bigr)} {\mathrm{vol} \bigl(\rho_{1}^{*}\overline{\mathcal{L}_{1}}\otimes\rho_{2}^{*}\overline{\mathcal{L}_{2}}\bigr)} = \frac{\widehat{\mathrm{vol}}_{\chi}(\overline{\mathcal{L}_{1}})}{\mathrm{vol} \bigl(\overline{\mathcal{L}_{1}}\bigr)} +\frac{\widehat{\mathrm{vol}}_{\chi}\bigl(\overline{\mathcal{L}_{2}}\bigr)}{\mathrm{vol} \bigl(\overline{\mathcal{L}_{2}}\bigr)}, \end{equation}
where ![]() $\rho _{1}$ and
$\rho _{1}$ and ![]() $\rho _{2}$ denote the natural morphisms from
$\rho _{2}$ denote the natural morphisms from ![]() $\mathcal {X}_{1}\times \mathcal {X}_{2}$ to
$\mathcal {X}_{1}\times \mathcal {X}_{2}$ to ![]() $\mathcal {X}_{1}$ and
$\mathcal {X}_{1}$ and ![]() $\mathcal {X}_{2},$ respectively (as follows readily from formula (2.5)).
$\mathcal {X}_{2},$ respectively (as follows readily from formula (2.5)).
Assume now that the inequality in Conjecture 1.1 holds for ![]() $\overline {-\mathcal {K}_{\mathcal {X}_{1}}}$ and
$\overline {-\mathcal {K}_{\mathcal {X}_{1}}}$ and ![]() $\overline {-\mathcal {K}_{\mathcal {X}_{2}}}$. Endow
$\overline {-\mathcal {K}_{\mathcal {X}_{2}}}$. Endow ![]() $-K_{X_{1}\times X_{2}}$ with the induced product metric (which is volume-normalized, since the metrics on
$-K_{X_{1}\times X_{2}}$ with the induced product metric (which is volume-normalized, since the metrics on ![]() $-K_{X_{i}}$ are assumed to be volume-normalized). Identity (2.22) yields
$-K_{X_{i}}$ are assumed to be volume-normalized). Identity (2.22) yields
Accordingly, by assumption,
where the projective spaces have been induced by the volume-normalized Fubini–Study metric and we have used that ![]() $\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n}}})$ is positive for any
$\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n}}})$ is positive for any ![]() $n$ (as shown in Lemma 3.6). Hence, applying Fujita's inequality (1.1) yields
$n$ (as shown in Lemma 3.6). Hence, applying Fujita's inequality (1.1) yields
But, the right-hand side above equals ![]() $\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n_{1}}\times \mathbb {P}_{\mathbb {Z}}^{n_{2}}}})$ (by identity (2.22)), which is strictly smaller than
$\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n_{1}}\times \mathbb {P}_{\mathbb {Z}}^{n_{2}}}})$ (by identity (2.22)), which is strictly smaller than ![]() $\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n_{1}+n_{2}}}}),$ by the toric case, considered in § 3.2.2.
$\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n_{1}+n_{2}}}}),$ by the toric case, considered in § 3.2.2.
All that remains is thus to show that the supremum of ![]() $\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathcal {X}_{1}\times \mathcal {X}_{2}}})$ over all continuous volume-normalized metrics coincides with the supremum restricted to those which have positive curvature current and are product metrics. First, as shown in the proof of Theorem 2.5 we may restrict to those with positive curvature current. To prove that we may restrict to product metrics first consider the case when
$\widehat {\mathrm {vol}}_{\chi }(\overline {-\mathcal {K}_{\mathcal {X}_{1}\times \mathcal {X}_{2}}})$ over all continuous volume-normalized metrics coincides with the supremum restricted to those which have positive curvature current and are product metrics. First, as shown in the proof of Theorem 2.5 we may restrict to those with positive curvature current. To prove that we may restrict to product metrics first consider the case when ![]() $(X_{i},-K_{X_{i}})$ are both K-polystable. They thus admit Kähler–Einstein metrics and the corresponding product metric is Kähler–Einstein on
$(X_{i},-K_{X_{i}})$ are both K-polystable. They thus admit Kähler–Einstein metrics and the corresponding product metric is Kähler–Einstein on ![]() $X_{1}\times X_{2}$ and, as a consequence, realizes the supremum of
$X_{1}\times X_{2}$ and, as a consequence, realizes the supremum of ![]() $(\overline {-\mathcal {K}_{\mathcal {X}_{1}\times \mathcal {X}_{2}}})^{n+1},$ by Theorem 2.5 (strictly speaking, in the singular case the Kähler–Einstein metric is merely known to be locally bounded, but it can, in a standard way, be approximated by continuous ones). Finally, in the case when
$(\overline {-\mathcal {K}_{\mathcal {X}_{1}\times \mathcal {X}_{2}}})^{n+1},$ by Theorem 2.5 (strictly speaking, in the singular case the Kähler–Einstein metric is merely known to be locally bounded, but it can, in a standard way, be approximated by continuous ones). Finally, in the case when ![]() $(X_{i},-K_{X_{i}})$ are merely K-semistable we will use the following general observation. If
$(X_{i},-K_{X_{i}})$ are merely K-semistable we will use the following general observation. If ![]() $X_{1}$ and
$X_{1}$ and ![]() $X_{2}$ are K-semistable Fano varieties over
$X_{2}$ are K-semistable Fano varieties over ![]() $\mathbb {C},$ then the infimum of the Ding functional (formula (2.9)) corresponding to
$\mathbb {C},$ then the infimum of the Ding functional (formula (2.9)) corresponding to ![]() $X_{1}\times X_{2}$ coincides with the infimum over product metrics. To prove this, first recall the definition of the twisted Ding normalized functional
$X_{1}\times X_{2}$ coincides with the infimum over product metrics. To prove this, first recall the definition of the twisted Ding normalized functional ![]() $\mathcal {\hat {D}}_{\psi _{0},\gamma }$ corresponding to a given locally bounded psh metric
$\mathcal {\hat {D}}_{\psi _{0},\gamma }$ corresponding to a given locally bounded psh metric ![]() $\psi _{0}$ and
$\psi _{0}$ and ![]() $\gamma \in\, ]0,1]$:
$\gamma \in\, ]0,1]$:
By Hölder's inequality ![]() $\mathcal {\hat {D}}_{\psi _{0},\gamma }(\psi )$ is decreasing in
$\mathcal {\hat {D}}_{\psi _{0},\gamma }(\psi )$ is decreasing in ![]() $\gamma$. Since, as shown in the proof of Theorem 2.5,
$\gamma$. Since, as shown in the proof of Theorem 2.5, ![]() $\mathcal {\hat {D}}_{\psi _{0},1}$ is bounded from below when
$\mathcal {\hat {D}}_{\psi _{0},1}$ is bounded from below when ![]() $X\!$ is K-semistable, so is
$X\!$ is K-semistable, so is ![]() $\mathcal {\hat {D}}_{\psi _{0},\gamma }(\psi )$ for any
$\mathcal {\hat {D}}_{\psi _{0},\gamma }(\psi )$ for any ![]() $\gamma \in ]0,1[$. More precisely,
$\gamma \in ]0,1[$. More precisely, ![]() $\mathcal {\hat {D}}_{\psi _{0},\gamma }(\psi )$ is coercive for any given
$\mathcal {\hat {D}}_{\psi _{0},\gamma }(\psi )$ is coercive for any given ![]() $\gamma \in \,]0,1[$ (see the proof of [Reference BermanBer13, Corollary 3.6]) and thus
$\gamma \in \,]0,1[$ (see the proof of [Reference BermanBer13, Corollary 3.6]) and thus ![]() $\mathcal {\hat {D}}_{\psi _{0},\gamma }$ admits a minimizer
$\mathcal {\hat {D}}_{\psi _{0},\gamma }$ admits a minimizer ![]() $\psi _{\gamma }$ and the minimizers are precisely the solutions to the twisted Kähler–Einstein equation
$\psi _{\gamma }$ and the minimizers are precisely the solutions to the twisted Kähler–Einstein equation
(see [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19]). Thus, given two K-semistable Fano varieties ![]() $X_{1}$ and
$X_{1}$ and ![]() $X_{2}$ and
$X_{2}$ and ![]() $\gamma \in ]0,1[$, we may take two twisted Kähler–Einstein metrics
$\gamma \in ]0,1[$, we may take two twisted Kähler–Einstein metrics ![]() $\psi _{\gamma }^{(1)}$ and
$\psi _{\gamma }^{(1)}$ and ![]() $\psi _{\gamma }^{(2)}$ on
$\psi _{\gamma }^{(2)}$ on ![]() $-K_{X_{1}}$ and
$-K_{X_{1}}$ and ![]() $-K_{X_{2}}$, respectively. The corresponding product metric
$-K_{X_{2}}$, respectively. The corresponding product metric ![]() $\psi _{\gamma }$ on
$\psi _{\gamma }$ on ![]() $-K_{X_{1}\times X_{2}}$ is a twisted Kähler–Einstein metric and thus minimizes the twisted normalized Ding functional
$-K_{X_{1}\times X_{2}}$ is a twisted Kähler–Einstein metric and thus minimizes the twisted normalized Ding functional ![]() $\mathcal {\hat {D}}_{\psi _{0},\gamma }$ on
$\mathcal {\hat {D}}_{\psi _{0},\gamma }$ on ![]() $X_{1}\times X_{2}$. Moreover, as
$X_{1}\times X_{2}$. Moreover, as ![]() $\gamma \rightarrow 1$,
$\gamma \rightarrow 1$,
Indeed, ![]() $\gamma \rightarrow \mathcal {\hat {D}}_{\psi _{0},\gamma }(\psi )$ is continuous and concave on
$\gamma \rightarrow \mathcal {\hat {D}}_{\psi _{0},\gamma }(\psi )$ is continuous and concave on ![]() $]0,1]$ for a fixed continuous metric
$]0,1]$ for a fixed continuous metric ![]() $\psi,$ by Hölder's inequality. The convergence (2.23) thus follows from Lemma 2.11 below. Finally, since in our setup
$\psi,$ by Hölder's inequality. The convergence (2.23) thus follows from Lemma 2.11 below. Finally, since in our setup ![]() $\psi _{\gamma }$ is a product metric it follows that the infimum of
$\psi _{\gamma }$ is a product metric it follows that the infimum of ![]() $\mathcal {\hat {D}}_{\psi _{0}}$ coincides with the infimum restricted to product metrics, as desired.
$\mathcal {\hat {D}}_{\psi _{0}}$ coincides with the infimum restricted to product metrics, as desired.
In the proof we used the following elementary result about convex functions (applied to ![]() $-f)$.
$-f)$.
Lemma 2.11 Let ![]() $f(t)$ be a function
$f(t)$ be a function ![]() $[0,1]\rightarrow \,]{-}\infty,\infty ]$ of the form
$[0,1]\rightarrow \,]{-}\infty,\infty ]$ of the form
where ![]() $f_{p}(t)$ is a family of continuous convex functions on
$f_{p}(t)$ is a family of continuous convex functions on ![]() $[0,1],$ parametrized by a set
$[0,1],$ parametrized by a set ![]() $\mathcal {P}$. Then
$\mathcal {P}$. Then ![]() $f(t)$ is continuous on
$f(t)$ is continuous on ![]() $[0,1]$.
$[0,1]$.
Proof. This is standard, but for completeness we provide a proof. Recall that the supremum of a family of continuous functions is lower semicontinuous. Hence, it will be enough to show that ![]() $f(t)$ is upper semicontinuous. To this end, observe that since
$f(t)$ is upper semicontinuous. To this end, observe that since ![]() $t\mapsto f_{p}(t)$ is convex it follows that
$t\mapsto f_{p}(t)$ is convex it follows that ![]() $f(t)$ is also convex. But any convex function on
$f(t)$ is also convex. But any convex function on ![]() $[0,1]$ is upper semicontinuous. Indeed,
$[0,1]$ is upper semicontinuous. Indeed, ![]() $f$ is (Lipschitz) continuous on
$f$ is (Lipschitz) continuous on ![]() $]0,1[\, ,$ since it is convex there. By symmetry, it is thus enough to prove upper continuity at
$]0,1[\, ,$ since it is convex there. By symmetry, it is thus enough to prove upper continuity at ![]() $t=1$. Now, since
$t=1$. Now, since ![]() $f(t)$ is convex we have, given
$f(t)$ is convex we have, given ![]() $t\in ]0,1[,$ that
$t\in ]0,1[,$ that
for any subgradient ![]() $\partial f(t)$ at
$\partial f(t)$ at ![]() $t,$ i.e. any one-sided derivative at
$t,$ i.e. any one-sided derivative at ![]() $t$. But since
$t$. But since ![]() $f(t)$ is convex,
$f(t)$ is convex, ![]() $\partial f(t)\geq \partial f(t_{0})$ for any fixed
$\partial f(t)\geq \partial f(t_{0})$ for any fixed ![]() $t_{0}$ such that
$t_{0}$ such that ![]() $t_{0}\leq t$. Hence,
$t_{0}\leq t$. Hence, ![]() $f(1)\geq f(t)+(1-t)\partial f(t_{0})$ and letting
$f(1)\geq f(t)+(1-t)\partial f(t_{0})$ and letting ![]() $t\rightarrow 1$ thus shows that
$t\rightarrow 1$ thus shows that ![]() $f(1)$ is greater than or equal to the limit supremum of
$f(1)$ is greater than or equal to the limit supremum of ![]() $f(t)$ as
$f(t)$ as ![]() $t\rightarrow 1,$ as desired.
$t\rightarrow 1,$ as desired.
3. Sharp height inequalities in the toric case
We now specialize to the case when ![]() $X\!$ is a toric Fano variety.
$X\!$ is a toric Fano variety.
3.1 The toric setup
We start by recalling the notation for toric metrics employed in [Reference Berman and BerndtssonBB13] and the relation to the canonical toric integral model.
3.1.1 The moment polytope  $P(L)$
$P(L)$
Let ![]() $X\!$ be an
$X\!$ be an ![]() $n$-dimensional complex projective toric variety, i.e. a complex projective variety endowed with an action of the
$n$-dimensional complex projective toric variety, i.e. a complex projective variety endowed with an action of the ![]() $n$-dimensional complex torus
$n$-dimensional complex torus ![]() $\mathbb {C}^{*n}$ with an open dense orbit. We shall denote by
$\mathbb {C}^{*n}$ with an open dense orbit. We shall denote by ![]() $T_{c}$ the complex torus and by
$T_{c}$ the complex torus and by ![]() $T$ the real maximal compact subtorus of
$T$ the real maximal compact subtorus of ![]() $T_{c},$ i.e.
$T_{c},$ i.e. ![]() $T=(S^{1})^{n}$. Let
$T=(S^{1})^{n}$. Let ![]() $L$ be a toric ample line bundle, i.e. an ample line bundle over
$L$ be a toric ample line bundle, i.e. an ample line bundle over ![]() $X\!$ endowed with a
$X\!$ endowed with a ![]() $T_{c}$-action covering the action of
$T_{c}$-action covering the action of ![]() $T_{c}$ on
$T_{c}$ on ![]() $X$. It induces a bounded convex polytope
$X$. It induces a bounded convex polytope ![]() $P(L)$ in
$P(L)$ in ![]() $\mathbb {R}^{d}$ with non-empty interior, defined as follows. Consider the induced action of the group
$\mathbb {R}^{d}$ with non-empty interior, defined as follows. Consider the induced action of the group ![]() $T_{c}$ on the space
$T_{c}$ on the space ![]() $H^{0}(X,kL)$ of global holomorphic sections of
$H^{0}(X,kL)$ of global holomorphic sections of ![]() $kL\rightarrow X$ (for
$kL\rightarrow X$ (for ![]() $k$ a given positive integer). Decomposing the action of
$k$ a given positive integer). Decomposing the action of ![]() $T_{c}$ according to the corresponding one-dimensional representations
$T_{c}$ according to the corresponding one-dimensional representations ![]() $e^{m},$ labeled by
$e^{m},$ labeled by ![]() $m\in \mathbb {Z}^{n}$,
$m\in \mathbb {Z}^{n}$,
the lattice polytope ![]() $P_{(X,L)}$ may be defined as the convex hull of
$P_{(X,L)}$ may be defined as the convex hull of ![]() $k^{-1}B_{k}$ in
$k^{-1}B_{k}$ in ![]() $\mathbb {R}^{n}$, for
$\mathbb {R}^{n}$, for ![]() $k$ sufficiently large. More generally, by homogeneity,
$k$ sufficiently large. More generally, by homogeneity, ![]() $P_{(X,L)}$ is defined for any ample
$P_{(X,L)}$ is defined for any ample ![]() $\mathbb {Q}$-line bundle.
$\mathbb {Q}$-line bundle.
In particular, if ![]() $X\!$ is Fano, then the polytope
$X\!$ is Fano, then the polytope ![]() $P(-K_{X}\!)$ has vertices in
$P(-K_{X}\!)$ has vertices in ![]() $\mathbb {Q}^{n}$ and may be represented as follows:
$\mathbb {Q}^{n}$ and may be represented as follows:
where ![]() $F$ ranges over all facets of
$F$ ranges over all facets of ![]() $P(-K_{X}\!)$ and
$P(-K_{X}\!)$ and ![]() $l_{F}$ denotes the unique primitive element in
$l_{F}$ denotes the unique primitive element in ![]() $\mathbb {Z}^{n}$ which is an interior normal to the facet
$\mathbb {Z}^{n}$ which is an interior normal to the facet ![]() $F$ (i.e.
$F$ (i.e. ![]() $P(-K_{X}\!)$ is the dual of the polytope with primitive vertices
$P(-K_{X}\!)$ is the dual of the polytope with primitive vertices ![]() $l_{F})$. Conversely, any such polytope corresponds to a Fano variety
$l_{F})$. Conversely, any such polytope corresponds to a Fano variety ![]() $X\!$ [Reference Cox, Little and SchenckCLS11, Reference Berman and BerndtssonBB13].
$X\!$ [Reference Cox, Little and SchenckCLS11, Reference Berman and BerndtssonBB13].
Example 3.1 When ![]() $X=\mathbb {P}^{n}$ the polytope
$X=\mathbb {P}^{n}$ the polytope ![]() $P(-K_{X}\!)$ is
$P(-K_{X}\!)$ is ![]() $(n+1)(\Sigma _{n}-(1,\ldots,1))$ where
$(n+1)(\Sigma _{n}-(1,\ldots,1))$ where ![]() $\Sigma _{n}$ denotes the
$\Sigma _{n}$ denotes the ![]() $n$-dimensional unit simplex. An infinite family of two-dimensional toric Fano varieties
$n$-dimensional unit simplex. An infinite family of two-dimensional toric Fano varieties ![]() $X_{p,q},$ parametrized by two prime numbers
$X_{p,q},$ parametrized by two prime numbers ![]() $p$ and
$p$ and ![]() $q,$ is obtained by letting
$q,$ is obtained by letting ![]() $P(-K_{X_{p,q}})$ be the polytope which is dual to the polytope with the four primitive vertices
$P(-K_{X_{p,q}})$ be the polytope which is dual to the polytope with the four primitive vertices ![]() $(\pm p,\pm q)$. In particular,
$(\pm p,\pm q)$. In particular, ![]() $\mathrm {vol}{(-K_{X_{p,q}})}=2/(pq)$ tends to zero when
$\mathrm {vol}{(-K_{X_{p,q}})}=2/(pq)$ tends to zero when ![]() $pq$ tends to infinity.
$pq$ tends to infinity.
Remark 3.2 From an invariant point of view, the real vector space ![]() $\mathbb {R}^{n}$ above arises as
$\mathbb {R}^{n}$ above arises as ![]() $M\otimes _{\mathbb {Z}}\mathbb {R},$ where
$M\otimes _{\mathbb {Z}}\mathbb {R},$ where ![]() $M$ is the lattice
$M$ is the lattice ![]() $\mathrm {Hom}{(T_{c},\mathbb {C}^{*})}$ of characters of the group
$\mathrm {Hom}{(T_{c},\mathbb {C}^{*})}$ of characters of the group ![]() $T_{c}$ (cf. [Reference Cox, Little and SchenckCLS11]).
$T_{c}$ (cf. [Reference Cox, Little and SchenckCLS11]).
3.1.2 Logarithmic coordinates and the Legendre transform  $\phi ^{*}$ of a metric
$\phi ^{*}$ of a metric  $\phi$ on
$\phi$ on  $L$
$L$
Since ![]() $X\!$ is toric we can identify
$X\!$ is toric we can identify ![]() $T_{c}$ with its open orbit in
$T_{c}$ with its open orbit in ![]() $X$. Let
$X$. Let ![]() $\mbox {Log}$ be the map from
$\mbox {Log}$ be the map from ![]() $T_{c}$ to
$T_{c}$ to ![]() $\mathbb {R}^{n}$ defined by
$\mathbb {R}^{n}$ defined by
The real compact torus ![]() $T$ acts transitively on its fibers. We will refer to
$T$ acts transitively on its fibers. We will refer to ![]() $x$ as the (real) logarithmic coordinates on
$x$ as the (real) logarithmic coordinates on ![]() $T_{c}$. Let
$T_{c}$. Let ![]() $L$ be a toric ample line bundle over
$L$ be a toric ample line bundle over ![]() $X\!$ and assume that
$X\!$ and assume that ![]() $P$ contains the origin,
$P$ contains the origin, ![]() $0\in P,$ and denote by
$0\in P,$ and denote by ![]() $e^{0}$ the corresponding
$e^{0}$ the corresponding ![]() $T$-invariant element in
$T$-invariant element in ![]() $H^{0}(X,kL)$. Any continuous
$H^{0}(X,kL)$. Any continuous ![]() $T$-invariant metric
$T$-invariant metric ![]() $\Vert \cdot \Vert$ on
$\Vert \cdot \Vert$ on ![]() $L$ induces a continuous function on
$L$ induces a continuous function on ![]() $\mathbb {R}^{n}$ which we shall denote by
$\mathbb {R}^{n}$ which we shall denote by ![]() $\phi (x)$, defined as
$\phi (x)$, defined as
Thus, in the present additive notation ![]() $\phi$ for metrics we have
$\phi$ for metrics we have ![]() $\phi (x)=\phi _{U}(z),$ when
$\phi (x)=\phi _{U}(z),$ when ![]() $U=T_{c},$ abusing notation slightly. The Legendre transform of
$U=T_{c},$ abusing notation slightly. The Legendre transform of ![]() $\phi (x),$ which defines a lower-semicontinuous convex function on
$\phi (x),$ which defines a lower-semicontinuous convex function on ![]() $\mathbb {R}^{n}$ (taking values in
$\mathbb {R}^{n}$ (taking values in ![]() $]{-}\infty,\infty ])$ will be denoted by
$]{-}\infty,\infty ])$ will be denoted by ![]() $\phi ^{*}$:
$\phi ^{*}$:
A ![]() $T$-invariant continuous metric
$T$-invariant continuous metric ![]() $\psi$ on
$\psi$ on ![]() $L$ is psh if and only if the corresponding function
$L$ is psh if and only if the corresponding function ![]() $\psi (x)$ on
$\psi (x)$ on ![]() $\mathbb {R}^{n}$ is convex (if and only if
$\mathbb {R}^{n}$ is convex (if and only if ![]() $\psi (x)=\psi ^{**}(x))$. We will denote by
$\psi (x)=\psi ^{**}(x))$. We will denote by ![]() $\psi _{P(L)}$ the unique continuous convex function on
$\psi _{P(L)}$ the unique continuous convex function on ![]() $\mathbb {R}^{n}$ whose Legendre transform is equal to
$\mathbb {R}^{n}$ whose Legendre transform is equal to ![]() $0$ on
$0$ on ![]() $P(L)$ and equal to
$P(L)$ and equal to ![]() $\infty$ on the complement of
$\infty$ on the complement of ![]() $P(L)$:
$P(L)$:
It corresponds to a continuous psh metric on ![]() $L$ (see the proof of [Reference Berman and BerndtssonBB13, Proposition 3.3]) and it will be used as a canonical reference metric in the present toric setup. It follows that for any other continuous metric
$L$ (see the proof of [Reference Berman and BerndtssonBB13, Proposition 3.3]) and it will be used as a canonical reference metric in the present toric setup. It follows that for any other continuous metric ![]() $\phi$ on
$\phi$ on ![]() $L$,
$L$,
Remark 3.3 From an invariant point of view the logarithm coordinates take values in ![]() $N\otimes \mathbb {R},$ where
$N\otimes \mathbb {R},$ where ![]() $N$ is the lattice
$N$ is the lattice ![]() $\mathrm {Hom}{(\mathbb {C}^{*},T_{c})}$ of one-parameter subgroups of
$\mathrm {Hom}{(\mathbb {C}^{*},T_{c})}$ of one-parameter subgroups of ![]() $T_{c},$ i.e. the dual of the lattice
$T_{c},$ i.e. the dual of the lattice ![]() $\mathrm {Hom}{(T_{c},\mathbb {C}^{*})}$ of characters of
$\mathrm {Hom}{(T_{c},\mathbb {C}^{*})}$ of characters of ![]() $T_{c}$.
$T_{c}$.
3.1.3 Pushing forward measures from  $X\!$ to
$X\!$ to  $\mathbb {R}^{n}$
$\mathbb {R}^{n}$
For any ![]() $T$-invariant continuous psh metric
$T$-invariant continuous psh metric ![]() $\psi$ on
$\psi$ on ![]() $L$ the push-forward of the measure
$L$ the push-forward of the measure ![]() $(dd^{c}\psi )^{n}/n!$ on
$(dd^{c}\psi )^{n}/n!$ on ![]() $L$ under the map
$L$ under the map ![]() $\mbox {Log}$ is given by
$\mbox {Log}$ is given by
(since the integral along the ![]() $T^{n}$-fibers equals
$T^{n}$-fibers equals ![]() $(2\pi )^{n})$. The measure on the right-hand side is defined in the weak sense of Alexandrov. Since the closure of the image of
$(2\pi )^{n})$. The measure on the right-hand side is defined in the weak sense of Alexandrov. Since the closure of the image of ![]() $\mathbb {R}^{n}$ under the subgradient map of
$\mathbb {R}^{n}$ under the subgradient map of ![]() $\phi$ equals
$\phi$ equals ![]() $P$ it follows that
$P$ it follows that
where ![]() $dy$ is Lebesgue measure. Next consider the case when
$dy$ is Lebesgue measure. Next consider the case when ![]() $L=-K_{X}$. Then
$L=-K_{X}$. Then
defines a ![]() $T_{c}$-invariant global holomorphic section of
$T_{c}$-invariant global holomorphic section of ![]() $-K_{X},$ trivializing
$-K_{X},$ trivializing ![]() $-K_{X\!}$ over
$-K_{X\!}$ over ![]() $U:=\mathbb {C}^{*n}$. We can thus identify a continuous metric
$U:=\mathbb {C}^{*n}$. We can thus identify a continuous metric ![]() $\phi$ on
$\phi$ on ![]() $-K_{X\!}$ with the corresponding function
$-K_{X\!}$ with the corresponding function ![]() $\phi _{U}$ on
$\phi _{U}$ on ![]() $\mathbb {C}^{*n}$ (formula (2.1)) and volume form on
$\mathbb {C}^{*n}$ (formula (2.1)) and volume form on ![]() $X\!$ (formula (2.3)) expressed as follows on
$X\!$ (formula (2.3)) expressed as follows on ![]() $\mathbb {C}^{*n},$ with respect to the local holomorphic coordinate
$\mathbb {C}^{*n},$ with respect to the local holomorphic coordinate ![]() $\log z$:
$\log z$:
symbolically denoted by ![]() $e^{-\phi }$. Using again that the integral along the
$e^{-\phi }$. Using again that the integral along the ![]() $T^{n}$-fibers equals
$T^{n}$-fibers equals ![]() $(2\pi )^{n}$ yields
$(2\pi )^{n}$ yields
3.1.4 K-semistability and toric Kähler–Einstein metrics
We recall the following result, which is a combination of [Reference Berman and BerndtssonBB13, Theorem 1.2] and [Reference BermanBer16, Corollary 1.2] (which are formulated in terms of ![]() $T_{c}$-equivariant K-polystability and K-polystability, respectively).
$T_{c}$-equivariant K-polystability and K-polystability, respectively).
Proposition 3.4 Let ![]() $X\!$ be a toric Fano variety. The following statements are equivalent.
$X\!$ be a toric Fano variety. The following statements are equivalent.
•
 $X\!$ is K-semistable.
$X\!$ is K-semistable.•
 $X\!$ is K-polystable.
$X\!$ is K-polystable.•
 $X\!$ admits a
$X\!$ admits a  $T$-invariant Kähler–Einstein metric.
$T$-invariant Kähler–Einstein metric.• The barycenter of
 $P(-K_{X}\!)$ coincides with the origin
$P(-K_{X}\!)$ coincides with the origin  $0$.
$0$.
3.1.5 The arithmetic  $\chi$-volume of a toric metric
$\chi$-volume of a toric metric
Any toric ample line bundle ![]() $L\rightarrow X$ admits a canonical integral model
$L\rightarrow X$ admits a canonical integral model ![]() $\mathcal {L}\rightarrow \mathcal {X}$ over
$\mathcal {L}\rightarrow \mathcal {X}$ over ![]() $\mathbb {Z}$ with
$\mathbb {Z}$ with ![]() $\mathcal {X}$ normal (see [Reference MaillotMai00, § 2] and [Reference Burgos Gil, Philippon and SombraBPS14, Def 3.5.6]).
$\mathcal {X}$ normal (see [Reference MaillotMai00, § 2] and [Reference Burgos Gil, Philippon and SombraBPS14, Def 3.5.6]).
The following result is a special case of the main result of [Reference Burgos Gil, Philippon and SombraBPS14, Theorem 3] (combined with Lemma 2.8):
Proposition 3.5 Let ![]() $L\rightarrow X$ be an ample toric line bundle and denote by
$L\rightarrow X$ be an ample toric line bundle and denote by ![]() $(\mathcal {X},\mathcal {L})$ its canonical toric model over
$(\mathcal {X},\mathcal {L})$ its canonical toric model over ![]() $\mathbb {Z}$. Assume that
$\mathbb {Z}$. Assume that ![]() $\phi$ is a continuous
$\phi$ is a continuous ![]() $T$-invariant metric on
$T$-invariant metric on ![]() $L$. Then
$L$. Then
An alternative analytic proof of this formula can also be given, using that the integral lattice ![]() $H^{0}(\mathcal {X},k\mathcal {L})$ in
$H^{0}(\mathcal {X},k\mathcal {L})$ in ![]() $H^{0}(X,kL)$ is generated by the
$H^{0}(X,kL)$ is generated by the ![]() $T_{c}$-equivariant bases
$T_{c}$-equivariant bases ![]() $e^{m}$ appearing in the decomposition (3.1) [Reference MaillotMai00]. Since this basis is orthonormal with respect to the
$e^{m}$ appearing in the decomposition (3.1) [Reference MaillotMai00]. Since this basis is orthonormal with respect to the ![]() $L^{2}$-norm on
$L^{2}$-norm on ![]() $H^{0}(X,kL)$ induced by the metric
$H^{0}(X,kL)$ induced by the metric ![]() $\psi _{P(L)}$ on
$\psi _{P(L)}$ on ![]() $L,$ defined by formula (3.3) and the Haar measure on the unit torus
$L,$ defined by formula (3.3) and the Haar measure on the unit torus ![]() $T\Subset X,$ applying [Reference Berman and BoucksomBB10, Theorem A] yields
$T\Subset X,$ applying [Reference Berman and BoucksomBB10, Theorem A] yields
When ![]() $\phi$ is toric the right-hand side above coincides, by [Reference Berman and BerndtssonBB13, Proposition 2.9], with the right-hand side of the formula in the previous proposition.
$\phi$ is toric the right-hand side above coincides, by [Reference Berman and BerndtssonBB13, Proposition 2.9], with the right-hand side of the formula in the previous proposition.
3.1.6 Arithmetic toric Fano varieties
Now assume that ![]() $X\!$ is a toric Fano variety, so that
$X\!$ is a toric Fano variety, so that ![]() $-K_{X\!}$ defines an ample
$-K_{X\!}$ defines an ample ![]() $\mathbb {Q}$-line bundle. Then the canonical integral model
$\mathbb {Q}$-line bundle. Then the canonical integral model ![]() $\mathcal {X}$ of
$\mathcal {X}$ of ![]() $X\!$ over
$X\!$ over ![]() $\mathbb {Z}$ is a normal arithmetic Fano variety, i.e. the relative anti-canonical divisor
$\mathbb {Z}$ is a normal arithmetic Fano variety, i.e. the relative anti-canonical divisor ![]() $-\mathcal {K}$ on
$-\mathcal {K}$ on ![]() $\mathcal {X}$ defines a relatively ample
$\mathcal {X}$ defines a relatively ample ![]() $\mathbb {Q}$-line bundle on
$\mathbb {Q}$-line bundle on ![]() $\mathcal {X}$. Indeed,
$\mathcal {X}$. Indeed, ![]() $-\mathcal {K}$ coincides with the canonical integral model
$-\mathcal {K}$ coincides with the canonical integral model ![]() $\mathcal {L}$ of
$\mathcal {L}$ of ![]() $-K_{X}$. This follows (just as in the function field case considered in [Reference BermanBer16, Lemma 2.2]) from the fact that the fibers of the structure morphism
$-K_{X}$. This follows (just as in the function field case considered in [Reference BermanBer16, Lemma 2.2]) from the fact that the fibers of the structure morphism ![]() $\mathcal {X}\rightarrow \mathrm {Spec}{\mathbb {Z}}$ are reduced and irreducible.
$\mathcal {X}\rightarrow \mathrm {Spec}{\mathbb {Z}}$ are reduced and irreducible.
3.2 Proof of Theorem 1.2
Given a Fano variety ![]() $X,$ let
$X,$ let ![]() $\phi$ be a continuous metric on
$\phi$ be a continuous metric on ![]() $-K_{X\!}$ which is volume-normalized. We will prove the following more general formulation of the inequality in Theorem 1.2 (where the psh assumption on
$-K_{X\!}$ which is volume-normalized. We will prove the following more general formulation of the inequality in Theorem 1.2 (where the psh assumption on ![]() $\phi$ has been dispensed with):
$\phi$ has been dispensed with):
where the metric on ![]() $-K_{\mathbb {P}^{n}}$ is the one induced by the volume-normalized Fubini–Study metric.
$-K_{\mathbb {P}^{n}}$ is the one induced by the volume-normalized Fubini–Study metric.
A ![]() $T$-invariant continuous metric
$T$-invariant continuous metric ![]() $\phi$ will, as above, be identified with a function
$\phi$ will, as above, be identified with a function ![]() $\phi (x)$ on
$\phi (x)$ on ![]() $\mathbb {R}^{n}$. Moreover, if
$\mathbb {R}^{n}$. Moreover, if ![]() $\phi$ is volume-normalized then Proposition 3.5 gives
$\phi$ is volume-normalized then Proposition 3.5 gives
 \begin{align} 2\widehat{\mathrm{vol}}_{\chi}(\mathcal{-}\mathcal{K},\phi)/\mathrm{vol}(-K_{X}) &=-\mathcal{\hat{D}}_{\mathbb{Z}}(\phi)=-\mathcal{\hat{D}}_{\psi_{P}}(\phi)\nonumber\\ &= -\int_{P}\phi^{*}\,dy/\mathrm{vol}(-K_{X}\!)+\log\int_{\mathbb{R}^{n}}e^{-\phi(x)}\,dx +n\log\pi, \end{align}
\begin{align} 2\widehat{\mathrm{vol}}_{\chi}(\mathcal{-}\mathcal{K},\phi)/\mathrm{vol}(-K_{X}) &=-\mathcal{\hat{D}}_{\mathbb{Z}}(\phi)=-\mathcal{\hat{D}}_{\psi_{P}}(\phi)\nonumber\\ &= -\int_{P}\phi^{*}\,dy/\mathrm{vol}(-K_{X}\!)+\log\int_{\mathbb{R}^{n}}e^{-\phi(x)}\,dx +n\log\pi, \end{align}
where ![]() $\mathcal {\hat {D}}_{\mathbb {Z}}(\phi )$ and
$\mathcal {\hat {D}}_{\mathbb {Z}}(\phi )$ and ![]() $\mathcal {\hat {D}}_{\psi _{P}}(\phi )$ are the Ding type functionals defined by formula (2.15) and formula (2.16), respectively, and we have used formula (3.6).
$\mathcal {\hat {D}}_{\psi _{P}}(\phi )$ are the Ding type functionals defined by formula (2.15) and formula (2.16), respectively, and we have used formula (3.6).
We start by recording the following explicit formula for the arithmetic volume of projective space ![]() $\mathbb {P}^{n}$, endowed with a volume-normalized Kähler–Einstein metric (which may be assumed to be the metric induced by the Fubini–Study metric).
$\mathbb {P}^{n}$, endowed with a volume-normalized Kähler–Einstein metric (which may be assumed to be the metric induced by the Fubini–Study metric).
Lemma 3.6 The following formulas hold for the metrics ![]() $\phi _{\mathrm {KE}}$ on the anti-canonical line bundles of
$\phi _{\mathrm {KE}}$ on the anti-canonical line bundles of ![]() $\mathbb {P}_{\mathbb {C}}^{n}$ induced by a volume-normalized toric Kähler–Einstein metric:
$\mathbb {P}_{\mathbb {C}}^{n}$ induced by a volume-normalized toric Kähler–Einstein metric:
 \[ X=\mathbb{P}_{\mathbb{C}}^{n}\implies2\widehat{\mathrm{vol}}_{\chi}(\mathcal{-K},\phi_{\mathrm{KE}})=\frac{(n+1)^{n}}{n!}\Biggl((n+1)\sum_{k=1}^{n}k^{-1}-n+\log\biggl(\frac{\pi^{n}}{n!}\biggr)\Biggr)>0. \]
\[ X=\mathbb{P}_{\mathbb{C}}^{n}\implies2\widehat{\mathrm{vol}}_{\chi}(\mathcal{-K},\phi_{\mathrm{KE}})=\frac{(n+1)^{n}}{n!}\Biggl((n+1)\sum_{k=1}^{n}k^{-1}-n+\log\biggl(\frac{\pi^{n}}{n!}\biggr)\Biggr)>0. \]
Proof. Consider the case when ![]() $X=\mathbb {P}_{\mathbb {C}}^{n},$ whose canonical integral model is given by
$X=\mathbb {P}_{\mathbb {C}}^{n},$ whose canonical integral model is given by ![]() $\mathcal {X}=\mathbb {P}_{\mathbb {Z}}^{n}$. The canonical model of the anti-canonical line bundle of
$\mathcal {X}=\mathbb {P}_{\mathbb {Z}}^{n}$. The canonical model of the anti-canonical line bundle of ![]() $\mathbb {P}_{\mathbb {C}}^{n}$ is given by
$\mathbb {P}_{\mathbb {C}}^{n}$ is given by ![]() $\mathcal {O}(1)^{\otimes n+1}\rightarrow \mathbb {P}_{\mathbb {Z}}^{n}$. As shown in [Reference Gillet and SouléGS90, § 5.4] (using the induction formula for the height; see also [Reference SouléSou21, Proposition 3.10]) the height
$\mathcal {O}(1)^{\otimes n+1}\rightarrow \mathbb {P}_{\mathbb {Z}}^{n}$. As shown in [Reference Gillet and SouléGS90, § 5.4] (using the induction formula for the height; see also [Reference SouléSou21, Proposition 3.10]) the height ![]() $h_{\mathrm {FS}}$ of
$h_{\mathrm {FS}}$ of ![]() $\mathcal {O}(1)\rightarrow \mathbb {P}_{\mathbb {Z}}^{n}$ endowed with the Fubini–Study metric
$\mathcal {O}(1)\rightarrow \mathbb {P}_{\mathbb {Z}}^{n}$ endowed with the Fubini–Study metric ![]() $\phi _{\mathrm {FS}}$ is given by
$\phi _{\mathrm {FS}}$ is given by
 \[ h_{\mathrm{FS}}=\frac{1}{2}\sum_{k=1}^{n}\sum_{m=1}^{k}m^{-1}. \]
\[ h_{\mathrm{FS}}=\frac{1}{2}\sum_{k=1}^{n}\sum_{m=1}^{k}m^{-1}. \]
Since ![]() $(n+1)\phi _{\mathrm {FS}}$ defines a Kähler–Einstein metric on
$(n+1)\phi _{\mathrm {FS}}$ defines a Kähler–Einstein metric on ![]() $-K_{\mathbb {P}^{n}}$ and
$-K_{\mathbb {P}^{n}}$ and ![]() $\pi ^{-n}\int _{\mathbb {P}^{n}}e^{-(n+1)\phi _{\mathrm {FS}}}=1/n!$ this gives
$\pi ^{-n}\int _{\mathbb {P}^{n}}e^{-(n+1)\phi _{\mathrm {FS}}}=1/n!$ this gives
 \begin{align*} 2\widehat{\mathrm{vol}}_{\chi}(-\mathcal{K},\phi_{\mathrm{KE}}) -n\log\pi&=(n+1)^{n+1}\frac{h_{\mathrm{FS}}}{(n+1)!}+\frac{(n+1)^{n}}{n!} \log\biggl(\frac{1}{n!}\biggr)\\ &=\frac{(n+1)^{n}}{n!}\biggl(h_{\mathrm{FS}}+\log\biggl(\frac{1}{n!}\biggr)\biggr), \end{align*}
\begin{align*} 2\widehat{\mathrm{vol}}_{\chi}(-\mathcal{K},\phi_{\mathrm{KE}}) -n\log\pi&=(n+1)^{n+1}\frac{h_{\mathrm{FS}}}{(n+1)!}+\frac{(n+1)^{n}}{n!} \log\biggl(\frac{1}{n!}\biggr)\\ &=\frac{(n+1)^{n}}{n!}\biggl(h_{\mathrm{FS}}+\log\biggl(\frac{1}{n!}\biggr)\biggr), \end{align*}
using formula (2.6) in the first term, combined with the homogeneity property (2.7) and, in the second term, the scaling property (2.8). Rewriting the formula for ![]() $h_{\mathrm {FS}}$ above as a triangle sum and changing the order of summation then concludes the proof of the formula of the lemma. The last positivity statement will be shown in the course of the proof of Lemma 3.8.
$h_{\mathrm {FS}}$ above as a triangle sum and changing the order of summation then concludes the proof of the formula of the lemma. The last positivity statement will be shown in the course of the proof of Lemma 3.8.
The key ingredient in the proof of Theorem 1.2 is the following universal bound on the arithmetic volume, in terms of the ordinary volume.
Proposition 3.7 For any ![]() $n$-dimensional toric Fano variety
$n$-dimensional toric Fano variety ![]() $X\!$ which is K-semistable, the following bound holds for any volume-normalized continuous metric
$X\!$ which is K-semistable, the following bound holds for any volume-normalized continuous metric ![]() $\phi$ on
$\phi$ on ![]() $-K_{X\!}$:
$-K_{X\!}$:
Proof. Recall that, as shown at the beginning of the proof of Theorem 2.5, it is equivalent to establish the upper bound for ![]() $-\mathcal {\hat {D}}_{\psi _{P}}(\phi )$ when
$-\mathcal {\hat {D}}_{\psi _{P}}(\phi )$ when ![]() $\phi$ is a continuous psh metric on
$\phi$ is a continuous psh metric on ![]() $L$. Since
$L$. Since ![]() $X\!$ is assumed K-semistable, it follows from Proposition 3.4 that
$X\!$ is assumed K-semistable, it follows from Proposition 3.4 that ![]() $X\!$ admits a
$X\!$ admits a ![]() $T$-invariant Kähler–Einstein metric. In general, a Kähler–Einstein metric
$T$-invariant Kähler–Einstein metric. In general, a Kähler–Einstein metric ![]() $\phi$ on
$\phi$ on ![]() $-K_{X\!}$ minimizes the normalized Ding functional
$-K_{X\!}$ minimizes the normalized Ding functional ![]() $\mathcal {\hat {D}}_{\psi _{0}}$ [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19]. Thus in the toric case the infimum of
$\mathcal {\hat {D}}_{\psi _{0}}$ [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19]. Thus in the toric case the infimum of ![]() $\mathcal {\hat {D}}_{\psi _{0}}$ coincides with the infimum over all continuous
$\mathcal {\hat {D}}_{\psi _{0}}$ coincides with the infimum over all continuous ![]() $T$-invariant psh metrics. As explained in § 3.1.2, such a metric may be identified with a convex function
$T$-invariant psh metrics. As explained in § 3.1.2, such a metric may be identified with a convex function ![]() $\phi (x)$ on
$\phi (x)$ on ![]() $\mathbb {R}^{n}$ satisfying
$\mathbb {R}^{n}$ satisfying ![]() $\phi -\psi _{P}\in L^{\infty }(\mathbb {R}^{n})$. By formula (3.8) it will be enough to show that for such convex functions
$\phi -\psi _{P}\in L^{\infty }(\mathbb {R}^{n})$. By formula (3.8) it will be enough to show that for such convex functions
Since ![]() $0$ is contained in the interior of
$0$ is contained in the interior of ![]() $P$ the measure
$P$ the measure ![]() $e^{-\phi }dx$ on
$e^{-\phi }dx$ on ![]() $\mathbb {R}^{n}$ has finite moments. Recall that by Proposition 3.4 the barycenter of
$\mathbb {R}^{n}$ has finite moments. Recall that by Proposition 3.4 the barycenter of ![]() $P$ coincides with
$P$ coincides with ![]() $0\in \mathbb {R}^{n}$ and, as a consequence, the left-hand side in inequality (3.9) is invariant under translations of
$0\in \mathbb {R}^{n}$ and, as a consequence, the left-hand side in inequality (3.9) is invariant under translations of ![]() $\phi$,
$\phi$, ![]() $\phi (x)\mapsto \phi (x+a)$ for any given
$\phi (x)\mapsto \phi (x+a)$ for any given ![]() $a\in \mathbb {R}^{n}$ [Reference Berman and BerndtssonBB13, Lemma 2.14]. As a consequence, in order to prove inequality (3.9) we may as well assume that
$a\in \mathbb {R}^{n}$ [Reference Berman and BerndtssonBB13, Lemma 2.14]. As a consequence, in order to prove inequality (3.9) we may as well assume that
By the functional form of Santaló's inequality [Reference Artstein, Klartag and MilmanAKM04, Lemma 2.14] this implies that
(where equality holds if ![]() $\phi =\phi ^{*}$, i.e. if
$\phi =\phi ^{*}$, i.e. if ![]() $\phi (x)=|x|^{2}/2)$. Moreover, by Jensen's inequality,
$\phi (x)=|x|^{2}/2)$. Moreover, by Jensen's inequality,
using in the last equality that ![]() $\phi ^{*}=\infty$ on the complement of
$\phi ^{*}=\infty$ on the complement of ![]() $P$ (see formula (3.4)). Combining the latter two inequalities yields the desired inequality (3.9).
$P$ (see formula (3.4)). Combining the latter two inequalities yields the desired inequality (3.9).
Recall that ![]() $\mathbb {P}^{n}$ has maximal volume among all K-semistable
$\mathbb {P}^{n}$ has maximal volume among all K-semistable ![]() $n$-dimensional Fano varieties (as shown in [Reference Berman and BerndtssonBB17] in the toric case and in [Reference FujitaFuj18] in general). We next show that it will be enough to prove that, in the toric case, the next to largest volume is attained by
$n$-dimensional Fano varieties (as shown in [Reference Berman and BerndtssonBB17] in the toric case and in [Reference FujitaFuj18] in general). We next show that it will be enough to prove that, in the toric case, the next to largest volume is attained by ![]() $\mathbb {P}^{n-1}\times \mathbb {P}^{1}$.
$\mathbb {P}^{n-1}\times \mathbb {P}^{1}$.
Lemma 3.8 For any ![]() $n$-dimensional toric Fano variety
$n$-dimensional toric Fano variety ![]() $X\!$ which is K-semistable,
$X\!$ which is K-semistable,
where ![]() $-K_{\mathbb {P}^{n}}$ is endowed with the volume-normalized Fubini–Study metric.
$-K_{\mathbb {P}^{n}}$ is endowed with the volume-normalized Fubini–Study metric.
Proof. Observe that the function of ![]() $\mathrm {vol}(X)$ appearing on the right-hand side of the inequality in the previous proposition is increasing when
$\mathrm {vol}(X)$ appearing on the right-hand side of the inequality in the previous proposition is increasing when ![]() $\mathrm {vol}(X)\leq (2\pi ^{2})^{n}/e$. This bound is, in fact, satisfied for any K-semistable
$\mathrm {vol}(X)\leq (2\pi ^{2})^{n}/e$. This bound is, in fact, satisfied for any K-semistable ![]() $X$. Indeed, by [Reference Berman and BerndtssonBB17],
$X$. Indeed, by [Reference Berman and BerndtssonBB17],
(using a simple induction argument in the last inequality). Thus, by the previous proposition, it will be enough to show that
for any ![]() $n\geq 2$. To this end, note that
$n\geq 2$. To this end, note that
We check that the inequality holds for ![]() $n=2$, and with induction in mind we simplify the right-hand side of (3.11) by
$n=2$, and with induction in mind we simplify the right-hand side of (3.11) by ![]() $n+1$ for
$n+1$ for ![]() $n$ and get
$n$ and get
 \begin{align*}
2\widehat{\mathrm{vol}}_{\chi}\bigl(-\overline{\mathcal{K}_{\mathbb{P}_{\mathbb{Z}}^{n+1}}}\bigr)
&=
-\frac{(n+2)^{n+1}}{(n+1)!}\biggl(n+1-(n+2)\sum_{k=1}^{n+1}\frac{1}{k}+\log((n+1)!)-(n+1)\log(\pi)\biggr)\\
&= -\biggl(\frac{n+2}{n+1}\biggr)^{n+1}\frac{(n+1)^{n}}{n!}
\Biggl(\biggl(n-(n+1)\sum_{k=1}^{n}\frac{1}{k}+\log(n!)-n\log(\pi)\biggr)\\
&\quad+
\biggl(1-(n+2)\sum_{k=1}^{n+1}\frac{1}{k}+(n+1)\sum_{k=1}^{n}\frac{1}{k}+\log(n+1)
-\log(\pi)\biggr)\Biggr)\\ &=
\biggl(\frac{n+2}{n+1}\biggr)^{n+1}2\widehat{\mathrm{vol}}_{\chi}
\bigl(-\overline{\mathcal{K}_{\mathbb{P}_{\mathbb{Z}}^{n}}}\bigr)
-\biggl(\frac{n+2}{n+1}\biggr)^{n+1}\biggl(1-\log(\pi)+\log(n+1)\\
&\quad-\frac{n+2}{n+1}
-\sum_{k=1}^{n}\frac{1}{k}\biggr).
\end{align*}
\begin{align*}
2\widehat{\mathrm{vol}}_{\chi}\bigl(-\overline{\mathcal{K}_{\mathbb{P}_{\mathbb{Z}}^{n+1}}}\bigr)
&=
-\frac{(n+2)^{n+1}}{(n+1)!}\biggl(n+1-(n+2)\sum_{k=1}^{n+1}\frac{1}{k}+\log((n+1)!)-(n+1)\log(\pi)\biggr)\\
&= -\biggl(\frac{n+2}{n+1}\biggr)^{n+1}\frac{(n+1)^{n}}{n!}
\Biggl(\biggl(n-(n+1)\sum_{k=1}^{n}\frac{1}{k}+\log(n!)-n\log(\pi)\biggr)\\
&\quad+
\biggl(1-(n+2)\sum_{k=1}^{n+1}\frac{1}{k}+(n+1)\sum_{k=1}^{n}\frac{1}{k}+\log(n+1)
-\log(\pi)\biggr)\Biggr)\\ &=
\biggl(\frac{n+2}{n+1}\biggr)^{n+1}2\widehat{\mathrm{vol}}_{\chi}
\bigl(-\overline{\mathcal{K}_{\mathbb{P}_{\mathbb{Z}}^{n}}}\bigr)
-\biggl(\frac{n+2}{n+1}\biggr)^{n+1}\biggl(1-\log(\pi)+\log(n+1)\\
&\quad-\frac{n+2}{n+1}
-\sum_{k=1}^{n}\frac{1}{k}\biggr).
\end{align*}
Here we observe for later use that ![]() $\widehat {\mathrm {vol}}_{\chi }(-\overline {\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n}}})>0$ for all
$\widehat {\mathrm {vol}}_{\chi }(-\overline {\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n}}})>0$ for all ![]() $n\geq 1$ by evaluating it at
$n\geq 1$ by evaluating it at ![]() $n=1$ and then using the above to perform induction and noting that
$n=1$ and then using the above to perform induction and noting that
 \[ -\biggl(1-\log(\pi)+\log(n+1)-\frac{n+2}{n+1}-\sum_{k=1}^{n}\frac{1}{k}\biggr)> -(-\log(\pi)+\log(2))=\log\biggl(\frac{\pi}{2}\biggr)>0 \]
\[ -\biggl(1-\log(\pi)+\log(n+1)-\frac{n+2}{n+1}-\sum_{k=1}^{n}\frac{1}{k}\biggr)> -(-\log(\pi)+\log(2))=\log\biggl(\frac{\pi}{2}\biggr)>0 \]
for ![]() $n\geq 1$. We have used that
$n\geq 1$. We have used that ![]() $-\log (n+1)+\sum _{k=1}^{n}({1}/{k})$ is increasing and can thus be estimated from below by putting
$-\log (n+1)+\sum _{k=1}^{n}({1}/{k})$ is increasing and can thus be estimated from below by putting ![]() $n=1$. We also simplify the left-hand side of (3.11),
$n=1$. We also simplify the left-hand side of (3.11),
 \begin{align*}
&-\mathrm{vol}(\mathbb{P}^{n}\times\mathbb{P}^{1})
\log(\mathrm{vol}(\mathbb{P}^{n}\times\mathbb{P}^{1})/(2\pi^{2})^{n+1})\\
&\quad= -\frac{2(n+1)^{n}}{n!}\biggl(\log\biggl(\frac{2(n+1)^{n}}{n!}\biggr) -(n+1)\log(2\pi^{2})\biggr)\\
&\quad = -\biggl(\frac{n+1}{n}\biggr)^{n}\frac{2n^{n}}{n!} \biggl(\log\biggl(\frac{2n^{n}}{n!}\biggr)-n\log(2\pi^{2})\biggr)\\
&\qquad+ \biggl(\log\biggl(\biggl(\frac{n+1}{n}\biggr)^{n}\biggr)-\log(2\pi^{2})\biggr)\\
&\quad = -\biggl(\frac{n+1}{n}\biggr)^{n}\mathrm{vol}(\mathbb{P}^{n-1}\times\mathbb{P}^{1})
\log(\mathrm{vol}(\mathbb{P}^{n-1}\times\mathbb{P}^{1})/(2\pi^{2})^{n})\\
&\qquad -2\frac{(n+1)^{n}}{n!}\biggl(-\log\biggl(\biggl(\frac{n+1}{n}\biggr)^{n}\biggr)-\log(2\pi^{2})\biggr).
\end{align*}
\begin{align*}
&-\mathrm{vol}(\mathbb{P}^{n}\times\mathbb{P}^{1})
\log(\mathrm{vol}(\mathbb{P}^{n}\times\mathbb{P}^{1})/(2\pi^{2})^{n+1})\\
&\quad= -\frac{2(n+1)^{n}}{n!}\biggl(\log\biggl(\frac{2(n+1)^{n}}{n!}\biggr) -(n+1)\log(2\pi^{2})\biggr)\\
&\quad = -\biggl(\frac{n+1}{n}\biggr)^{n}\frac{2n^{n}}{n!} \biggl(\log\biggl(\frac{2n^{n}}{n!}\biggr)-n\log(2\pi^{2})\biggr)\\
&\qquad+ \biggl(\log\biggl(\biggl(\frac{n+1}{n}\biggr)^{n}\biggr)-\log(2\pi^{2})\biggr)\\
&\quad = -\biggl(\frac{n+1}{n}\biggr)^{n}\mathrm{vol}(\mathbb{P}^{n-1}\times\mathbb{P}^{1})
\log(\mathrm{vol}(\mathbb{P}^{n-1}\times\mathbb{P}^{1})/(2\pi^{2})^{n})\\
&\qquad -2\frac{(n+1)^{n}}{n!}\biggl(-\log\biggl(\biggl(\frac{n+1}{n}\biggr)^{n}\biggr)-\log(2\pi^{2})\biggr).
\end{align*}
Fix ![]() $n\geq 2$ and assume
$n\geq 2$ and assume ![]() $-\mathrm {vol}(\mathbb {P}^{n-1}\times \mathbb {P}^{1})\log (\mathrm {vol}(\mathbb {P}^{n-1}\times \mathbb {P}^{1})/(2\pi ^{2})^{n})\leq 2\widehat {\mathrm {vol}}_{\chi } (-\overline {\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n}}})$. Define for brevity
$-\mathrm {vol}(\mathbb {P}^{n-1}\times \mathbb {P}^{1})\log (\mathrm {vol}(\mathbb {P}^{n-1}\times \mathbb {P}^{1})/(2\pi ^{2})^{n})\leq 2\widehat {\mathrm {vol}}_{\chi } (-\overline {\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n}}})$. Define for brevity ![]() $e_{n}=(1+{1}/{n})^{n}$ and estimate
$e_{n}=(1+{1}/{n})^{n}$ and estimate
 \begin{align*} & 2\widehat{\mathrm{vol}}_{\chi}\bigl(-\overline{\mathcal{K}_{\mathbb{P}_{\mathbb{Z}}^{n+1}}}\bigr)
-(-\mathrm{vol}(\mathbb{P}^{n}\times\mathbb{P}^{1})
\log(\mathrm{vol}(\mathbb{P}^{n}\times\mathbb{P}^{1})/(2\pi^{2})^{n+1}))\\ & \quad= e_{n+1}\widehat{\mathrm{vol}}_{\chi}
\bigl(-\overline{\mathcal{K}_{\mathbb{P}_{\mathbb{Z}}^{n}}}\bigr)
-(-e_{n}\mathrm{vol}(\mathbb{P}^{n}\times\mathbb{P}^{1})\log(\mathrm{vol}(\mathbb{P}^{n}\times\mathbb{P}^{1})/(2\pi^{2})^{n}))\\ & \qquad
+2\frac{(n+1)^{n}}{n!}\biggl(\log\biggl(\frac{(n+1)^{n}}{n}\biggr)-\log(2\pi^{2})\biggr)\\ & \qquad
-\frac{(n+2)^{n+1}}{(n+1)!}\biggl(1-\log(\pi)+\log(n+1)-\frac{n+2}{n+1}-\sum_{k=1}^{n}\frac{1}{k}\biggr)\\ & \quad >
2\frac{(n+1)^{n}}{n!}\biggl(\log\biggl(\frac{(n+1)^{n}}{n}\biggr)-\log(2\pi^{2})\biggr)\\ & \qquad -\frac{(n+2)^{n+1}}{(n+1)!}
\biggl(1-\log(\pi)+\log(n+1)-\frac{n+2}{n+1}-\sum_{k=1}^{n}\frac{1}{k}\biggr)\\ & \quad = \frac{(n+2)^{n+1}}{(n+1)!} \biggl(\frac{(n+1)^{n}}{n!}\biggl/\frac{(n+2)^{n+1}}{(n+1)!}
2\biggl(\log\biggl(\biggl(\frac{n+1}{n}\biggr)^{n}\biggr)-\log(2\pi^{2})\biggr)\\ & \qquad
-1+\log(\pi)-\log(n+1)+\frac{n+2}{n+1}+\sum_{k=1}^{n}\frac{1}{k}\biggr)\\ & \quad = \frac{(n+2)^{n+1}}{(n+1)!}
\biggl[\frac{2}{e_{n}}\bigl(\log(e_{n})-\log(2\pi^{2})\bigr)
+\log(\pi)+\sum_{k=1}^{n+1}\frac{1}{k}-\log(n+1)\biggr].
\end{align*}
\begin{align*} & 2\widehat{\mathrm{vol}}_{\chi}\bigl(-\overline{\mathcal{K}_{\mathbb{P}_{\mathbb{Z}}^{n+1}}}\bigr)
-(-\mathrm{vol}(\mathbb{P}^{n}\times\mathbb{P}^{1})
\log(\mathrm{vol}(\mathbb{P}^{n}\times\mathbb{P}^{1})/(2\pi^{2})^{n+1}))\\ & \quad= e_{n+1}\widehat{\mathrm{vol}}_{\chi}
\bigl(-\overline{\mathcal{K}_{\mathbb{P}_{\mathbb{Z}}^{n}}}\bigr)
-(-e_{n}\mathrm{vol}(\mathbb{P}^{n}\times\mathbb{P}^{1})\log(\mathrm{vol}(\mathbb{P}^{n}\times\mathbb{P}^{1})/(2\pi^{2})^{n}))\\ & \qquad
+2\frac{(n+1)^{n}}{n!}\biggl(\log\biggl(\frac{(n+1)^{n}}{n}\biggr)-\log(2\pi^{2})\biggr)\\ & \qquad
-\frac{(n+2)^{n+1}}{(n+1)!}\biggl(1-\log(\pi)+\log(n+1)-\frac{n+2}{n+1}-\sum_{k=1}^{n}\frac{1}{k}\biggr)\\ & \quad >
2\frac{(n+1)^{n}}{n!}\biggl(\log\biggl(\frac{(n+1)^{n}}{n}\biggr)-\log(2\pi^{2})\biggr)\\ & \qquad -\frac{(n+2)^{n+1}}{(n+1)!}
\biggl(1-\log(\pi)+\log(n+1)-\frac{n+2}{n+1}-\sum_{k=1}^{n}\frac{1}{k}\biggr)\\ & \quad = \frac{(n+2)^{n+1}}{(n+1)!} \biggl(\frac{(n+1)^{n}}{n!}\biggl/\frac{(n+2)^{n+1}}{(n+1)!}
2\biggl(\log\biggl(\biggl(\frac{n+1}{n}\biggr)^{n}\biggr)-\log(2\pi^{2})\biggr)\\ & \qquad
-1+\log(\pi)-\log(n+1)+\frac{n+2}{n+1}+\sum_{k=1}^{n}\frac{1}{k}\biggr)\\ & \quad = \frac{(n+2)^{n+1}}{(n+1)!}
\biggl[\frac{2}{e_{n}}\bigl(\log(e_{n})-\log(2\pi^{2})\bigr)
+\log(\pi)+\sum_{k=1}^{n+1}\frac{1}{k}-\log(n+1)\biggr].
\end{align*}
In the inequality above we have used ![]() $\widehat {\mathrm {vol}}_{\chi }(-\overline {\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n}}})>0$ for all
$\widehat {\mathrm {vol}}_{\chi }(-\overline {\mathcal {K}_{\mathbb {P}_{\mathbb {Z}}^{n}}})>0$ for all ![]() $n\geq 1$ and
$n\geq 1$ and ![]() $e_{n}< e_{n+1}$ and the induction hypothesis. Next check numerically that this last expression is positive for
$e_{n}< e_{n+1}$ and the induction hypothesis. Next check numerically that this last expression is positive for ![]() $n=2,3$. For
$n=2,3$. For ![]() $n\geq 4$ we have
$n\geq 4$ we have
 \begin{align*} &\frac{2}{e_{n}}\bigl(\log(e_{n})-\log(2\pi^{2})\bigr)+\log(\pi) +\sum_{k=1}^{n+1}\frac{1}{k}-\log(n+1)\\ &\quad > \frac{2}{e_{4}}(\log(e_{4})-\log(2\pi^{2}))+\log(\pi)+\gamma>0. \end{align*}
\begin{align*} &\frac{2}{e_{n}}\bigl(\log(e_{n})-\log(2\pi^{2})\bigr)+\log(\pi) +\sum_{k=1}^{n+1}\frac{1}{k}-\log(n+1)\\ &\quad > \frac{2}{e_{4}}(\log(e_{4})-\log(2\pi^{2}))+\log(\pi)+\gamma>0. \end{align*}
We used again that ![]() $e_{n}< e_{n+1}$ and the fact that
$e_{n}< e_{n+1}$ and the fact that ![]() ${\sum }_{k=1}^{n+1}({1}/{k})-\log (n+1)>\gamma$ [Reference Tims and TyrrellTT71], where
${\sum }_{k=1}^{n+1}({1}/{k})-\log (n+1)>\gamma$ [Reference Tims and TyrrellTT71], where ![]() $\gamma$ is the Euler–Mascheroni constant. The last inequality is checked numerically.
$\gamma$ is the Euler–Mascheroni constant. The last inequality is checked numerically.
We expect that any K-semistable toric Fano variety ![]() $X,$ not equal to
$X,$ not equal to ![]() $\mathbb {P}^{n},$ satisfies the volume bound in the previous lemma (see § 3.2.1). Here we will show that this is the case under the conditions of Theorem 1.2. First, the singular cases are handled using the following bound.
$\mathbb {P}^{n},$ satisfies the volume bound in the previous lemma (see § 3.2.1). Here we will show that this is the case under the conditions of Theorem 1.2. First, the singular cases are handled using the following bound.
Lemma 3.9 Let ![]() $X\!$ be a singular K-semistable toric Fano variety. Then
$X\!$ be a singular K-semistable toric Fano variety. Then
if any one of the following conditions holds.
•
 $X\!$ is
$X\!$ is  $\mathbb {Q}$-factorial (or equivalently,
$\mathbb {Q}$-factorial (or equivalently,  $X\!$ has abelian quotient singularities).
$X\!$ has abelian quotient singularities).•
 $X\!$ is not Gorenstein.
$X\!$ is not Gorenstein.
In particular, by the first point, when ![]() $n=2$ this inequality holds for any singular K-semistable toric Fano variety
$n=2$ this inequality holds for any singular K-semistable toric Fano variety ![]() $X$.
$X$.
Proof. The result concerning the first point is the toric case of [Reference LiuLiu18, Theorem 3] concerning quotient singularities, but in the toric case it also follows from the proof of [Reference Berman and BerndtssonBB17, Theorem 1.2]. For future reference we recall the argument in [Reference Berman and BerndtssonBB17]. Let ![]() $P$ be a given polytope with rational vertices and represent
$P$ be a given polytope with rational vertices and represent ![]() $P$ as the intersection of hyperplanes
$P$ as the intersection of hyperplanes ![]() $\{ p\in \mathbb {R}^{n}: \langle l_{F},p\rangle \geq -a_{F}\} ,$ where the index
$\{ p\in \mathbb {R}^{n}: \langle l_{F},p\rangle \geq -a_{F}\} ,$ where the index ![]() $F$ ranges over the facets of
$F$ ranges over the facets of ![]() $P,$
$P,$ ![]() $l_{F}$ is a primitive vector in
$l_{F}$ is a primitive vector in ![]() $\mathbb {Z}^{n}$ and
$\mathbb {Z}^{n}$ and ![]() $a_{F}$ is a positive number. In the present Fano case
$a_{F}$ is a positive number. In the present Fano case ![]() $a_{F}=1$. Moreover, since
$a_{F}=1$. Moreover, since ![]() $X\!$ is assumed to be
$X\!$ is assumed to be ![]() $\mathbb {Q}$-factorial for any vertex
$\mathbb {Q}$-factorial for any vertex ![]() $p_{0}$ of
$p_{0}$ of ![]() $P$ there are precisely
$P$ there are precisely ![]() $n$ facets
$n$ facets ![]() $F_{1},\ldots,F_{n}$ of
$F_{1},\ldots,F_{n}$ of ![]() $P$ intersecting
$P$ intersecting ![]() $p_{0},$ numbered so that the corresponding normals define a positively oriented basis in
$p_{0},$ numbered so that the corresponding normals define a positively oriented basis in ![]() $\mathbb {R}^{n}$ [Reference Cox, Little and SchenckCLS11]. Fixing a vertex
$\mathbb {R}^{n}$ [Reference Cox, Little and SchenckCLS11]. Fixing a vertex ![]() $p_{0}$ of
$p_{0}$ of ![]() $P$, we denote by
$P$, we denote by ![]() $P'$ the image of
$P'$ the image of ![]() $P$ under the map
$P$ under the map
which is a polytope in ![]() $[0,\infty [^{n}$. Moreover, assuming that
$[0,\infty [^{n}$. Moreover, assuming that ![]() $0$ is the barycenter of
$0$ is the barycenter of ![]() $P$, the barycenter of
$P$, the barycenter of ![]() $P'$ is
$P'$ is ![]() $(1,\ldots,1)$. By [Reference Berman and BerndtssonBB17, Theorem 1.5] the volume
$(1,\ldots,1)$. By [Reference Berman and BerndtssonBB17, Theorem 1.5] the volume ![]() $\mathrm {Vol}(P')$ of any such polytope is maximal when
$\mathrm {Vol}(P')$ of any such polytope is maximal when ![]() $P'$ is
$P'$ is ![]() $(n+1)$ times the unit simplex in
$(n+1)$ times the unit simplex in ![]() $[0,\infty [^{n}$ with vertex at
$[0,\infty [^{n}$ with vertex at ![]() $(0,\ldots,0)$. Hence,
$(0,\ldots,0)$. Hence,
where ![]() $\delta$ is the determinant of the map
$\delta$ is the determinant of the map ![]() $p\mapsto (\langle l_{F_{1}},p\rangle,\ldots,\langle l_{F_{n}},p\rangle )$. Thus
$p\mapsto (\langle l_{F_{1}},p\rangle,\ldots,\langle l_{F_{n}},p\rangle )$. Thus ![]() $\delta$ is a positive integer and
$\delta$ is a positive integer and ![]() $\delta =1$ if and only if the map is invertible, i.e. if and only if
$\delta =1$ if and only if the map is invertible, i.e. if and only if ![]() $l_{F_{1}},\ldots,l_{F_{n}}$ generate
$l_{F_{1}},\ldots,l_{F_{n}}$ generate ![]() $\mathbb {Z}^{n},$ which is equivalent to the
$\mathbb {Z}^{n},$ which is equivalent to the ![]() $T_{c}$-invariant neighborhood
$T_{c}$-invariant neighborhood ![]() $U_{0}$ corresponding to the vertex
$U_{0}$ corresponding to the vertex ![]() $p_{0}$ being biholomorphic to
$p_{0}$ being biholomorphic to ![]() $\mathbb {C}^{n}$ [Reference Cox, Little and SchenckCLS11]. Hence, if
$\mathbb {C}^{n}$ [Reference Cox, Little and SchenckCLS11]. Hence, if ![]() $X\!$ is singular (i.e.
$X\!$ is singular (i.e. ![]() $X\!$ is not non-singular), then there must be some vertex
$X\!$ is not non-singular), then there must be some vertex ![]() $p_{0}$ with
$p_{0}$ with ![]() $\delta \geq 2$. Since
$\delta \geq 2$. Since ![]() $a_{F_{i}}=1$, this concludes the proof.
$a_{F_{i}}=1$, this concludes the proof.
To prove the second point we employ a similar argument. This time, for ![]() $X\!$ possibly not
$X\!$ possibly not ![]() $\mathbb {Q}$-factorial, there might be more than
$\mathbb {Q}$-factorial, there might be more than ![]() $n$ facets intersecting a vertex
$n$ facets intersecting a vertex ![]() $p_{0}$. Still, there are at least
$p_{0}$. Still, there are at least ![]() $n$ facets intersecting at
$n$ facets intersecting at ![]() $p_{0}$, and we can construct the map (3.12) by choosing any
$p_{0}$, and we can construct the map (3.12) by choosing any ![]() $n$ of them. Next note that if
$n$ of them. Next note that if ![]() $\delta =1$, the map and its inverse have integer coefficients (since
$\delta =1$, the map and its inverse have integer coefficients (since ![]() $a_{F_{i}}=1$ when
$a_{F_{i}}=1$ when ![]() $X\!$ is Fano) and since
$X\!$ is Fano) and since ![]() $p_{0}$ is mapped to
$p_{0}$ is mapped to ![]() $0$,
$0$, ![]() $p_{0}\in \mathbb {Z}^{n}$. Since
$p_{0}\in \mathbb {Z}^{n}$. Since ![]() $p_{0}$ was arbitrary, it follows that
$p_{0}$ was arbitrary, it follows that ![]() $P$ is a lattice polytope and hence
$P$ is a lattice polytope and hence ![]() $X\!$ is Gorenstein. Thus
$X\!$ is Gorenstein. Thus ![]() $\delta \geq 2$ and we are done.
$\delta \geq 2$ and we are done.
The volume bound in the previous lemma implies the volume bound in Lemma 3.8 is satisfied:
The left-hand side in the latter inequality increases to ![]() $e,$ which is, indeed, smaller than
$e,$ which is, indeed, smaller than ![]() $4$. This proves Theorem 1.2 in the singular cases. Finally, in the case that
$4$. This proves Theorem 1.2 in the singular cases. Finally, in the case that ![]() $X\!$ is non-singular there are, for any given dimension
$X\!$ is non-singular there are, for any given dimension ![]() $n$, only a finite number of cases to check in order to verify the volume bound in Lemma 3.8. When
$n$, only a finite number of cases to check in order to verify the volume bound in Lemma 3.8. When ![]() $n\leq 6$ we may apply the database [Reference ØbroØbr07] of all non-singular Fano varieties of dimension
$n\leq 6$ we may apply the database [Reference ØbroØbr07] of all non-singular Fano varieties of dimension ![]() $n$. The condition that the barycenter of
$n$. The condition that the barycenter of ![]() $P$ vanishes corresponds in the database to the condition ‘zero dual barycenter’. Adding the condition
$P$ vanishes corresponds in the database to the condition ‘zero dual barycenter’. Adding the condition ![]() $(-K_{X}\!)^{n}\geq n!\mathrm {vol}(\mathbb {P}^{n-1}\times \mathbb {P}^{1})$, the database only furnishes
$(-K_{X}\!)^{n}\geq n!\mathrm {vol}(\mathbb {P}^{n-1}\times \mathbb {P}^{1})$, the database only furnishes ![]() $\mathbb {P}^{n}$ and
$\mathbb {P}^{n}$ and ![]() $\mathbb {P}^{n-1}\times \mathbb {P}^{1}$, as desired.
$\mathbb {P}^{n-1}\times \mathbb {P}^{1}$, as desired.
3.2.1 Remarks on the ‘gap hypothesis’
In order to extend the proof of Theorem 1.2 to any dimension ![]() $n$ one would need to establish the following conjecture (established above under the conditions in Theorem 1.2).
$n$ one would need to establish the following conjecture (established above under the conditions in Theorem 1.2).
Conjecture 3.10 (The ‘gap hypothesis’)
For any ![]() $n$-dimensional toric K-semistable Fano manifold
$n$-dimensional toric K-semistable Fano manifold ![]() $X\!$ different from
$X\!$ different from ![]() $\mathbb {P}^{n},$
$\mathbb {P}^{n},$ ![]() $\mathrm {vol}(X)\leq \mathrm {vol}(\mathbb {P}^{n-1}\times \mathbb {P}^{1})$.
$\mathrm {vol}(X)\leq \mathrm {vol}(\mathbb {P}^{n-1}\times \mathbb {P}^{1})$.
This conjecture might even hold without the toric assumptions in any dimension (as pointed out to us by Ziquan Zhuang, this appears to be a folklore conjecture). For example, when ![]() $n=3$ and
$n=3$ and ![]() $X\!$ is non-singular it follows from the well-known classification of three-dimensional Fano manifolds (see the ‘big table’ in [Reference AraujoAra+, § 6]) that the only Fano manifolds
$X\!$ is non-singular it follows from the well-known classification of three-dimensional Fano manifolds (see the ‘big table’ in [Reference AraujoAra+, § 6]) that the only Fano manifolds ![]() $X\!$, different from
$X\!$, different from ![]() $\mathbb {P}^{3},$ which do not satisfy the inequality in question are
$\mathbb {P}^{3},$ which do not satisfy the inequality in question are ![]() $\mathbb {P}^{3}$ blown up at one point and
$\mathbb {P}^{3}$ blown up at one point and ![]() $\mathbb {P}(\mathcal {O}\oplus \mathcal {O}(2))$. But both of these are K-unstable, i.e. they are not K-semistable. Indeed, these two Fano manifolds are toric and if they were K-semistable they would satisfy the gap hypothesis, by the toric case
$\mathbb {P}(\mathcal {O}\oplus \mathcal {O}(2))$. But both of these are K-unstable, i.e. they are not K-semistable. Indeed, these two Fano manifolds are toric and if they were K-semistable they would satisfy the gap hypothesis, by the toric case ![]() $(n\leq 6)$ applied to
$(n\leq 6)$ applied to ![]() $n=3$. Let us also point out that in the toric case it is only
$n=3$. Let us also point out that in the toric case it is only ![]() $\mathbb {P}^{n-1}\times \mathbb {P}^{1}$ that saturates the inequality in the ‘gap hypothesis’ when
$\mathbb {P}^{n-1}\times \mathbb {P}^{1}$ that saturates the inequality in the ‘gap hypothesis’ when ![]() $n\leq 6$ and it thus seems natural to ask if this is also the case when
$n\leq 6$ and it thus seems natural to ask if this is also the case when ![]() $n>6$. However, in the general non-toric case the inequality is also saturated by the non-singular quadratic hypersurface
$n>6$. However, in the general non-toric case the inequality is also saturated by the non-singular quadratic hypersurface ![]() $X_{2}$ in
$X_{2}$ in ![]() $\mathbb {P}^{n+1},$ i.e. the base of the ordinary double point (ODP). Moreover, as pointed out to us by Yuji Odaka, in the general case our ‘gap hypothesis’ is reminiscent of the ODP conjecture in [Reference Spotti and SunSS17], very recently settled in the toric case [Reference Moraga and SüßMS24]. More precisely, in our setup, the ODP conjecture implies that
$\mathbb {P}^{n+1},$ i.e. the base of the ordinary double point (ODP). Moreover, as pointed out to us by Yuji Odaka, in the general case our ‘gap hypothesis’ is reminiscent of the ODP conjecture in [Reference Spotti and SunSS17], very recently settled in the toric case [Reference Moraga and SüßMS24]. More precisely, in our setup, the ODP conjecture implies that
where ![]() $I(X)$ denotes the Fano index of
$I(X)$ denotes the Fano index of ![]() $X\!$ (i.e. the largest positive integer such that
$X\!$ (i.e. the largest positive integer such that ![]() $K_{X}/I(X)$ is a line bundle). However,
$K_{X}/I(X)$ is a line bundle). However, ![]() $I(X)\leq n$ when
$I(X)\leq n$ when ![]() $X\neq \mathbb {P}^{n}$ (with equality if and only if
$X\neq \mathbb {P}^{n}$ (with equality if and only if ![]() $X=X_{2})$ and hence inequality (3.15) is weaker than our ‘gap hypothesis’.
$X=X_{2})$ and hence inequality (3.15) is weaker than our ‘gap hypothesis’.
3.2.2 The case of products in any dimension
Lemma 3.11 The ‘gap hypothesis’ holds when ![]() $X\!$ is the product of K-semistable Fano varieties
$X\!$ is the product of K-semistable Fano varieties ![]() $X_{1},\ldots.,X_{M}$ (not necessarily assumed toric), for
$X_{1},\ldots.,X_{M}$ (not necessarily assumed toric), for ![]() $M\geq 2$.
$M\geq 2$.
Proof. By a simple induction argument we may as well assume that ![]() $M=2$. Without loss of generality, let
$M=2$. Without loss of generality, let ![]() $n:=\mathrm {dim}(X_{1})\geq \dim (X_{2})=:m>1$. Note that if
$n:=\mathrm {dim}(X_{1})\geq \dim (X_{2})=:m>1$. Note that if ![]() $m=1$ we are done, since then
$m=1$ we are done, since then ![]() $\mathrm {vol}(X)=\mathrm {vol}(X_{1})\mathrm {vol}(X_{2})\leq \mathrm {vol}(\mathbb {\mathbb {P}}^{N-1})\mathrm {vol}(\mathbb {P}^{1})=\mathrm {vol}(\mathbb {P}^{N-1}\times \mathbb {P}^{1})$ using that, by Fujita's inequality (1.1), the complex projective space maximizes the volume among K-semistable Fano varieties in each dimension. Using again that the complex projective space maximizes the volume in each given dimension and defining for brevity
$\mathrm {vol}(X)=\mathrm {vol}(X_{1})\mathrm {vol}(X_{2})\leq \mathrm {vol}(\mathbb {\mathbb {P}}^{N-1})\mathrm {vol}(\mathbb {P}^{1})=\mathrm {vol}(\mathbb {P}^{N-1}\times \mathbb {P}^{1})$ using that, by Fujita's inequality (1.1), the complex projective space maximizes the volume among K-semistable Fano varieties in each dimension. Using again that the complex projective space maximizes the volume in each given dimension and defining for brevity ![]() $e_{k}:=(1+{1}/{k})^{k}$, we get
$e_{k}:=(1+{1}/{k})^{k}$, we get
 \begin{align*} \mathrm{vol}(X)&=\mathrm{vol}(X_{1})\mathrm{vol}(X_{2})\leq\mathrm{vol}(\mathbb{\mathbb{P}}^{n})\mathrm{vol}(\mathbb{P}^{m})\\ &=\frac{(n+1)^{n}}{n!}\frac{(m+1)^{m}}{m!} =\frac{(n+2)^{n+1}}{(n+1)!}\frac{m^{m-1}}{(m-1)!}\biggl(\frac{n+1}{n+2}\biggr)^{n+1}\biggl(\frac{m+1}{m}\biggr)^{m}\\ &=\frac{(n+2)^{n+1}}{(n+1)!}\frac{m^{m-1}}{(m-1)!}\frac{e_{m}}{e_{n+1}} <\frac{(n+2)^{n+1}}{(n+1)!}\frac{m^{m-1}}{(m-1)!} =\mathrm{vol}(\mathbb{\mathbb{P}}^{n+1})\mathrm{vol}(\mathbb{P}^{m-1}), \end{align*}
\begin{align*} \mathrm{vol}(X)&=\mathrm{vol}(X_{1})\mathrm{vol}(X_{2})\leq\mathrm{vol}(\mathbb{\mathbb{P}}^{n})\mathrm{vol}(\mathbb{P}^{m})\\ &=\frac{(n+1)^{n}}{n!}\frac{(m+1)^{m}}{m!} =\frac{(n+2)^{n+1}}{(n+1)!}\frac{m^{m-1}}{(m-1)!}\biggl(\frac{n+1}{n+2}\biggr)^{n+1}\biggl(\frac{m+1}{m}\biggr)^{m}\\ &=\frac{(n+2)^{n+1}}{(n+1)!}\frac{m^{m-1}}{(m-1)!}\frac{e_{m}}{e_{n+1}} <\frac{(n+2)^{n+1}}{(n+1)!}\frac{m^{m-1}}{(m-1)!} =\mathrm{vol}(\mathbb{\mathbb{P}}^{n+1})\mathrm{vol}(\mathbb{P}^{m-1}), \end{align*}
where in the last inequality we have used that ![]() $e_{k}$ is increasing in
$e_{k}$ is increasing in ![]() $k$. We may continue in similar manner until we have
$k$. We may continue in similar manner until we have ![]() $\mathrm {vol}(\mathbb {P}^{N-1}\times \mathbb {P}^{1})$ in the right-hand side and we are done.
$\mathrm {vol}(\mathbb {P}^{N-1}\times \mathbb {P}^{1})$ in the right-hand side and we are done.
As explained in the previous section, it follows from the previous lemma that Conjecture 1.1 holds when ![]() $\mathcal {X}$ is a product of toric arithmetic Fano varieties, i.e.
$\mathcal {X}$ is a product of toric arithmetic Fano varieties, i.e. ![]() $\mathcal {X}=\mathcal {X}_{1}\times \cdots \times \mathcal {X}_{M},$ where
$\mathcal {X}=\mathcal {X}_{1}\times \cdots \times \mathcal {X}_{M},$ where ![]() $\mathcal {X}_{i}$ is endowed with its canonical integral structure.
$\mathcal {X}_{i}$ is endowed with its canonical integral structure.
3.3 The height of toric Kähler–Einstein metrics; proof of Theorem 1.3
By Proposition 3.7 it only remains to prove the lower bound. Using the notation in the proof of Proposition 3.7 we have that, for any continuous convex function ![]() $\psi$ on
$\psi$ on ![]() $\mathbb {R}^{n}$ such that
$\mathbb {R}^{n}$ such that ![]() $\psi -\psi _{P}$ is bounded,
$\psi -\psi _{P}$ is bounded,
In particular, taking ![]() $\psi =\psi _{P}$, the first term on the right-hand side vanishes. Moreover,
$\psi =\psi _{P}$, the first term on the right-hand side vanishes. Moreover,
where ![]() $P^{*}$ denotes the polar dual of
$P^{*}$ denotes the polar dual of ![]() $P$, i.e.
$P$, i.e. ![]() $P^{*}$ consists of all
$P^{*}$ consists of all ![]() $x\in \mathbb {R}^{n}$ such that
$x\in \mathbb {R}^{n}$ such that ![]() $x\cdot p\leq 1$ for all
$x\cdot p\leq 1$ for all ![]() $p\in P$. Indeed,
$p\in P$. Indeed,
where ![]() $V(t)$ is the Lebesgue volume of
$V(t)$ is the Lebesgue volume of ![]() $\{\psi _{P}< t\}$, i.e. of
$\{\psi _{P}< t\}$, i.e. of ![]() $tP^{*}$. Hence,
$tP^{*}$. Hence,
Since, by definition, ![]() $\mathrm {Vol}(P^{*})\mathrm {Vol}(P)\geq m_{n}$ this concludes the proof of the lower bound in the theorem. Next, by [Reference KuperbergKup08, Corollary 1.8] (see also [Reference BerndtssonBer21]),
$\mathrm {Vol}(P^{*})\mathrm {Vol}(P)\geq m_{n}$ this concludes the proof of the lower bound in the theorem. Next, by [Reference KuperbergKup08, Corollary 1.8] (see also [Reference BerndtssonBer21]),
where ![]() $\sigma _{n}={{\mathrm {vol}}{(\mathbb {P}^{n}).}}$ Since
$\sigma _{n}={{\mathrm {vol}}{(\mathbb {P}^{n}).}}$ Since ![]() $\mathrm {Vol}(P)\leq \sigma _{n}$ (by (3.10)) this means that
$\mathrm {Vol}(P)\leq \sigma _{n}$ (by (3.10)) this means that
proving the positivity in the theorem.
3.4 Examples
We next provide examples of families of toric varieties ![]() $X\!$ for which the height of the corresponding Kähler–Einstein can be explicitly computed as a function of
$X\!$ for which the height of the corresponding Kähler–Einstein can be explicitly computed as a function of ![]() $\mathrm {vol}(X)$ of the same form as in Theorem 1.3. The examples are based on the following proposition.
$\mathrm {vol}(X)$ of the same form as in Theorem 1.3. The examples are based on the following proposition.
Proposition 3.12 Let ![]() $X_{1}$ and
$X_{1}$ and ![]() $X_{2}$ be two K-semistable toric Fano varieties of dimension
$X_{2}$ be two K-semistable toric Fano varieties of dimension ![]() $n$ with moment polytopes
$n$ with moment polytopes ![]() $P_{1}$ and
$P_{1}$ and ![]() $P_{2}$ such that
$P_{2}$ such that ![]() $P_{2}=AP_{1}$ for an invertible linear transformation
$P_{2}=AP_{1}$ for an invertible linear transformation ![]() $A$ (the polytopes are linearly equivalent). Denote the canonical integral models of
$A$ (the polytopes are linearly equivalent). Denote the canonical integral models of ![]() $X_{1}$ and
$X_{1}$ and ![]() $X_{2}$ by
$X_{2}$ by ![]() $\mathcal {X}_{1}$ and
$\mathcal {X}_{1}$ and ![]() $\mathcal {X}_{2}$, respectively. Then, with heights taken with respect to the volume-normalized Kähler–Einstein metrics,
$\mathcal {X}_{2}$, respectively. Then, with heights taken with respect to the volume-normalized Kähler–Einstein metrics,
 \[ \frac{\bigl(\overline{-\mathcal{K}_{\mathcal{X}_{2}}}\bigr)^{n+1}/(n+1)!} {(-K_{X_{2}})^{n}/n!}=\frac{\bigl(\overline{-\mathcal{K}_{\mathcal{X}_{1}}}\bigr)^{n+1}/(n+1)!} {(-K_{X_{1}})^{n}/n!}-\frac{1}{2}\log\mathrm{det}A. \]
\[ \frac{\bigl(\overline{-\mathcal{K}_{\mathcal{X}_{2}}}\bigr)^{n+1}/(n+1)!} {(-K_{X_{2}})^{n}/n!}=\frac{\bigl(\overline{-\mathcal{K}_{\mathcal{X}_{1}}}\bigr)^{n+1}/(n+1)!} {(-K_{X_{1}})^{n}/n!}-\frac{1}{2}\log\mathrm{det}A. \]
As a consequence, for ![]() $X\!$ a K-semistable toric Fano variety of dimension
$X\!$ a K-semistable toric Fano variety of dimension ![]() $n$,
$n$,
where ![]() $a$ is a constant independent of the choice of
$a$ is a constant independent of the choice of ![]() $X\!$ within a class of toric varieties with linearly equivalent moment polytopes. More precisely,
$X\!$ within a class of toric varieties with linearly equivalent moment polytopes. More precisely,
 \begin{equation} a=\mathrm{vol}(X)\exp\biggl(\frac{2\bigl(\overline{-\mathcal{K}_{\mathcal{X}}}\bigr)^{n+1}/(n+1)!} {\mathrm{vol}(X)}\biggr) \end{equation}
\begin{equation} a=\mathrm{vol}(X)\exp\biggl(\frac{2\bigl(\overline{-\mathcal{K}_{\mathcal{X}}}\bigr)^{n+1}/(n+1)!} {\mathrm{vol}(X)}\biggr) \end{equation}and Proposition 3.12 ensures the claimed independence.
Proof of Proposition 3.12 Recall that, with heights taken with respect to Kähler–Einstein metrics,
 \[ \frac{\bigl(\overline{-\mathcal{K}_{\mathcal{X}_{2}}}\bigr)^{n+1}/(n+1)!} {(-K_{X_{2}})^{n}/n!}=-\frac{1}{2}\sup_{\phi}-\frac{1}{\mathrm{vol}(P_{2})} \int_{P_{2}}\phi^{*}(p)\,{d}p+\log\int_{\mathbb{R}^{n}}\exp(-\phi(x))\,{d} x. \]
\[ \frac{\bigl(\overline{-\mathcal{K}_{\mathcal{X}_{2}}}\bigr)^{n+1}/(n+1)!} {(-K_{X_{2}})^{n}/n!}=-\frac{1}{2}\sup_{\phi}-\frac{1}{\mathrm{vol}(P_{2})} \int_{P_{2}}\phi^{*}(p)\,{d}p+\log\int_{\mathbb{R}^{n}}\exp(-\phi(x))\,{d} x. \]
Changing variables in the integrals, ![]() $p\mapsto A^{t}p'$ and
$p\mapsto A^{t}p'$ and ![]() $x\mapsto Ax'$, we get
$x\mapsto Ax'$, we get
 \begin{align*}
&\frac{(\overline{-\mathcal{K}_{\mathcal{X}_{2}}})^{n+1}/(n+1)!}{(-K_{X_{2}})^{n}/n!} \\
&\quad =-\frac{1}{2}\biggl(\sup_{\phi(A\cdot)}-\frac{1}{\mathrm{vol}(P_{1})}
\int_{P_{1}}\phi^{*}(A^{t}p')\,{d}p'+\log\int_{\mathbb{R}^{n}}\exp(-\phi(Ax'))\,{d}
x'+\log \mathrm{detA}\biggr). \end{align*}
\begin{align*}
&\frac{(\overline{-\mathcal{K}_{\mathcal{X}_{2}}})^{n+1}/(n+1)!}{(-K_{X_{2}})^{n}/n!} \\
&\quad =-\frac{1}{2}\biggl(\sup_{\phi(A\cdot)}-\frac{1}{\mathrm{vol}(P_{1})}
\int_{P_{1}}\phi^{*}(A^{t}p')\,{d}p'+\log\int_{\mathbb{R}^{n}}\exp(-\phi(Ax'))\,{d}
x'+\log \mathrm{detA}\biggr). \end{align*}
Now we rename ![]() $\phi '=\phi (A\cdot )$ and use that then
$\phi '=\phi (A\cdot )$ and use that then ![]() $\phi '^{*}=\phi ^{*}(A^{t}\cdot )$ to get the result.
$\phi '^{*}=\phi ^{*}(A^{t}\cdot )$ to get the result.
Example 3.13 Recall the K-semistable toric Fano varieties ![]() $X_{q,p}$ parametrized with two prime numbers from Example 3.1. The corresponding polytope
$X_{q,p}$ parametrized with two prime numbers from Example 3.1. The corresponding polytope ![]() $P(-K_{X_{p,q}})$ is the image of the polytope
$P(-K_{X_{p,q}})$ is the image of the polytope ![]() $P(-K_{\mathbb {P}^{1}\times \mathbb {P}^{1}})=\mathrm {conv}\{(1,1),(1,-1),(-1,1),(-1,-1)\}$ under the linear map
$P(-K_{\mathbb {P}^{1}\times \mathbb {P}^{1}})=\mathrm {conv}\{(1,1),(1,-1),(-1,1),(-1,-1)\}$ under the linear map ![]() $A$ given in matrix form by
$A$ given in matrix form by ![]() $\left [\begin{smallmatrix} {1}/{2p} & {1}/{2p}\\ {-1}/{2q} & {1}/{2q}\end{smallmatrix}\right ]$. Thus the family
$\left [\begin{smallmatrix} {1}/{2p} & {1}/{2p}\\ {-1}/{2q} & {1}/{2q}\end{smallmatrix}\right ]$. Thus the family ![]() $\mathcal {F}=\{\mathbb {P}^{1}\times \mathbb {P}^{1},X_{p,q}:p,q\ \mathrm {prime\}}$ comprises an example of a family of K-semistable toric Fano varieties with linearly equivalent moment polytopes. Thus by (3.16), for
$\mathcal {F}=\{\mathbb {P}^{1}\times \mathbb {P}^{1},X_{p,q}:p,q\ \mathrm {prime\}}$ comprises an example of a family of K-semistable toric Fano varieties with linearly equivalent moment polytopes. Thus by (3.16), for ![]() $X\in \mathcal {F}$,
$X\in \mathcal {F}$,
with, by (3.17), Lemma 3.6 and a simple computation,
 \[ a=\mathrm{vol}(\mathbb{P}^{1}\times\mathbb{P}^{1}) \exp\biggl(\frac{2\bigl(\overline{-\mathcal{K}_{\mathbb{P}^{1}\times\mathbb{P}^{1}}}\bigr)^{n+1}/(n+1)!} {\mathrm{vol}(\mathbb{P}^{1}\times\mathbb{P}^{1})}\biggr) =4\exp(2-\log\pi^{2}). \]
\[ a=\mathrm{vol}(\mathbb{P}^{1}\times\mathbb{P}^{1}) \exp\biggl(\frac{2\bigl(\overline{-\mathcal{K}_{\mathbb{P}^{1}\times\mathbb{P}^{1}}}\bigr)^{n+1}/(n+1)!} {\mathrm{vol}(\mathbb{P}^{1}\times\mathbb{P}^{1})}\biggr) =4\exp(2-\log\pi^{2}). \]
Recall also that ![]() $\mathrm {vol }{(-K_{X_{p,q}})}=2/(pq)$, so that in this family the heights with respect to the Kähler–Einstein metrics are explicitly computed by the previous formula.
$\mathrm {vol }{(-K_{X_{p,q}})}=2/(pq)$, so that in this family the heights with respect to the Kähler–Einstein metrics are explicitly computed by the previous formula.
4. Sharp bounds on Donaldson's toric Mabuchi functional
Let ![]() $(X,L)$ be a polarized complex manifold and denote by
$(X,L)$ be a polarized complex manifold and denote by ![]() $\mathcal {H}(X,L)$ the space of all smooth metrics
$\mathcal {H}(X,L)$ the space of all smooth metrics ![]() $\psi$ on
$\psi$ on ![]() $L$ whose curvature form
$L$ whose curvature form ![]() $dd^{c}\psi$ is positive,
$dd^{c}\psi$ is positive, ![]() $dd^{c}\psi >0$.
$dd^{c}\psi >0$.
4.1 The Mabuchi functional (recap)
The Mabuchi functional ![]() $\mathcal {M}$ on
$\mathcal {M}$ on ![]() $\mathcal {H}(X,L)$ is defined, up to addition by a constant, by declaring that its differential on
$\mathcal {H}(X,L)$ is defined, up to addition by a constant, by declaring that its differential on ![]() $\mathcal {H}(X,L)$ at a given point
$\mathcal {H}(X,L)$ at a given point ![]() $\psi$ is represented by the following measure on
$\psi$ is represented by the following measure on ![]() $X\!$:
$X\!$:
where ![]() $S(\psi )$ denotes the scalar curvature of the Kähler form
$S(\psi )$ denotes the scalar curvature of the Kähler form ![]() $(dd^{c}\psi ),$ i.e. the trace of the Ricci curvature,
$(dd^{c}\psi ),$ i.e. the trace of the Ricci curvature,
Recall that the Ricci curvature ![]() $\mathrm {Ric}(dd^{c}\psi )$ of the Kähler form
$\mathrm {Ric}(dd^{c}\psi )$ of the Kähler form ![]() $dd^{c}\psi$ is the
$dd^{c}\psi$ is the ![]() $(1,1)$-form defined as the curvature of the metric on
$(1,1)$-form defined as the curvature of the metric on ![]() $-K_{X\!}$ induced by the volume form of
$-K_{X\!}$ induced by the volume form of ![]() $dd^{c}\psi$. We have followed Donaldson's multiplicative normalizations in [Reference DonaldsonDon02, formula (3.2.1)], which differ from the original definition in [Reference MabuchiMab86], where the measure
$dd^{c}\psi$. We have followed Donaldson's multiplicative normalizations in [Reference DonaldsonDon02, formula (3.2.1)], which differ from the original definition in [Reference MabuchiMab86], where the measure ![]() ${(dd^{c}\psi )^{n}}/{n!}$ on
${(dd^{c}\psi )^{n}}/{n!}$ on ![]() $X\!$ is volume-normalized. At any rate, formula (4.1) only determines the Mabuchi functional
$X\!$ is volume-normalized. At any rate, formula (4.1) only determines the Mabuchi functional ![]() $\mathcal {M}$ up to an additive constant.
$\mathcal {M}$ up to an additive constant.
4.1.1 The case when  $X\!$ is a Fano manifold and
$X\!$ is a Fano manifold and  $L=-K_{X\!}$
$L=-K_{X\!}$
We now specialize to the case when ![]() $L=-K_{X\!}$ and note that a choice of reference metric
$L=-K_{X\!}$ and note that a choice of reference metric ![]() $\psi _{0}$ in
$\psi _{0}$ in ![]() $\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$ induces a particular choice of Mabuchi functional, i.e. a functional whose differential satisfies formula (4.1), which we shall denote by
$\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$ induces a particular choice of Mabuchi functional, i.e. a functional whose differential satisfies formula (4.1), which we shall denote by ![]() $\mathcal {M}_{\psi _{0}}$. This is a consequence of the thermodynamical formalism introduced in [Reference BermanBer13], which expresses
$\mathcal {M}_{\psi _{0}}$. This is a consequence of the thermodynamical formalism introduced in [Reference BermanBer13], which expresses
where ![]() $MA(\psi )$ is the probability measure on
$MA(\psi )$ is the probability measure on ![]() $X\!$ defined by the normalized volume form of the Kähler metric
$X\!$ defined by the normalized volume form of the Kähler metric ![]() $dd^{c}\psi$,
$dd^{c}\psi$,
and ![]() $F_{\psi _{0}}\big (\mu \big )$ denotes the free energy functional on the space
$F_{\psi _{0}}\big (\mu \big )$ denotes the free energy functional on the space ![]() $\mathcal {P}(X)$ of all probability measures on
$\mathcal {P}(X)$ of all probability measures on ![]() $X\!$, defined as
$X\!$, defined as
Here ![]() $\mathrm {Ent}_{dV_{0}}(\mu )$ denotes the entropy of
$\mathrm {Ent}_{dV_{0}}(\mu )$ denotes the entropy of ![]() $\mu$ relative to the volume form
$\mu$ relative to the volume form ![]() $dV_{0}$ on
$dV_{0}$ on ![]() $X\!$ induced by
$X\!$ induced by ![]() $\psi _{0}$ (i.e.
$\psi _{0}$ (i.e. ![]() $dV_{0}=e^{-\psi _{0}}$ in the notation of § 2.1.2) defined by
$dV_{0}=e^{-\psi _{0}}$ in the notation of § 2.1.2) defined by
when ![]() $\mu \in L^{1}(X,dV_{0})$ and otherwise
$\mu \in L^{1}(X,dV_{0})$ and otherwise ![]() $\mathrm {Ent}_{dV_{0}}(\mu ):=\infty$. Furthermore,
$\mathrm {Ent}_{dV_{0}}(\mu ):=\infty$. Furthermore, ![]() $E_{\psi _{0}}(\mu )$ is the pluricomplex energy of
$E_{\psi _{0}}(\mu )$ is the pluricomplex energy of ![]() $\mu,$ relative to
$\mu,$ relative to ![]() $\psi _{0},$ introduced in [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13], which may be defined as a Legendre–Fenchel transform of the functional
$\psi _{0},$ introduced in [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13], which may be defined as a Legendre–Fenchel transform of the functional ![]() $\mathcal {E}_{\psi _{0}}/\mathrm {vol}(L)$ (defined by formula (2.11)). For our purposes it will be enough to define
$\mathcal {E}_{\psi _{0}}/\mathrm {vol}(L)$ (defined by formula (2.11)). For our purposes it will be enough to define ![]() $E_{\psi _{0}}(\mu )$ when
$E_{\psi _{0}}(\mu )$ when ![]() $\mu$ is of the form
$\mu$ is of the form ![]() $\mu =MA(\psi )$ for
$\mu =MA(\psi )$ for ![]() $\psi$ in
$\psi$ in ![]() $\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$:
$\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$:
We recall that formula (4.2) follows readily from the fact that on the subspace of all volume forms ![]() $\mu$ in
$\mu$ in ![]() $\mathcal {P}(X)$ the differential of
$\mathcal {P}(X)$ the differential of ![]() $E_{\psi _{0}}$ at
$E_{\psi _{0}}$ at ![]() $\mu \in \mathcal {P}(X)$ is represented by the function
$\mu \in \mathcal {P}(X)$ is represented by the function ![]() $\psi _{0}-\psi _{\mu }$:
$\psi _{0}-\psi _{\mu }$:
(this formula is dual to formula (2.12) in the sense of Legendre transforms; see [Reference BermanBer13]).
Remark 4.1 Formula (4.2) defines ![]() $\mathcal {M}_{\psi _{0}}(\psi )$ on the space
$\mathcal {M}_{\psi _{0}}(\psi )$ on the space ![]() $\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$ as a function taking values in
$\mathcal {C}^{0}(L)\cap \mathrm {PSH}{(L)}$ as a function taking values in ![]() $]{-}\infty,\infty ]$. More generally, the functional
$]{-}\infty,\infty ]$. More generally, the functional ![]() $\mathcal {M}_{\psi _{0}}(\psi )$ is well defined as soon as
$\mathcal {M}_{\psi _{0}}(\psi )$ is well defined as soon as ![]() $E(MA(\psi ))<\infty$ (see [Reference BermanBer13, Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19]). For
$E(MA(\psi ))<\infty$ (see [Reference BermanBer13, Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19]). For ![]() $\psi$ smooth, formula (4.2) is essentially equivalent to a formula for the Mabuchi functional appearing in [Reference TianTia96] and [Reference ChenChe00].
$\psi$ smooth, formula (4.2) is essentially equivalent to a formula for the Mabuchi functional appearing in [Reference TianTia96] and [Reference ChenChe00].
4.1.2 The case when  $X\!$ is a singular Fano variety
$X\!$ is a singular Fano variety
In the case when ![]() $X\!$ is a singular Fano variety we will denote by
$X\!$ is a singular Fano variety we will denote by ![]() $\mathcal {H}(X,-K_{X}\!)$ the space of all continuous metrics
$\mathcal {H}(X,-K_{X}\!)$ the space of all continuous metrics ![]() $\psi$ on
$\psi$ on ![]() $L$ such that
$L$ such that ![]() $\psi$ is smooth on the regular locus
$\psi$ is smooth on the regular locus ![]() $X_{\mathrm {reg}}$ of
$X_{\mathrm {reg}}$ of ![]() $X\!$ and
$X\!$ and ![]() $dd^{c}\psi >0$ on
$dd^{c}\psi >0$ on ![]() $X_{\mathrm {reg}}$.
$X_{\mathrm {reg}}$.
4.2 Proof of Theorem 1.5
Recall the basic inequality that holds on any Fano variety [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19, Lemma 4.4],
as follows from the non-negativity of the relative entropy between two probability measures (or Jensen's inequality). In fact, the following identity holds [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19, Lemma 4.4]:
(the two infima above may, equivalently, be restricted to ![]() $\mathcal {H}(X,L)$; see the regularization result in [Reference Berman, Darvas and LuBDL17]).
$\mathcal {H}(X,L)$; see the regularization result in [Reference Berman, Darvas and LuBDL17]).
Combining Theorem 1.2 with inequality (4.6), the proof is concluded by invoking the following formula relating ![]() $\mathcal {M}_{\psi _{P}}$(where
$\mathcal {M}_{\psi _{P}}$(where ![]() $\psi _{P}$ is the canonical toric reference defined by formula (3.3)) to Donaldson's toric Mabuchi functional
$\psi _{P}$ is the canonical toric reference defined by formula (3.3)) to Donaldson's toric Mabuchi functional
where ![]() $\psi ^{*}$ denotes the Legendre transform of the
$\psi ^{*}$ denotes the Legendre transform of the ![]() $T$-invariant metric
$T$-invariant metric ![]() $\psi \in \mathcal {H}(X,-K_{X}\!)$ and
$\psi \in \mathcal {H}(X,-K_{X}\!)$ and ![]() $d\sigma$ is the measure on
$d\sigma$ is the measure on ![]() $\partial P,$ absolutely continuous with respect to the
$\partial P,$ absolutely continuous with respect to the ![]() $(n-1)$-dimensional Lebesgue measure
$(n-1)$-dimensional Lebesgue measure ![]() $d\lambda _{\partial P},$ defined by
$d\lambda _{\partial P},$ defined by ![]() $d\sigma =d\lambda _{\partial P}/\Vert l_{F}\Vert$ on a facet
$d\sigma =d\lambda _{\partial P}/\Vert l_{F}\Vert$ on a facet ![]() $F$ of
$F$ of ![]() $\partial P,$ where
$\partial P,$ where ![]() $\Vert l_{F}\Vert$ denotes the Euclidean norm of a primitive normal vector to
$\Vert l_{F}\Vert$ denotes the Euclidean norm of a primitive normal vector to ![]() $F$.
$F$.
Lemma 4.2 Let ![]() $X\!$ be an
$X\!$ be an ![]() $n$-dimensional toric Fano variety. The following identity holds on the space of all
$n$-dimensional toric Fano variety. The following identity holds on the space of all ![]() $T$-invariant metrics in
$T$-invariant metrics in ![]() $\mathcal {H}(X,-K_{X}\!)$:
$\mathcal {H}(X,-K_{X}\!)$:
Proof. This formula is essentially the content of [Reference Berman and BerndtssonBB13, Proposition 4.6], but since the normalizations are a bit different we recall the proof. Identifying a toric metric ![]() $\psi$ with a convex function on
$\psi$ with a convex function on ![]() $\mathbb {R}^{n}$ (as in § 3.1.2), formula (4.2), combined with formula (4.5), yields
$\mathbb {R}^{n}$ (as in § 3.1.2), formula (4.2), combined with formula (4.5), yields
 \begin{align*}
\mathcal{M}_{\psi_{P}}(\psi)
&=-\mathcal{E}_{\psi_{P}}(\psi)+\int_{\mathbb{R}^{n}}
(\psi-\psi_{P})(dd^{c}\psi)^{n}/n!+\int_{\mathbb{R}^{n}}\log
\biggl(\frac{MA(\psi)}{e^{-\psi_{P}}\,dx}\biggr)\mathrm{vol}(-K_{X})MA(\psi)\\
&=\int_{P}\psi^{*}\,d\lambda+\int_{\mathbb{R}^{n}}\psi(dd^{c}\psi)^{n}/n!
+\int_{\mathbb{R}^{n}}\log\det(\nabla^{2}\psi)\det(\nabla^{2}\psi) \\
&\quad -\mathrm{vol}(-K_{X})\log\mathrm{vol}(-K_{X}\!).
\end{align*}
\begin{align*}
\mathcal{M}_{\psi_{P}}(\psi)
&=-\mathcal{E}_{\psi_{P}}(\psi)+\int_{\mathbb{R}^{n}}
(\psi-\psi_{P})(dd^{c}\psi)^{n}/n!+\int_{\mathbb{R}^{n}}\log
\biggl(\frac{MA(\psi)}{e^{-\psi_{P}}\,dx}\biggr)\mathrm{vol}(-K_{X})MA(\psi)\\
&=\int_{P}\psi^{*}\,d\lambda+\int_{\mathbb{R}^{n}}\psi(dd^{c}\psi)^{n}/n!
+\int_{\mathbb{R}^{n}}\log\det(\nabla^{2}\psi)\det(\nabla^{2}\psi) \\
&\quad -\mathrm{vol}(-K_{X})\log\mathrm{vol}(-K_{X}\!).
\end{align*}
By [Reference Berman and BerndtssonBB13, Lemma 4.7], making the change of variables ![]() $y=\nabla \psi$, the second term above may be expressed as
$y=\nabla \psi$, the second term above may be expressed as
giving
Again making the change of variables ![]() $y=\nabla \psi$ in the remaining integral over
$y=\nabla \psi$ in the remaining integral over ![]() $\mathbb {R}^{n}$ concludes the proof, using the standard relation
$\mathbb {R}^{n}$ concludes the proof, using the standard relation ![]() $\det (\nabla ^{2}\psi )(x)\det (\nabla ^{2}\psi ^{*})(\nabla \psi (x))=1$ (which follows from the fact that the map
$\det (\nabla ^{2}\psi )(x)\det (\nabla ^{2}\psi ^{*})(\nabla \psi (x))=1$ (which follows from the fact that the map ![]() $y\mapsto \nabla \psi ^{*}(y)$ is the inverse of
$y\mapsto \nabla \psi ^{*}(y)$ is the inverse of ![]() $x\mapsto \nabla \psi (x)$).
$x\mapsto \nabla \psi (x)$).
5. Relations to the arithmetic Mabuchi functional
Given an integral model ![]() $(\mathcal {X},\mathcal {L})$ of a polarized variety
$(\mathcal {X},\mathcal {L})$ of a polarized variety ![]() $(X,L)$, consider the arithmetic Mabuchi functional
$(X,L)$, consider the arithmetic Mabuchi functional ![]() $\mathcal {M}_{(\mathcal {X},\mathcal {L})}$ on
$\mathcal {M}_{(\mathcal {X},\mathcal {L})}$ on ![]() $\mathcal {H}(X,L)$ defined by
$\mathcal {H}(X,L)$ defined by
where ![]() $\overline {\mathcal {L}}=(\mathcal {L},\psi )$ and
$\overline {\mathcal {L}}=(\mathcal {L},\psi )$ and ![]() $\overline {\mathcal {K}}_{\mathcal {X}}$ is endowed with the metric induced by the measure
$\overline {\mathcal {K}}_{\mathcal {X}}$ is endowed with the metric induced by the measure ![]() $MA(\psi )$ on
$MA(\psi )$ on ![]() $X,$ i.e. the normalized volume form of the Kähler form
$X,$ i.e. the normalized volume form of the Kähler form ![]() $dd^{c}\psi$. As discussed in § 1.4, this functional coincides, up to additive and multiplicative normalizations, with the arithmetic Mabuchi functional introduced in [Reference OdakaOda18].
$dd^{c}\psi$. As discussed in § 1.4, this functional coincides, up to additive and multiplicative normalizations, with the arithmetic Mabuchi functional introduced in [Reference OdakaOda18].
Lemma 5.1 The differential of the functional ![]() $\psi \mapsto 2\mathcal {M}_{(\mathcal {X},\mathcal {L})}(\mathcal {L},\psi )$ on
$\psi \mapsto 2\mathcal {M}_{(\mathcal {X},\mathcal {L})}(\mathcal {L},\psi )$ on ![]() $\mathcal {H}(X,L)$ satisfies the defining formula (4.1) of the Mabuchi functional.
$\mathcal {H}(X,L)$ satisfies the defining formula (4.1) of the Mabuchi functional.
Proof. As pointed out in [Reference OdakaOda18], this formula can be deduced from the formula for the Mabuchi functional in [Reference TianTia96, Reference ChenChe00]. But for completeness and to check the normalizations we provide a simple direct proof. Recall the following property of arithmetic intersection numbers which holds if ![]() $\mathcal {L}_{0}\rightarrow \mathcal {X}$ is the trivial line bundle (which is a consequence of the restriction formula [Reference Bost, Gillet and SouléBGS94, Proposition 2.3.1] and Lemma 2.3):
$\mathcal {L}_{0}\rightarrow \mathcal {X}$ is the trivial line bundle (which is a consequence of the restriction formula [Reference Bost, Gillet and SouléBGS94, Proposition 2.3.1] and Lemma 2.3):
where ![]() $\phi _{0}$ is the globally well-defined function on
$\phi _{0}$ is the globally well-defined function on ![]() $X\!$ defined by formula (2.1) when
$X\!$ defined by formula (2.1) when ![]() $e_{U}$ is the standard global trivialization
$e_{U}$ is the standard global trivialization ![]() $1$ of the trivial line bundle over
$1$ of the trivial line bundle over ![]() $X\!$, i.e.
$X\!$, i.e. ![]() $\phi _{0}/2=-\log \Vert s \Vert _{\phi _{0}},$ in which
$\phi _{0}/2=-\log \Vert s \Vert _{\phi _{0}},$ in which ![]() $s$ is a global trivialization of
$s$ is a global trivialization of ![]() $\mathcal {L}$. In particular, differentiating along a curve
$\mathcal {L}$. In particular, differentiating along a curve ![]() $t\mapsto \psi _{t}$ in
$t\mapsto \psi _{t}$ in ![]() $\mathcal {H}(X,L)$ and using the symmetry of arithmetic intersection numbers gives
$\mathcal {H}(X,L)$ and using the symmetry of arithmetic intersection numbers gives
where ![]() ${d\psi _{t}}/{dt}$ is a globally well-defined function on
${d\psi _{t}}/{dt}$ is a globally well-defined function on ![]() $X\!$ and can thus be identified with a metric on the trivial line bundle that we denote by
$X\!$ and can thus be identified with a metric on the trivial line bundle that we denote by ![]() $\mathcal {L}_{0}$. Likewise, denoting by
$\mathcal {L}_{0}$. Likewise, denoting by ![]() $\rho _{t}$ a local density for
$\rho _{t}$ a local density for ![]() $MA(\psi _{t})$ with respect to the Euclidean measure defined by local holomorphic coordinates,
$MA(\psi _{t})$ with respect to the Euclidean measure defined by local holomorphic coordinates,
where we have used Leibniz's rule. Applying formula (5.2), the second term above may, after multiplication by ![]() $2,$ be expressed as
$2,$ be expressed as
using in the last equality that ![]() $\int _{X}\rho _{t}=\mathrm {vol}(L)$ for any
$\int _{X}\rho _{t}=\mathrm {vol}(L)$ for any ![]() $t$. Likewise, applying formula (5.2) to the first term in formula (5.3) yields
$t$. Likewise, applying formula (5.2) to the first term in formula (5.3) yields
This concludes the proof.
The following proposition relates the arithmetic Mabuchi functional ![]() $\mathcal {M}_{(\mathcal {X},\mathcal {-K_{\mathcal {X}}})}$ to Donaldson's toric Mabuchi functional
$\mathcal {M}_{(\mathcal {X},\mathcal {-K_{\mathcal {X}}})}$ to Donaldson's toric Mabuchi functional ![]() $\mathcal {M}_{-K_{X}}$ (formula (4.8)).
$\mathcal {M}_{-K_{X}}$ (formula (4.8)).
Proposition 5.2 Given a toric Fano variety ![]() $X\!$, denote by
$X\!$, denote by ![]() $\mathcal {X}$ its canonical integral model. Then the following formula holds for any
$\mathcal {X}$ its canonical integral model. Then the following formula holds for any ![]() $T$-invariant metric in
$T$-invariant metric in ![]() $\mathcal {H}(X,-K_{X}\!)$:
$\mathcal {H}(X,-K_{X}\!)$:
Proof. In this case ![]() $a=n$ and we can thus decompose
$a=n$ and we can thus decompose ![]() $\mathcal {M}_{(\mathcal {X},\mathcal {L})}(\psi )$ as
$\mathcal {M}_{(\mathcal {X},\mathcal {L})}(\psi )$ as
where, in the last equality, we have exploited that ![]() $\mathcal {L}+\mathcal {K}_{\mathcal {X}}$ is trivial so that formula (5.2) applies. Applying formula (3.7) to the first term on the right-hand side above thus gives
$\mathcal {L}+\mathcal {K}_{\mathcal {X}}$ is trivial so that formula (5.2) applies. Applying formula (3.7) to the first term on the right-hand side above thus gives
 \begin{align*} 2\mathcal{M}_{(\mathcal{X},\mathcal{L})}(\psi)&:=-\mathcal{E}_{\psi_{P}}(\psi)+\int\log\biggl(\frac{MA(\psi)}{e^{-\psi}}\biggr)(dd^{c}\psi)^{n}/n!\\ &=\mathrm{vol}(-K_{X})\biggl(-\frac{1}{V(X)}\mathcal{E}_{\psi_{P}}(\psi)+\langle \psi-\psi_{P},MA(\psi)\rangle +\int\log\biggl(\frac{MA(\psi)}{e^{-\psi_{P}}}\biggr)MA(\psi)\biggr). \end{align*}
\begin{align*} 2\mathcal{M}_{(\mathcal{X},\mathcal{L})}(\psi)&:=-\mathcal{E}_{\psi_{P}}(\psi)+\int\log\biggl(\frac{MA(\psi)}{e^{-\psi}}\biggr)(dd^{c}\psi)^{n}/n!\\ &=\mathrm{vol}(-K_{X})\biggl(-\frac{1}{V(X)}\mathcal{E}_{\psi_{P}}(\psi)+\langle \psi-\psi_{P},MA(\psi)\rangle +\int\log\biggl(\frac{MA(\psi)}{e^{-\psi_{P}}}\biggr)MA(\psi)\biggr). \end{align*}
The right-hand side in the last equation above equals ![]() $\mathcal {M}_{\psi _{P}}(\psi )$ (by definition (4.2)). Invoking Lemma 4.2 thus concludes the proof.
$\mathcal {M}_{\psi _{P}}(\psi )$ (by definition (4.2)). Invoking Lemma 4.2 thus concludes the proof.
Next, consider an arithmetic Fano variety ![]() $\mathcal {X}$ (defined in § 2.2.1). Denote by
$\mathcal {X}$ (defined in § 2.2.1). Denote by ![]() $\mathcal {\hat {D}}_{\mathbb {Z}}(\psi )$ the functional defined by formula (2.15), corresponding to the integral model
$\mathcal {\hat {D}}_{\mathbb {Z}}(\psi )$ the functional defined by formula (2.15), corresponding to the integral model ![]() $\mathcal {L}=-\mathcal {K}_{\mathcal {X}}$. In this arithmetic setup the following variants of inequality (4.6) and identity (4.7) hold.
$\mathcal {L}=-\mathcal {K}_{\mathcal {X}}$. In this arithmetic setup the following variants of inequality (4.6) and identity (4.7) hold.
Proposition 5.3 When ![]() $\mathcal {L}=-\mathcal {K}_{\mathcal {X}}$ the following relations hold:
$\mathcal {L}=-\mathcal {K}_{\mathcal {X}}$ the following relations hold:
and
Proof. First, note that the second term in the decomposition (5.4) of ![]() $\mathcal {M}_{(\mathcal {X},-\mathcal {K}_{\mathcal {X}})}(\psi )$ is precisely the entropy of
$\mathcal {M}_{(\mathcal {X},-\mathcal {K}_{\mathcal {X}})}(\psi )$ is precisely the entropy of ![]() $(dd^{c}\psi )^{n}/n!$ relative to
$(dd^{c}\psi )^{n}/n!$ relative to ![]() $e^{-\psi }$:
$e^{-\psi }$:
Since the entropy between two probability measure is non-negative (by Jensen's inequality) this proves the inequality in the proposition when the measure ![]() $e^{-\psi }$ has unit total volume. The general case then follows from a simple scaling argument.
$e^{-\psi }$ has unit total volume. The general case then follows from a simple scaling argument.
Next, to prove the identity in the proposition fix a reference metric ![]() $\psi _{0}$ in
$\psi _{0}$ in ![]() $\mathcal {H}(X,-K_{X}\!)$ and rewrite the previous formula as
$\mathcal {H}(X,-K_{X}\!)$ and rewrite the previous formula as
Accordingly, expressing ![]() $(\mathcal {L},\psi )^{n+1}=(\mathcal {L},\psi _{0})^{n+1}+(n+1)!\mathcal {E}_{\psi _{0}}(\psi )/2,$ using Lemma 2.9, gives
$(\mathcal {L},\psi )^{n+1}=(\mathcal {L},\psi _{0})^{n+1}+(n+1)!\mathcal {E}_{\psi _{0}}(\psi )/2,$ using Lemma 2.9, gives
where ![]() $F_{\psi _{0}}(\mu )$ is the free energy functional (4.4). The proof is thus concluded by invoking the identity (4.7) and using Lemma 2.9 again.
$F_{\psi _{0}}(\mu )$ is the free energy functional (4.4). The proof is thus concluded by invoking the identity (4.7) and using Lemma 2.9 again.
Remark 5.4 When ![]() $-K_{X\!}$ admits a Kähler–Einstein metric
$-K_{X\!}$ admits a Kähler–Einstein metric ![]() $\phi _{\mathrm {KE}}$ both infima in the previous proposition are attained at
$\phi _{\mathrm {KE}}$ both infima in the previous proposition are attained at ![]() $\phi _{\mathrm {KE}}$ [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19]. The identity then follows directly from the Kähler–Einstein equation, giving
$\phi _{\mathrm {KE}}$ [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ19]. The identity then follows directly from the Kähler–Einstein equation, giving ![]() $MA(\phi _{\mathrm {KE}})=e^{-\phi _{\mathrm {KE}}},$ when
$MA(\phi _{\mathrm {KE}})=e^{-\phi _{\mathrm {KE}}},$ when ![]() $\phi _{\mathrm {KE}}$ is volume-normalized.
$\phi _{\mathrm {KE}}$ is volume-normalized.
In § 6.2 the inequality in the previous proposition will be generalized to any model ![]() $(\mathcal {X},\mathcal {L})$ of
$(\mathcal {X},\mathcal {L})$ of ![]() $(X,-K_{X}),$ by introducing an arithmetic Ding functional
$(X,-K_{X}),$ by introducing an arithmetic Ding functional ![]() $\mathcal {D}_{(\mathcal {X},\mathcal {L})}$, coinciding (up to normalization) with the functional
$\mathcal {D}_{(\mathcal {X},\mathcal {L})}$, coinciding (up to normalization) with the functional ![]() $\mathcal {\hat {D}}_{\mathbb {Z}}$ under the conditions in the previous proposition.
$\mathcal {\hat {D}}_{\mathbb {Z}}$ under the conditions in the previous proposition.
6. Discussion and outlook
6.1 The function field analog
Recall that, according to the philosophy of Arakelov geometry, the function field analog of a metrized arithmetic variety ![]() $\mathcal {X}\rightarrow \mathrm {Spec }{\mathbb {Z}}$ is a flat projective morphism
$\mathcal {X}\rightarrow \mathrm {Spec }{\mathbb {Z}}$ is a flat projective morphism
from a normal complex projective variety ![]() $\mathcal {\mathscr {X}}$ to a fixed regular complex projective curve
$\mathcal {\mathscr {X}}$ to a fixed regular complex projective curve ![]() $\mathcal {\mathscr {B}}$. In particular, the analog of the setup of arithmetic Fano varieties in Conjecture 1.1 appears when
$\mathcal {\mathscr {B}}$. In particular, the analog of the setup of arithmetic Fano varieties in Conjecture 1.1 appears when ![]() $\mathcal {\mathscr {X}}$ is normal, the relative anti-canonical divisor
$\mathcal {\mathscr {X}}$ is normal, the relative anti-canonical divisor ![]() $-\mathcal {\mathscr {K}}_{\mathscr {X}/\mathscr {B}}$ defines a relatively ample
$-\mathcal {\mathscr {K}}_{\mathscr {X}/\mathscr {B}}$ defines a relatively ample ![]() $\mathbb {Q}$-line bundle and the generic fiber is K-semistable. The analog of the inequality in Conjecture 1.1 does hold in this situation, but not the uniqueness statement. More precisely, if
$\mathbb {Q}$-line bundle and the generic fiber is K-semistable. The analog of the inequality in Conjecture 1.1 does hold in this situation, but not the uniqueness statement. More precisely, if ![]() $(X,-K_{X}\!)$ is assumed K-semistable then it follows from [Reference Codogni and PatakfalviCP21] (see the beginning of [Reference Codogni and PatakfalviCP21, § 1.7.1]) that
$(X,-K_{X}\!)$ is assumed K-semistable then it follows from [Reference Codogni and PatakfalviCP21] (see the beginning of [Reference Codogni and PatakfalviCP21, § 1.7.1]) that
Equality holds for the trivial fibrations ![]() $\mathcal {\mathscr {X}}=X\times \mathcal {\mathscr {B}}$ for any K-semistable
$\mathcal {\mathscr {X}}=X\times \mathcal {\mathscr {B}}$ for any K-semistable ![]() $X$. In particular,
$X$. In particular,
which is the function field analog of the inequality in Conjecture 1.1. Note that when ![]() $\mathcal {\mathscr {B}}=\mathbb {P}^{1}$ and the standard
$\mathcal {\mathscr {B}}=\mathbb {P}^{1}$ and the standard ![]() $\mathbb {C}^{*}$-action on
$\mathbb {C}^{*}$-action on ![]() $\mathbb {P}^{1}$ lifts to
$\mathbb {P}^{1}$ lifts to ![]() $\mathcal {\mathscr {X}}$, inequality (6.1) follows directly from the definition of K-semistability.
$\mathcal {\mathscr {X}}$, inequality (6.1) follows directly from the definition of K-semistability.
Remark 6.1 The analog of the volume normalization (appearing in Conjecture 1.1) is automatically satisfied in the function field case. Indeed, the second term in the corresponding Ding functional ![]() $\mathcal {D}_{(\mathcal {X}_{\mathscr {X}/\mathscr {B}},-\mathcal {\mathscr {K}}_{\mathscr {X}/\mathscr {B}})},$ discussed in the following section, then vanishes.
$\mathcal {D}_{(\mathcal {X}_{\mathscr {X}/\mathscr {B}},-\mathcal {\mathscr {K}}_{\mathscr {X}/\mathscr {B}})},$ discussed in the following section, then vanishes.
In contrast to Conjecture 1.1, projective space thus plays no special role in the function field case (since equality holds in the inequality (6.2) for any product ![]() $\mathcal {\mathscr {X}}=X\times \mathcal {\mathscr {B}})$. Conversely, it should be stressed that the analog of inequality (6.1) fails in the arithmetic situation (by the strict positivity in Lemma 3.6). Hence, the function field analogy is somewhat deceptive. Our general motivation for Conjecture 1.1 is rather the analogy with the corresponding result over
$\mathcal {\mathscr {X}}=X\times \mathcal {\mathscr {B}})$. Conversely, it should be stressed that the analog of inequality (6.1) fails in the arithmetic situation (by the strict positivity in Lemma 3.6). Hence, the function field analogy is somewhat deceptive. Our general motivation for Conjecture 1.1 is rather the analogy with the corresponding result over ![]() $\mathbb {C}$ (corresponding to the trivial morphism
$\mathbb {C}$ (corresponding to the trivial morphism ![]() $X\rightarrow \mathrm {Spec}{\mathbb {C}})$ and the fact that projective space maximizes the degree of
$X\rightarrow \mathrm {Spec}{\mathbb {C}})$ and the fact that projective space maximizes the degree of ![]() $-K_{X\!}$ [Reference FujitaFuj18], among K-semistable
$-K_{X\!}$ [Reference FujitaFuj18], among K-semistable ![]() $X\!$ of a given dimension (as well as a range of other positivity properties of
$X\!$ of a given dimension (as well as a range of other positivity properties of ![]() $-K_{X\!}$; see, for example, the discussion and references in the introduction to [Reference Liu and ZhuangLZ18]).
$-K_{X\!}$; see, for example, the discussion and references in the introduction to [Reference Liu and ZhuangLZ18]).
6.2 A generalization of Conjecture 1.1
Consider a Fano variety ![]() $X_{F}$ defined over a number field
$X_{F}$ defined over a number field ![]() $F,$ i.e. a field extension
$F,$ i.e. a field extension ![]() $F$ of
$F$ of ![]() $\mathbb {Q}$ of finite degree
$\mathbb {Q}$ of finite degree ![]() $[F:\mathbb {Q}]$. Let
$[F:\mathbb {Q}]$. Let ![]() $(\mathcal {X},\mathcal {L})$ be a normal polarized model of
$(\mathcal {X},\mathcal {L})$ be a normal polarized model of ![]() $(X_{F},-K_{X_{F}}\!)$ over the ring of integers
$(X_{F},-K_{X_{F}}\!)$ over the ring of integers ![]() $\mathcal {O}_{F}$ of
$\mathcal {O}_{F}$ of ![]() $F$ such that
$F$ such that ![]() $\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}$ is defined as a
$\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}$ is defined as a ![]() $\mathbb {Q}$-line bundle. We will denote by
$\mathbb {Q}$-line bundle. We will denote by ![]() $\psi$ a collection of continuous psh
$\psi$ a collection of continuous psh ![]() $\psi _{\sigma }$ metrics on
$\psi _{\sigma }$ metrics on ![]() $-K_{X_{\sigma }},$ where
$-K_{X_{\sigma }},$ where ![]() $\sigma$ ranges over all embeddings of the field
$\sigma$ ranges over all embeddings of the field ![]() $F$ into
$F$ into ![]() $\mathbb {C}$ and
$\mathbb {C}$ and ![]() $X_{\sigma }$ denotes the corresponding complex projective varieties. To the model
$X_{\sigma }$ denotes the corresponding complex projective varieties. To the model ![]() $(\mathcal {X},\mathcal {L})$ we attach an arithmetic Ding functional, defined as follows. First consider a model
$(\mathcal {X},\mathcal {L})$ we attach an arithmetic Ding functional, defined as follows. First consider a model ![]() $(\mathcal {X},\mathcal {L})$ of
$(\mathcal {X},\mathcal {L})$ of ![]() $(X_{F},-K_{X_{F}}\!)$ such that
$(X_{F},-K_{X_{F}}\!)$ such that ![]() $\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}$ defines a bona fide line bundle. Then
$\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}$ defines a bona fide line bundle. Then
in which ![]() $\mathcal {\hat {D}}_{(\mathcal {X},\mathcal {L})}(\psi )$ is the normalized arithmetic Ding functional defined by
$\mathcal {\hat {D}}_{(\mathcal {X},\mathcal {L})}(\psi )$ is the normalized arithmetic Ding functional defined by
where the second term denotes the arithmetic (Arakelov) degree of the line bundle ![]() $\pi _{*}(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)\rightarrow \mathrm {Spec}\mathcal {O}_{F},$ endowed with the
$\pi _{*}(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)\rightarrow \mathrm {Spec}\mathcal {O}_{F},$ endowed with the ![]() $L^{2}$-metric induced by the metric
$L^{2}$-metric induced by the metric ![]() $\psi$ on
$\psi$ on ![]() $\mathcal {L}$ (i.e. on
$\mathcal {L}$ (i.e. on ![]() $-K_{X}\!)$. More generally, when
$-K_{X}\!)$. More generally, when ![]() $\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}$ is merely defined as a
$\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}$ is merely defined as a ![]() $\mathbb {Q}$-line bundle we fix a positive integer
$\mathbb {Q}$-line bundle we fix a positive integer ![]() $r$ such that
$r$ such that ![]() $r(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)$ is defined as a line bundle and replace
$r(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)$ is defined as a line bundle and replace ![]() $\widehat {\deg }\pi _{*}(\mathcal {X},(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)$ with
$\widehat {\deg }\pi _{*}(\mathcal {X},(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)$ with ![]() $r^{-1}\widehat {\deg }\pi _{*}(\mathcal {X},(r(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)),$ where now
$r^{-1}\widehat {\deg }\pi _{*}(\mathcal {X},(r(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)),$ where now ![]() $\pi _{*}(r(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!))$ is endowed with the
$\pi _{*}(r(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!))$ is endowed with the ![]() $L^{2/r}$-metric induced by
$L^{2/r}$-metric induced by ![]() $\psi$. Concretely, given a rational global section
$\psi$. Concretely, given a rational global section ![]() $s_{r}$ of
$s_{r}$ of ![]() $\pi _{*}(r(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)),$ one may express
$\pi _{*}(r(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)),$ one may express
 \begin{equation} \widehat{\deg}\pi_{*}(r(\mathcal{L}+\mathcal{K}_{\mathcal{X}/\mathrm{Spec}{\mathcal{O}_{F}}}))=-\frac{1}{2}\sum_{\sigma}\log\int_{X_{\sigma}}|s_{r}|^{2/r}e^{-\psi_{\sigma}}+\sum_{\mathfrak{p}}\mathrm{ord}_{\mathfrak{p}}(s_{r})\log\!|\mathfrak{p}|, \end{equation}
\begin{equation} \widehat{\deg}\pi_{*}(r(\mathcal{L}+\mathcal{K}_{\mathcal{X}/\mathrm{Spec}{\mathcal{O}_{F}}}))=-\frac{1}{2}\sum_{\sigma}\log\int_{X_{\sigma}}|s_{r}|^{2/r}e^{-\psi_{\sigma}}+\sum_{\mathfrak{p}}\mathrm{ord}_{\mathfrak{p}}(s_{r})\log\!|\mathfrak{p}|, \end{equation}
where ![]() $|s_{r}|^{2/r}e^{-\psi _{\sigma }}$ denotes corresponding measure on
$|s_{r}|^{2/r}e^{-\psi _{\sigma }}$ denotes corresponding measure on ![]() $X_{\sigma },$
$X_{\sigma },$ ![]() $\mathrm {ord}_{\mathfrak {p}}(s)$ denotes the order of vanishing of
$\mathrm {ord}_{\mathfrak {p}}(s)$ denotes the order of vanishing of ![]() $s_{r}$ at the closed point
$s_{r}$ at the closed point ![]() $\mathfrak {p}$ in
$\mathfrak {p}$ in ![]() $\mathrm {Spec}\mathcal {O}_{F}$ and
$\mathrm {Spec}\mathcal {O}_{F}$ and ![]() $|\mathfrak {p}|$ denotes the norm of the prime ideal in
$|\mathfrak {p}|$ denotes the norm of the prime ideal in ![]() $\mathcal {O}_{F}$ defined by
$\mathcal {O}_{F}$ defined by ![]() $\mathfrak {p}$ (i.e. the cardinality of the corresponding residue field
$\mathfrak {p}$ (i.e. the cardinality of the corresponding residue field ![]() $\mathcal {O}_{F}/\mathfrak {p}$). The functional
$\mathcal {O}_{F}/\mathfrak {p}$). The functional ![]() $\mathcal {\hat {D}}_{(\mathcal {X},\mathcal {L})}$ thus coincides with the functional
$\mathcal {\hat {D}}_{(\mathcal {X},\mathcal {L})}$ thus coincides with the functional ![]() $\mathcal {\hat {D}}_{\mathbb {Z}},$ defined in formula (2.15), up to an additive constant and a factor of
$\mathcal {\hat {D}}_{\mathbb {Z}},$ defined in formula (2.15), up to an additive constant and a factor of ![]() $2$. Note that when
$2$. Note that when ![]() $F=\mathbb {Q}$ and
$F=\mathbb {Q}$ and ![]() $\mathcal {L}=-\mathcal {K}_{\mathcal {X}}$ we have
$\mathcal {L}=-\mathcal {K}_{\mathcal {X}}$ we have ![]() $2\widehat {\deg }\pi _{*}(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)=-\log \int _{X}e^{-\phi }$. Indeed, in this we can take
$2\widehat {\deg }\pi _{*}(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)=-\log \int _{X}e^{-\phi }$. Indeed, in this we can take ![]() $s_{r}=1\in H^{0}(\mathcal {X},\mathcal {O}_{\mathcal {X}}),$ which is globally non-vanishing, by Lemma 2.3.
$s_{r}=1\in H^{0}(\mathcal {X},\mathcal {O}_{\mathcal {X}}),$ which is globally non-vanishing, by Lemma 2.3.
Remark 6.2 The functional ![]() $\mathcal {D}_{(\mathcal {X},\mathcal {L})}(\psi )$ is the arithmetic analog of the degree of the Ding line bundle of a test configuration
$\mathcal {D}_{(\mathcal {X},\mathcal {L})}(\psi )$ is the arithmetic analog of the degree of the Ding line bundle of a test configuration ![]() $(\mathscr {X},\mathscr {L})$ for
$(\mathscr {X},\mathscr {L})$ for ![]() $(X,-K_{X}\!)$ introduced in [Reference BermanBer16]. As shown in [Reference FujitaFuj19], a Fano variety
$(X,-K_{X}\!)$ introduced in [Reference BermanBer16]. As shown in [Reference FujitaFuj19], a Fano variety ![]() $X\!$ is K-semistable if and only if the degree of the Ding line bundle is non-negative for any test configuration
$X\!$ is K-semistable if and only if the degree of the Ding line bundle is non-negative for any test configuration ![]() $(\mathscr {X},\mathscr {L})$.
$(\mathscr {X},\mathscr {L})$.
Now consider the following invariant of the Fano variety ![]() $X_{F}$:
$X_{F}$:
where the infimum runs over all integral models ![]() $(\mathcal {X},\mathcal {L})$ of
$(\mathcal {X},\mathcal {L})$ of ![]() $(X,-K_{X}\!)$ and metrics
$(X,-K_{X}\!)$ and metrics ![]() $\psi$ as above. We propose the following generalization of Conjecture 1.1.
$\psi$ as above. We propose the following generalization of Conjecture 1.1.
Conjecture 6.3 Let ![]() $X_{F}$ be a K-semistable Fano variety defined over a number field
$X_{F}$ be a K-semistable Fano variety defined over a number field ![]() $F$. Then
$F$. Then
where ![]() $\psi _{\mathrm {FS}}$ denotes the volume-normalized Fubini–Study metric
$\psi _{\mathrm {FS}}$ denotes the volume-normalized Fubini–Study metric ![]() $\psi _{\mathrm {FS}}$ on
$\psi _{\mathrm {FS}}$ on ![]() $-K_{\mathbb {P}^{n}}$. Equivalently, for any model
$-K_{\mathbb {P}^{n}}$. Equivalently, for any model ![]() $(\mathcal {X},\mathcal {L})$ and continuous psh metric
$(\mathcal {X},\mathcal {L})$ and continuous psh metric ![]() $\psi$, normalized so that
$\psi$, normalized so that ![]() $\widehat {\deg }\pi _{*}(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)=0,$
$\widehat {\deg }\pi _{*}(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)=0,$
Moreover, equality holds if and only if ![]() $(\mathcal {X},\mathcal {L})$ is isomorphic to
$(\mathcal {X},\mathcal {L})$ is isomorphic to ![]() $(\mathbb {P}_{\mathcal {O}_{F}}^{n},-\mathcal {K}_{\mathbb {P}_{\mathcal {O}_{F}}^{n}}+\pi ^{*}M)$ for some line bundle
$(\mathbb {P}_{\mathcal {O}_{F}}^{n},-\mathcal {K}_{\mathbb {P}_{\mathcal {O}_{F}}^{n}}+\pi ^{*}M)$ for some line bundle ![]() $M\rightarrow \mathrm {Spec}{\mathcal {O}_{F}}$ and
$M\rightarrow \mathrm {Spec}{\mathcal {O}_{F}}$ and ![]() $\psi$ coincides with
$\psi$ coincides with ![]() $\psi _{\mathrm {FS}},$ up to the action of an automorphism of
$\psi _{\mathrm {FS}},$ up to the action of an automorphism of ![]() $\mathbb {P}^{n}$.
$\mathbb {P}^{n}$.
Note that, in general, ![]() $\mathcal {D}_{(\mathcal {X},\mathcal {L})}(\psi )=\mathcal {D}_{(\mathcal {X},\mathcal {L}+\pi ^{*}M)}(\psi )$ for any line bundle
$\mathcal {D}_{(\mathcal {X},\mathcal {L})}(\psi )=\mathcal {D}_{(\mathcal {X},\mathcal {L}+\pi ^{*}M)}(\psi )$ for any line bundle ![]() $M\rightarrow \mathrm {Spec}{\mathcal {O}_{F}.}$ We expect – inspired by Odaka's conjecture discussed in § 1.4 – that any integral model
$M\rightarrow \mathrm {Spec}{\mathcal {O}_{F}.}$ We expect – inspired by Odaka's conjecture discussed in § 1.4 – that any integral model ![]() $(\mathcal {X},\mathcal {L})$ which is globally K-semistable realizes the infimum defining the invariant
$(\mathcal {X},\mathcal {L})$ which is globally K-semistable realizes the infimum defining the invariant ![]() $\mathcal {D}(X_{F})$.
$\mathcal {D}(X_{F})$.
Next, given a polarized scheme ![]() $(\mathcal {X},\mathcal {L})$ over a number field
$(\mathcal {X},\mathcal {L})$ over a number field ![]() $F,$ we will, as in the case
$F,$ we will, as in the case ![]() $F=\mathbb {Q},$ denote by
$F=\mathbb {Q},$ denote by ![]() $\mathcal {M}_{(\mathcal {X},\mathcal {L})}(\psi )$ the arithmetic Mabuchi functional defined by the intersection-theoretic expression in formula (5.1). In general, the following inequality between the arithmetic Mabuchi functional and the arithmetic Ding functional holds, showing, in particular, that Conjecture 6.3 implies Conjecture 1.6 concerning Odaka's modular invariant. The inequality can be viewed as an arithmetic analogy of the inequality for test configurations in [Reference BermanBer16, Lemma 3.10].
$\mathcal {M}_{(\mathcal {X},\mathcal {L})}(\psi )$ the arithmetic Mabuchi functional defined by the intersection-theoretic expression in formula (5.1). In general, the following inequality between the arithmetic Mabuchi functional and the arithmetic Ding functional holds, showing, in particular, that Conjecture 6.3 implies Conjecture 1.6 concerning Odaka's modular invariant. The inequality can be viewed as an arithmetic analogy of the inequality for test configurations in [Reference BermanBer16, Lemma 3.10].
Proposition 6.4 If ![]() $(\mathcal {X},\mathcal {L})$ is a normal polarized model of
$(\mathcal {X},\mathcal {L})$ is a normal polarized model of ![]() $(X,-K_{X}\!)$ over
$(X,-K_{X}\!)$ over ![]() $\mathrm {Spec}{\mathcal {O}_{F}}$ which is
$\mathrm {Spec}{\mathcal {O}_{F}}$ which is ![]() $\mathbb {Q}$-Gorenstein, then
$\mathbb {Q}$-Gorenstein, then
with equality if and only if ![]() $\psi$ is a Kähler–Einstein metric and
$\psi$ is a Kähler–Einstein metric and ![]() $\mathcal {L}$ is isomorphic to
$\mathcal {L}$ is isomorphic to ![]() $-\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\otimes \pi ^{*}M$ for some line bundle
$-\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\otimes \pi ^{*}M$ for some line bundle ![]() $M\!$ over
$M\!$ over ![]() $\mathrm {Spec}{\mathcal {O}_{F}}$.
$\mathrm {Spec}{\mathcal {O}_{F}}$.
Proof. To simplify the notation we assume that ![]() $r=1$ (but the proof in the general case is essentially the same). It follows directly from the definitions that we need to prove that
$r=1$ (but the proof in the general case is essentially the same). It follows directly from the definitions that we need to prove that
with equality if and only if the conditions in the proposition hold. Observe that the left-hand side above is invariant when ![]() $\mathcal {L}$ is replaced by
$\mathcal {L}$ is replaced by ![]() $\mathcal {L}+\pi ^{*}M,$ where
$\mathcal {L}+\pi ^{*}M,$ where ![]() $M$ is any line bundle over
$M$ is any line bundle over ![]() $\mathrm {Spec}{\mathcal {O}_{F}.}$ Hence, we may as well assume that
$\mathrm {Spec}{\mathcal {O}_{F}.}$ Hence, we may as well assume that ![]() $\pi _{*}(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)$ admits a global regular section
$\pi _{*}(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)$ admits a global regular section ![]() $s$ that is non-vanishing over the generic fiber. Now, by the restriction formula for arithmetic intersection numbers [Reference Bost, Gillet and SouléBGS94, Proposition 2.3.1],
$s$ that is non-vanishing over the generic fiber. Now, by the restriction formula for arithmetic intersection numbers [Reference Bost, Gillet and SouléBGS94, Proposition 2.3.1],
where ![]() $(s=0)$ denotes the subscheme of
$(s=0)$ denotes the subscheme of ![]() $\mathcal {X}$ cut out by
$\mathcal {X}$ cut out by ![]() $s$. By Jensen's inequality,
$s$. By Jensen's inequality,
 \begin{align} \int_{X(\mathbb{C})}\log\biggl(\frac{MA(\psi)}{|s|^{2}e^{-\psi}}\biggr)MA(\psi)&\geq -\frac{1}{2}\sum_{\sigma}\log\int_{X_{\sigma}}|s|^{2}e^{-\psi}\nonumber\\ &=\widehat{\deg}\pi_{*}(\mathcal{L}+\mathcal{K}_{\mathcal{X}/\mathrm{Spec}{\mathcal{O}_{F}}}\!)-\sum_{\mathfrak{p}}\mathrm{ord}_{\mathfrak{p}}(s)\log\!|\mathfrak{p}|. \end{align}
\begin{align} \int_{X(\mathbb{C})}\log\biggl(\frac{MA(\psi)}{|s|^{2}e^{-\psi}}\biggr)MA(\psi)&\geq -\frac{1}{2}\sum_{\sigma}\log\int_{X_{\sigma}}|s|^{2}e^{-\psi}\nonumber\\ &=\widehat{\deg}\pi_{*}(\mathcal{L}+\mathcal{K}_{\mathcal{X}/\mathrm{Spec}{\mathcal{O}_{F}}}\!)-\sum_{\mathfrak{p}}\mathrm{ord}_{\mathfrak{p}}(s)\log\!|\mathfrak{p}|. \end{align}
Hence, decomposing the subscheme ![]() $(s=0)$ of
$(s=0)$ of ![]() $\mathcal {X}$ as a sum of effective divisors
$\mathcal {X}$ as a sum of effective divisors ![]() $E_{\mathfrak {p}},$ where
$E_{\mathfrak {p}},$ where ![]() $E_{\mathfrak {p}}$ is supported on the fiber
$E_{\mathfrak {p}}$ is supported on the fiber ![]() $\mathcal {X}_{\mathfrak {p}}$ of
$\mathcal {X}_{\mathfrak {p}}$ of ![]() $\mathcal {X}$ over
$\mathcal {X}$ over ![]() $\mathfrak {p},$
$\mathfrak {p},$
 \[ \frac{1}{L^{n}}\bigl(\overline{\mathcal{L}}+\overline{\mathcal{K}}\bigr) \cdot\overline{\mathcal{L}}^{n}\geq\frac{1}{L^{n}}(s=0)\cdot\overline{\mathcal{L}}^{n} -\sum_{\mathfrak{p}}\mathrm{ord}_{\mathfrak{p}}(s)\log\!|\mathfrak{p}| =\biggl(\frac{1}{L^{n}}\mathcal{L}_{|\mathcal{X}_{\mathfrak{p}}}^{n}\cdot E_{\mathfrak{p}}-\sum_{\mathfrak{p}}\mathrm{ord}_{\mathfrak{p}}(s)\biggr)\log\!|\mathfrak{p}|, \]
\[ \frac{1}{L^{n}}\bigl(\overline{\mathcal{L}}+\overline{\mathcal{K}}\bigr) \cdot\overline{\mathcal{L}}^{n}\geq\frac{1}{L^{n}}(s=0)\cdot\overline{\mathcal{L}}^{n} -\sum_{\mathfrak{p}}\mathrm{ord}_{\mathfrak{p}}(s)\log\!|\mathfrak{p}| =\biggl(\frac{1}{L^{n}}\mathcal{L}_{|\mathcal{X}_{\mathfrak{p}}}^{n}\cdot E_{\mathfrak{p}}-\sum_{\mathfrak{p}}\mathrm{ord}_{\mathfrak{p}}(s)\biggr)\log\!|\mathfrak{p}|, \]
using, again, the restriction formula in the last equality. Since ![]() $\mathrm {ord}_{\mathfrak {p}}(s)\geq 0,$ we can express
$\mathrm {ord}_{\mathfrak {p}}(s)\geq 0,$ we can express ![]() $E_{\mathfrak {p}}=E'_{\mathfrak {p}}+\mathrm {ord}_{\mathfrak {p}}(s)\mathcal {X}_{\mathfrak {p}}$ for an effective divisor
$E_{\mathfrak {p}}=E'_{\mathfrak {p}}+\mathrm {ord}_{\mathfrak {p}}(s)\mathcal {X}_{\mathfrak {p}}$ for an effective divisor ![]() $E'_{\mathfrak {p}},$ giving
$E'_{\mathfrak {p}},$ giving
Finally, equality holds in inequality (6.6) if and only if ![]() $MA(\psi )$ is proportional to
$MA(\psi )$ is proportional to ![]() $|s|^{2}e^{-\psi }$ for all
$|s|^{2}e^{-\psi }$ for all ![]() $X_{\sigma }$, i.e. if and only if
$X_{\sigma }$, i.e. if and only if ![]() $\psi$ is Kähler–Einstein. Moreover, since
$\psi$ is Kähler–Einstein. Moreover, since ![]() $\mathcal {L}$ is relatively ample the right-hand side in the last inequality above vanishes if and only if
$\mathcal {L}$ is relatively ample the right-hand side in the last inequality above vanishes if and only if ![]() $E'_{\mathfrak {p}}$ is the zero-divisor for all
$E'_{\mathfrak {p}}$ is the zero-divisor for all ![]() $\mathfrak {p}$, i.e. if and only if (
$\mathfrak {p}$, i.e. if and only if (![]() $s=0)$ is a linear combination of fibers
$s=0)$ is a linear combination of fibers ![]() $\mathcal {X}_{\mathfrak {p}}$ and thus
$\mathcal {X}_{\mathfrak {p}}$ and thus ![]() $\mathcal {L}+\mathcal {K}$ is isomorphic to
$\mathcal {L}+\mathcal {K}$ is isomorphic to ![]() $\pi ^{*}M$ for some line bundle
$\pi ^{*}M$ for some line bundle ![]() $M$ over
$M$ over ![]() $\mathrm {Spec}{\mathcal {O}_{F}.}$
$\mathrm {Spec}{\mathcal {O}_{F}.}$
6.3 Comparison with bounds on Bost–Zhang normalized heights
The normalized arithmetic Ding functional ![]() $\mathcal {\hat {D}}_{(\mathcal {X},\mathcal {L})}$ is reminiscent of Bost's normalized height
$\mathcal {\hat {D}}_{(\mathcal {X},\mathcal {L})}$ is reminiscent of Bost's normalized height![]() $h_{\mathrm {norm}},$ introduced in [Reference BostBos96] in the general setup of polarized variety
$h_{\mathrm {norm}},$ introduced in [Reference BostBos96] in the general setup of polarized variety ![]() $(X_{F},L_{F})$ defined over a number field
$(X_{F},L_{F})$ defined over a number field ![]() $F$:
$F$:
assuming that the rank ![]() $N$ of the vector bundle
$N$ of the vector bundle ![]() $\pi _{*}\mathcal {L}\rightarrow \mathrm {Spec}\mathcal {O}_{F}$ is non-zero and
$\pi _{*}\mathcal {L}\rightarrow \mathrm {Spec}\mathcal {O}_{F}$ is non-zero and ![]() $\pi _{*}(\mathcal {X},\mathcal {L})$ is endowed with the
$\pi _{*}(\mathcal {X},\mathcal {L})$ is endowed with the ![]() $L^{2}$-norm induced by the continuous psh metrics
$L^{2}$-norm induced by the continuous psh metrics ![]() $\psi _{\sigma }$ on
$\psi _{\sigma }$ on ![]() $L_{\sigma }$ and the volume forms
$L_{\sigma }$ and the volume forms ![]() $MA(\psi _{\sigma })$ on
$MA(\psi _{\sigma })$ on ![]() $X_{\sigma }$ (defined by formula (4.3)). When
$X_{\sigma }$ (defined by formula (4.3)). When ![]() $L_{F}$ is very ample it is shown in [Reference BostBos96] that the functional
$L_{F}$ is very ample it is shown in [Reference BostBos96] that the functional ![]() $h_{\mathrm {norm}}(\mathcal {L},\cdot )$ is bounded from below if and only if the Chow point of
$h_{\mathrm {norm}}(\mathcal {L},\cdot )$ is bounded from below if and only if the Chow point of ![]() $(X_{F},L_{F})$ is semistable with respect to the action of the group
$(X_{F},L_{F})$ is semistable with respect to the action of the group ![]() $GL(N,F)$ on the Chow variety (in the sense of geometric invariant theory). More precisely, it is shown in [Reference BostBos96] that the semistability in question is equivalent to a lower bound on Bost's intrinsic normalized height of
$GL(N,F)$ on the Chow variety (in the sense of geometric invariant theory). More precisely, it is shown in [Reference BostBos96] that the semistability in question is equivalent to a lower bound on Bost's intrinsic normalized height of ![]() $(X_{F},L_{F})$:
$(X_{F},L_{F})$:
where the infimum runs over all models ![]() $(\mathcal {X},\mathcal {L})$ and metrics
$(\mathcal {X},\mathcal {L})$ and metrics ![]() $\psi$ as above. In fact, by [Reference BostBos96, Proposition 2.1] and [Reference ZhangZha96, Theorem 4.4] the Chow semistability in question is equivalent to the following explicit lower bound:
$\psi$ as above. In fact, by [Reference BostBos96, Proposition 2.1] and [Reference ZhangZha96, Theorem 4.4] the Chow semistability in question is equivalent to the following explicit lower bound:
 \begin{equation} h_{\mathrm{norm}}(\mathcal{L},\psi)\geq-\frac{1}{2}\sum_{n=1}^{N+1}\sum_{m=1}^{n}\frac{1}{m}-\frac{1}{2}\log N \end{equation}
\begin{equation} h_{\mathrm{norm}}(\mathcal{L},\psi)\geq-\frac{1}{2}\sum_{n=1}^{N+1}\sum_{m=1}^{n}\frac{1}{m}-\frac{1}{2}\log N \end{equation}(moreover, it is conjectured in [Reference ZhangZha96] that the first term in the right-hand side above may be replaced by 0).
In this setup the role of the normalization ![]() $\widehat {\deg }\pi _{*}(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)=0$ in Conjecture 6.3 is thus played by the normalization
$\widehat {\deg }\pi _{*}(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)=0$ in Conjecture 6.3 is thus played by the normalization ![]() $\widehat {\deg }\pi _{*}\mathcal {L}=0$. However, in contrast to Conjecture 6.3, the lower bound (6.7) on
$\widehat {\deg }\pi _{*}\mathcal {L}=0$. However, in contrast to Conjecture 6.3, the lower bound (6.7) on ![]() $h_{\mathrm {norm }}(\mathcal {L},\psi )$ corresponds to a lower bound on
$h_{\mathrm {norm }}(\mathcal {L},\psi )$ corresponds to a lower bound on ![]() $(\mathcal {L},\psi )^{n+1}$ for any normalized metric. Note also that one virtue of the normalization condition in Conjecture 6.3 is that it is comparatively explicit, since
$(\mathcal {L},\psi )^{n+1}$ for any normalized metric. Note also that one virtue of the normalization condition in Conjecture 6.3 is that it is comparatively explicit, since ![]() $\pi _{*}(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)$ has rank
$\pi _{*}(\mathcal {L}+\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}\!)$ has rank ![]() $1$ (so that formula (6.3) applies, showing that it is enough to assume that the volume forms
$1$ (so that formula (6.3) applies, showing that it is enough to assume that the volume forms ![]() $|s_{r}|^{2/r}e^{-\psi _{\sigma }}$ on
$|s_{r}|^{2/r}e^{-\psi _{\sigma }}$ on ![]() $X_{\sigma }$ are normalized). Another advantage of this normalization condition is that it applies to any continuous metric
$X_{\sigma }$ are normalized). Another advantage of this normalization condition is that it applies to any continuous metric ![]() $\psi$ (at the cost of replacing
$\psi$ (at the cost of replacing ![]() $(\mathcal {L},\psi )^{n+1}$ with the
$(\mathcal {L},\psi )^{n+1}$ with the ![]() $\chi$-arithmetic volume of
$\chi$-arithmetic volume of ![]() $\mathcal {L},$ as in Theorem 2.5).
$\mathcal {L},$ as in Theorem 2.5).
Finally, we recall that when ![]() $\mathcal {L}$ is replaced by
$\mathcal {L}$ is replaced by ![]() $k\mathcal {L}$ for a large positive integer
$k\mathcal {L}$ for a large positive integer ![]() $k$ it follows from [Reference OdakaOda18, Theorem 3.7] that there exist constants
$k$ it follows from [Reference OdakaOda18, Theorem 3.7] that there exist constants ![]() $a>0$ and
$a>0$ and ![]() $b$ (depending only on
$b$ (depending only on ![]() $(X_{F},L_{F})$) such that
$(X_{F},L_{F})$) such that
as ![]() $k\rightarrow \infty,$ where
$k\rightarrow \infty,$ where ![]() $N_{k}$ denotes the rank of
$N_{k}$ denotes the rank of ![]() $H^{0}(\mathcal {X},k\mathcal {L})$ which diverges as
$H^{0}(\mathcal {X},k\mathcal {L})$ which diverges as ![]() $k\rightarrow \infty$. Unfortunately, the diverging term
$k\rightarrow \infty$. Unfortunately, the diverging term ![]() $a\log N_{k}$ makes it impossible to infer lower bounds on
$a\log N_{k}$ makes it impossible to infer lower bounds on ![]() $\mathcal {M}_{(\mathcal {X},\mathcal {L})}(\psi )$ from lower bounds on
$\mathcal {M}_{(\mathcal {X},\mathcal {L})}(\psi )$ from lower bounds on ![]() $h_{\mathrm {norm}}(k\mathcal {L})$. Since
$h_{\mathrm {norm}}(k\mathcal {L})$. Since ![]() $\mathcal {M}_{(\mathcal {X},\mathcal {L})}(\psi )$ coincides with
$\mathcal {M}_{(\mathcal {X},\mathcal {L})}(\psi )$ coincides with ![]() $\mathcal {D}_{(\mathcal {X},\mathcal {L})}(\psi )$ when
$\mathcal {D}_{(\mathcal {X},\mathcal {L})}(\psi )$ when ![]() $\mathcal {L}$ equals
$\mathcal {L}$ equals ![]() $-\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}$ this means that Conjecture 6.3 cannot be deduced from bounds of the form (6.7) by letting
$-\mathcal {K}_{\mathcal {X}/\mathrm {Spec}{\mathcal {O}_{F}}}$ this means that Conjecture 6.3 cannot be deduced from bounds of the form (6.7) by letting ![]() $k$ (and hence
$k$ (and hence ![]() $N)$ tend to infinity.
$N)$ tend to infinity.
6.4 Comparison with Odaka's and Faltings’s modular heights
Finally, let us compare our normalizations of the arithmetic Mabuchi functional with those of Odaka [Reference OdakaOda20] and Faltings [Reference FaltingsFal83a]. First of all, our multiplicative normalization for the arithmetic Mabuchi functional ![]() $\mathcal {M}_{(\mathcal {X},\mathcal {L})}$ (formula (1.6)) is made so that
$\mathcal {M}_{(\mathcal {X},\mathcal {L})}$ (formula (1.6)) is made so that ![]() $\pm \mathcal {M}_{(\mathcal {X},\pm K_{\mathcal {X}})}=(\pm \mathcal {K}_{\mathcal {X}})^{n+1}/(n+1)$. Moreover, as discussed in § 1.4.1, we are employing the metric on
$\pm \mathcal {M}_{(\mathcal {X},\pm K_{\mathcal {X}})}=(\pm \mathcal {K}_{\mathcal {X}})^{n+1}/(n+1)$. Moreover, as discussed in § 1.4.1, we are employing the metric on ![]() $-K_{X\!}$ induced by the normalized volume form
$-K_{X\!}$ induced by the normalized volume form ![]() $\omega ^{n}/L^{n}$ of the Kähler form
$\omega ^{n}/L^{n}$ of the Kähler form ![]() $\omega$ defined by a given metric
$\omega$ defined by a given metric ![]() $\psi$ on
$\psi$ on ![]() $\mathcal {L}$ with positive curvature (i.e.
$\mathcal {L}$ with positive curvature (i.e. ![]() $\omega =dd^{c}\psi )$. Comparing with Odaka's arithmetic Mabuchi functional, which we shall denote by
$\omega =dd^{c}\psi )$. Comparing with Odaka's arithmetic Mabuchi functional, which we shall denote by ![]() $\mathcal {M}_{(\mathcal {X},\mathcal {L})}^{(O)}(\psi ),$ thus yields
$\mathcal {M}_{(\mathcal {X},\mathcal {L})}^{(O)}(\psi ),$ thus yields
In the case that ![]() $\mathcal {X}$ is an abelian variety it was shown in [Reference OdakaOda20] that the infimum of Odaka's arithmetic Mabuchi functional over all metrics on
$\mathcal {X}$ is an abelian variety it was shown in [Reference OdakaOda20] that the infimum of Odaka's arithmetic Mabuchi functional over all metrics on ![]() $\mathcal {L}$ with positive curvature coincides with Faltings’s (modular) height [Reference FaltingsFal83a], up to a multiplicative and an additive constant depending on
$\mathcal {L}$ with positive curvature coincides with Faltings’s (modular) height [Reference FaltingsFal83a], up to a multiplicative and an additive constant depending on ![]() $L^{n}$. Here we note that our normalizations are consistent with those of Faltings.
$L^{n}$. Here we note that our normalizations are consistent with those of Faltings.
Proposition 6.5 Let ![]() $\mathcal {X}$ be a projective and flat scheme over
$\mathcal {X}$ be a projective and flat scheme over ![]() $\mathbb {Z}$ and assume that
$\mathbb {Z}$ and assume that ![]() $\mathcal {K_{\mathcal {X}}}$ is trivial. For any relatively ample line bundle
$\mathcal {K_{\mathcal {X}}}$ is trivial. For any relatively ample line bundle ![]() $\mathcal {L}$ over
$\mathcal {L}$ over ![]() $\mathcal {X\!}$,
$\mathcal {X\!}$,
 \begin{equation} \inf_{\psi}\frac{1}{L^{n}/n!}\mathcal{M}_{(\mathcal{X},\mathcal{L})}(\psi)=-\frac{1}{2[\mathbb{F}:\mathbb{Q}]}\log\frac{1}{2^{n}}\left|\int_{X(\mathbb{C})}\Omega\wedge\bar{\Omega}\right|, \end{equation}
\begin{equation} \inf_{\psi}\frac{1}{L^{n}/n!}\mathcal{M}_{(\mathcal{X},\mathcal{L})}(\psi)=-\frac{1}{2[\mathbb{F}:\mathbb{Q}]}\log\frac{1}{2^{n}}\left|\int_{X(\mathbb{C})}\Omega\wedge\bar{\Omega}\right|, \end{equation}
where ![]() $\Omega$ is a generator of
$\Omega$ is a generator of ![]() $H^{0}(\mathcal {X},\mathcal {K}_{\mathcal {X}})$ and the infimum ranges over all psh metrics
$H^{0}(\mathcal {X},\mathcal {K}_{\mathcal {X}})$ and the infimum ranges over all psh metrics ![]() $\psi$ on
$\psi$ on ![]() $\mathcal {L}$ and
$\mathcal {L}$ and ![]() $V:=L^{n}/n!$.
$V:=L^{n}/n!$.
Proof. This is essentially equivalent to [Reference OdakaOda20, Theorem 2.11], using relation (6.9). In any case, in order to verify that all normalizations are consistent we provide a simple direct proof. Assume, to simplify the notation, that ![]() $\mathbb {F}=\mathbb {Q}$. Recall that Faltings’s modular height [Reference FaltingsFal83a] is defined as the arithmetic degree of
$\mathbb {F}=\mathbb {Q}$. Recall that Faltings’s modular height [Reference FaltingsFal83a] is defined as the arithmetic degree of ![]() $\pi _{*}(\mathcal {X},K_{\mathcal {X}}),$ with respect to the
$\pi _{*}(\mathcal {X},K_{\mathcal {X}}),$ with respect to the ![]() $L^{2}$-metric on
$L^{2}$-metric on ![]() $H^{0}(X,K_{X}\!)$ defined by
$H^{0}(X,K_{X}\!)$ defined by ![]() $\Vert \Omega \Vert ^{2}:=({1}/{2^{n}})|\int _{X(\mathbb {C})}\Omega \wedge \bar {\Omega }|$. This is precisely the right-hand side in formula (6.10). As for the left-hand side, it is given by
$\Vert \Omega \Vert ^{2}:=({1}/{2^{n}})|\int _{X(\mathbb {C})}\Omega \wedge \bar {\Omega }|$. This is precisely the right-hand side in formula (6.10). As for the left-hand side, it is given by
(as follows readily from the definitions, just as in formula (6.5)). Now, by Jensen's inequality this expression is minimal precisely when the two probability measures ![]() $(dd^{c}\psi )^{n}/Vn!$ and
$(dd^{c}\psi )^{n}/Vn!$ and ![]() $2^{-n}i^{n^{2}/2}\Omega \wedge \bar {\Omega }/\Vert \Omega \Vert ^{2}$ coincide, which, equivalently, means that
$2^{-n}i^{n^{2}/2}\Omega \wedge \bar {\Omega }/\Vert \Omega \Vert ^{2}$ coincide, which, equivalently, means that ![]() $dd^{c}\psi$ is a Kähler–Einstein metric. By the Calabi–Yau theorem such a metric exists for any given ample
$dd^{c}\psi$ is a Kähler–Einstein metric. By the Calabi–Yau theorem such a metric exists for any given ample ![]() $L,$ which concludes the proof.
$L,$ which concludes the proof.
The previous proposition has the following consequence, when combined with well-known properties of Faltings’s modular height of abelian varieties (cf. the discussion in relation to [Reference OdakaOda20, Theorem 2.11] and [Reference OdakaOda20, § 2.3.2]). Consider a polarized abelian variety ![]() $(X_{\mathbb {F}_{0}},L_{\mathbb {F}_{0}})$ defined over a given number field
$(X_{\mathbb {F}_{0}},L_{\mathbb {F}_{0}})$ defined over a given number field ![]() $\mathbb {F}_{0}$. Then the infimum of
$\mathbb {F}_{0}$. Then the infimum of ![]() $\mathrm {vol}(L)^{-1}\mathcal {M}_{(\mathcal {X},\mathcal {L})}$ over all metrics, finite field extensions
$\mathrm {vol}(L)^{-1}\mathcal {M}_{(\mathcal {X},\mathcal {L})}$ over all metrics, finite field extensions ![]() $\mathbb {F},$ models over
$\mathbb {F},$ models over ![]() $\mathcal {O}_{\mathbb {F}}$ and positively curved metrics on
$\mathcal {O}_{\mathbb {F}}$ and positively curved metrics on ![]() $L\rightarrow X_{\mathbb {F}}(\mathbb {C})$ is attained at any semistable reduction of the Néron model
$L\rightarrow X_{\mathbb {F}}(\mathbb {C})$ is attained at any semistable reduction of the Néron model ![]() $\mathcal {X}$ of
$\mathcal {X}$ of ![]() $X_{\mathbb {F}},$ when
$X_{\mathbb {F}},$ when ![]() $L$ is endowed with a Kähler–Einstein metric. Moreover, in the particular case of elliptic curves it was observed in [Reference DeligneDel85, p. 29] that the minimal value of the aforementioned infimum over all
$L$ is endowed with a Kähler–Einstein metric. Moreover, in the particular case of elliptic curves it was observed in [Reference DeligneDel85, p. 29] that the minimal value of the aforementioned infimum over all ![]() $X_{\mathbb {F}}$ is attained at the semistable reduction of the Néron model
$X_{\mathbb {F}}$ is attained at the semistable reduction of the Néron model ![]() $\mathcal {X}_{0}$ of any elliptic curve with vanishing
$\mathcal {X}_{0}$ of any elliptic curve with vanishing ![]() $j$-invariant (
$j$-invariant (![]() $\mathcal {X}_{0}$ is uniquely determined for any sufficiently large field extension). Thus the role of
$\mathcal {X}_{0}$ is uniquely determined for any sufficiently large field extension). Thus the role of ![]() $\mathcal {X}_{0}$ among all models of elliptic curves is somewhat analogous to the role of
$\mathcal {X}_{0}$ among all models of elliptic curves is somewhat analogous to the role of ![]() $\mathbb {P}_{\mathbb {Z}}^{n}$ in Conjectures 1.1 and 1.6. However, it should be stressed that in the setup of Fano varieties the choice of multiplicative normalization is crucial. Indeed, while
$\mathbb {P}_{\mathbb {Z}}^{n}$ in Conjectures 1.1 and 1.6. However, it should be stressed that in the setup of Fano varieties the choice of multiplicative normalization is crucial. Indeed, while ![]() $\mathbb {P}_{\mathbb {Z}}^{n}$ minimizes
$\mathbb {P}_{\mathbb {Z}}^{n}$ minimizes ![]() $\mathcal {M}_{(\mathcal {X},-\mathcal {K}_{\mathcal {X}})}(\psi _{\mathrm {KE}})$ over the canonical toric integral models of all K-semistable toric Fano varieties
$\mathcal {M}_{(\mathcal {X},-\mathcal {K}_{\mathcal {X}})}(\psi _{\mathrm {KE}})$ over the canonical toric integral models of all K-semistable toric Fano varieties ![]() $X\!$ (assuming that
$X\!$ (assuming that ![]() $n\leq 6)$ it does not minimize
$n\leq 6)$ it does not minimize ![]() $\mathrm {vol}(-K_{X}\!)^{-1}\mathcal {M}_{(\mathcal {X},-\mathcal {K}_{\mathcal {X}})}(\psi _{\mathrm {KE}})$. In fact, for all we know it could actually be the case that
$\mathrm {vol}(-K_{X}\!)^{-1}\mathcal {M}_{(\mathcal {X},-\mathcal {K}_{\mathcal {X}})}(\psi _{\mathrm {KE}})$. In fact, for all we know it could actually be the case that ![]() $\mathrm {vol}(-K_{X}\!)^{-1}\mathcal {M}_{(\mathcal {X},-\mathcal {K}_{\mathcal {X}})}(\psi _{\mathrm {KE}})$ is maximal on
$\mathrm {vol}(-K_{X}\!)^{-1}\mathcal {M}_{(\mathcal {X},-\mathcal {K}_{\mathcal {X}})}(\psi _{\mathrm {KE}})$ is maximal on ![]() $\mathbb {P}_{\mathbb {Z}}^{n}$. For example, this turns out to be the case in the more general setup of Fano orbifolds (not assumed toric) when
$\mathbb {P}_{\mathbb {Z}}^{n}$. For example, this turns out to be the case in the more general setup of Fano orbifolds (not assumed toric) when ![]() $X\!$ has relative dimension
$X\!$ has relative dimension ![]() $1$ (a proof will appear in a separate publication).
$1$ (a proof will appear in a separate publication).
Acknowledgements
We are grateful to Bo Berndtsson, Dennis Eriksson, Gerard Freixas i Montplet, Benjamin Nill, Yuji Odaka, Per Salberger, Chenyang Xu and Ziquan Zhuang for illuminating discussions/comments and, in particular, to Alexander Kasprzyk for updating the database [Reference ØbroØbr07]. We are also grateful to the refere for very helpful comments.
Conflicts of interest
None.
Financial support
This work was supported by grants from the Knut and Alice Wallenberg Foundation, the Göran Gustafsson Foundation and the Swedish Research Council.
Data availability
The database of smooth toric Fano varieties of dimension at most six (http://www.grdb.co.uk/forms/toricsmooth) is used in the proof of Theorem 1.2. This data is provided by Mikkel Obro.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.