Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T07:49:58.010Z Has data issue: false hasContentIssue false
  • English
  • Français

FOUR-MANIFOLDS WITH POSITIVE CURVATURE

Part of: Global differential geometry

Published online by Cambridge University Press:  06 April 2020

R. DIÓGENES ,
E. RIBEIRO  and
E. RUFINO
R. DIÓGENES
Affiliation:
UNILAB, Instituto de Ciências Exatas e da Natureza, Campus dos Palmares, ROD. CE 060, KM 51, 62.785-000 Acarape, CE, Brazil e-mail: [email protected]
E. RIBEIRO
Affiliation:
Departamento de Matemática, Universidade Federal do Ceará - UFC, CAMPUS do Pici, Av. Humberto Monte, Bloco 914, 60455-760Fortaleza, CE, Brazil e-mail: [email protected]
E. RUFINO
Affiliation:
Departamento de Matemática, Universidade Federal de Roraima - UFRR, Campus Paricarana, Av. CAP. Ene Garcez, 2413, 69310-000Boa Vista, RR, Brazil e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note, we prove that a four-dimensional compact oriented half-conformally flat Riemannian manifold M4 is topologically 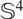$\mathbb{S}^{4}$ or 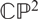$\mathbb{C}\mathbb{P}^{2}$ , provided that the sectional curvatures all lie in the interval 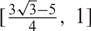$\left[ {{{3\sqrt {3 - 5} } \over 4}, 1} \right]$ In addition, we use the notion of biorthogonal (sectional) curvature to obtain a pinching condition which guarantees that a four-dimensional compact manifold is homeomorphic to a connected sum of copies of the complex projective plane or the 4-sphere.

MSC classification

Primary: 53C25: Special Riemannian manifolds (Einstein, Sasakian, etc.) 53C20: Global Riemannian geometry, including pinching 53C21: Methods of Riemannian geometry, including PDE methods; curvature restrictions
Secondary: 53C65: Integral geometry
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 2 , May 2021 , pp. 245 - 257
Copyright
© Glasgow Mathematical Journal Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

E. Ribeiro Jr. was partially supported by grants from CNPq/Brazil (Grant: 303091/2015-0), PRONEX-FUNCAP/CNPq/Brazil, and CAPES/Brazil – Finance Code 001.

E. Rufino was partially supported by CAPES/Brazil.

References

Berger, M., Les variétés Riemenniennes $1/4$ -pincées, Ann. Scuola Norm. Sup. Pisa 14 (1960), 161–170.Google Scholar
Berger, M., Sur quelques variétés Riemenniennes suffisament pincées, Bull. Soc. Math. France 88 (1960), 57–71.CrossRefGoogle Scholar
Besse, A., Einstein manifolds (Springer-Verlag, New York, 2008).Google Scholar
Bettiol, R., Positive biorthogonal curvature on ${S^2} \times {S^2}$ , Proc. Amer. Math. Soc. 142 (2014), 4341–4353.CrossRefGoogle Scholar
Bettiol, R., Four-dimensional manifolds with positive biorthogonal curvature, Asian J. Math. 21 (2017), 391–396.CrossRefGoogle Scholar
Bourguignon, J., La conjecture de Hopf sur ${S^2} \times {S^2}$ Geometrie Riemannienne en dimension 4, Seminaire Arthur Besse, CEDIC Paris, 1981, 347–355.Google Scholar
Brendle, S. and Schoen, R., Curvature, sphere theorems, and the Ricci flow, Bull. Amer. Math. Soc. 48 (2010), 1–32.CrossRefGoogle Scholar
Brendle, S. and Schoen, R., Manifolds with $1/4$ -pinched curvature are space forms, J. Amer. Math. Soc. 22 (2009), 287–307.Google Scholar
Cao, X. and Tran, H., Einstein four manifolds with pinched sectional curvature, Adv. Math. 335 (2018), 322–342.Google Scholar
Cao, X. and Tran, H., Four-manifolds of pinched sectional curvature. Arxiv: 1809.05158v2 [math.DG] (2019).Google Scholar
Costa, E. and Ribeiro, E., Four-dimensional compact manifolds with nonnegative biorthogonal curvature, Michigan Math. J. 63 (2014), 673–688.Google Scholar
Cui, Q. and Sun, L., On the topology and rigidity of four-dimensional Einstein manifolds. Preprint (2018).Google Scholar
Diógenes, R. and Ribeiro, E. Jr., Four-dimensional manifolds with pinched positive sectional curvature, Geom. Dedicata. 200 (2019), 321–330.Google Scholar
Donaldson, K., An application of gauge theory to four dimensional topology, J. Differential Geom. 18 (1983) 279–315.Google Scholar
Freedman, M., The topology of four-dimensional manifolds, J. Differential Geom. 17 (1982), 327–454.CrossRefGoogle Scholar
Gray, A., Invariants of curvature operators of four-dimensional Riemannian manifolds, in Proceedings of 13th Biennial Seminar Canadian Mathematics Congress, vol. 2 (1972), 42–65.Google Scholar
Gursky, M., Four-manifolds with $\delta {W^ + } = 0$ and Einstein constants of the sphere, Math. Ann. 318 (2000), 417–431.CrossRefGoogle Scholar
Hulin, D., Le second nombre de Betti d’une variété riemannienne $({1 \over 4} - \varepsilon )$ -pincée de dimension 4, Annales de l’Institut Fourier. 33(2) (1983), 167–182.CrossRefGoogle Scholar
Klingenberg, W., Über Riemannsche Mannigfaltigkeiten mit positiver Krümmung, Comment. Math. Helv. 35 (1961), 47–54.CrossRefGoogle Scholar
Ko, K.-S., On 4-dimensional Einstein manifolds which are positively pinched, Korean J. Math. 3 (1995), 81–88.Google Scholar
LeBrun, C., Explicit self-fual metrics on $\Bbb{CP}^{2}\sharp\cdots\sharp\Bbb{CP}^{2}$ , J. Diff. Geom. 34 (1991), 223–253.Google Scholar
Noronha, H., Self-duality and 4-manifolds with nonnegative curvature on totally isotropic 2-planes, Michigan Math. J. 41 (1994), 3–12.CrossRefGoogle Scholar
Noronha, H., Some results on nonnegatively curved four manifods, Matemat. Contemp. 9 (1995), 153–175.Google Scholar
Petersen, P. and Tao, T., Classification of almost quarter-pinched manifolds, Proc. Amer. Math. Soc. 137 (2009), 2437–2440.CrossRefGoogle Scholar
Rauch, H., A contribution to differential geometry in the large, Ann. Math. 54 (1951), 38–55.CrossRefGoogle Scholar
Ribeiro, E. ., Rigidity of four-dimensional compact manifolds with harmonic Weyl tensor, Annali di Matematica Pura Appl. 195 (2016), 2171–2181.CrossRefGoogle Scholar
Seaman, W., Harmonic two-forms in four dimensions, Proc. Amer. Math. Soc. 112 (1991), 545–548.CrossRefGoogle Scholar
Seaman, W., On manifolds with nonnegative curvature on totally isotropic 2-planes, Trans. Amer. Math. Soc. 338 (1993), 843–855.Google Scholar
Seaman, W., Orthogonally pinched curvature tensors and aplications, Math. Scand. 69 (1991), 5–14.CrossRefGoogle Scholar
Singer, I. and Thorpe, J., The curvature of 4-dimensional spaces, in Global Analysis, Papers in Honor of K. Kodaira (Princeton, 1969), 355–365.Google Scholar
Ville, M., Les variétés Riemannienes de dimension 4 ${4 \over {19}}$ -pincées, Ann. Inst. Fourier 39 (1989), 149–154.CrossRefGoogle Scholar
Ville, M., On $1/4$ -pinched 4-dimensional Riemannian manifolds of negative curvature, Ann. Glob. Anal. Geom. 3 (1985), 329–336.CrossRefGoogle Scholar
Wu, P., A note on Einstein four-manifolds with positive curvature, J. Geom. Phys. 114 (2017) 19–22.Google Scholar