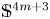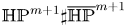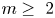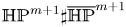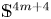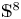1. Introduction
A Riemannian manifold ![]() $(M,g)$ is Einstein if its Ricci curvature is a constant multiple of
$(M,g)$ is Einstein if its Ricci curvature is a constant multiple of ![]() $g$:
$g$:
The metric ![]() $g$ is then called an Einstein metric and
$g$ is then called an Einstein metric and ![]() $\Lambda$ is the Einstein constant. Depending on the sign of
$\Lambda$ is the Einstein constant. Depending on the sign of ![]() $\Lambda$, we call
$\Lambda$, we call ![]() $g$ a positive Einstein (
$g$ a positive Einstein (![]() $\Lambda >0$) metric, a negative Einstein (
$\Lambda >0$) metric, a negative Einstein (![]() $\Lambda <0$) metric or a Ricci-flat (
$\Lambda <0$) metric or a Ricci-flat (![]() $\Lambda =0$) metric. A positive Einstein manifold is compact by Myers’ theorem [Reference MyersMye41].
$\Lambda =0$) metric. A positive Einstein manifold is compact by Myers’ theorem [Reference MyersMye41].
In this paper we investigate the existence of positive Einstein metrics of cohomogeneity one. A Riemannian manifold ![]() $(M, g)$ is of cohomogeneity one if a Lie group
$(M, g)$ is of cohomogeneity one if a Lie group ![]() $\mathsf {G}$ acts isometrically on
$\mathsf {G}$ acts isometrically on ![]() $M$ such that the principal orbit
$M$ such that the principal orbit ![]() $\mathsf {G}/\mathsf {K}$ is of codimension one. The first example of an inhomogeneous positive Einstein metric was constructed in [Reference PagePag78]. The metric is defined on
$\mathsf {G}/\mathsf {K}$ is of codimension one. The first example of an inhomogeneous positive Einstein metric was constructed in [Reference PagePag78]. The metric is defined on ![]() $\mathbb {CP}^{2}\sharp \overline {\mathbb {CP}}^{2}$ and is of cohomogeneity one. The result was later generalized in [Reference Bérard-BergeryBer82, Reference Koiso and SakaneKS86, Reference SakaneSak86, Reference Page and PopePP87, Reference Koiso and SakaneKS88, Reference Wang and WangWW98]. A common feature shared by positive Einstein metrics constructed in this series of works is that the principal orbits are principal
$\mathbb {CP}^{2}\sharp \overline {\mathbb {CP}}^{2}$ and is of cohomogeneity one. The result was later generalized in [Reference Bérard-BergeryBer82, Reference Koiso and SakaneKS86, Reference SakaneSak86, Reference Page and PopePP87, Reference Koiso and SakaneKS88, Reference Wang and WangWW98]. A common feature shared by positive Einstein metrics constructed in this series of works is that the principal orbits are principal ![]() $U(1)$ bundles over either a Fano manifold or a product of Fano manifolds. From this perspective, one can view the Einstein metric on
$U(1)$ bundles over either a Fano manifold or a product of Fano manifolds. From this perspective, one can view the Einstein metric on ![]() $\mathbb {HP}^{2}\sharp \overline {\mathbb {HP}}^{2}$ in [Reference BöhmBöh98] as another type of generalization to the Page metric, whose principal orbit is a principal
$\mathbb {HP}^{2}\sharp \overline {\mathbb {HP}}^{2}$ in [Reference BöhmBöh98] as another type of generalization to the Page metric, whose principal orbit is a principal ![]() $Sp(1)$ bundle over
$Sp(1)$ bundle over ![]() $\mathbb {HP}^1$.
$\mathbb {HP}^1$.
A natural question arises whether there exists a positive Einstein metric of cohomogeneity one on ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ with
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ with ![]() $m\geq 2$, where the principal orbit is the total space of the quaternionic Hopf fibration formed by the following group triple:
$m\geq 2$, where the principal orbit is the total space of the quaternionic Hopf fibration formed by the following group triple:
The condition of being ![]() $\mathsf {G}$-invariant reduces the Einstein equations to an ordinary differential equation (ODE) system defined on the one-dimensional orbit space. The solution takes the form
$\mathsf {G}$-invariant reduces the Einstein equations to an ordinary differential equation (ODE) system defined on the one-dimensional orbit space. The solution takes the form ![]() $g=dt^2+g(t),$ where
$g=dt^2+g(t),$ where ![]() $g(t)$ is a
$g(t)$ is a ![]() $\mathsf {G}$-invariant metric on
$\mathsf {G}$-invariant metric on ![]() $\mathbb {S}^{4m+3}$ for each
$\mathbb {S}^{4m+3}$ for each ![]() $t$. One looks for a
$t$. One looks for a ![]() $g(t)$ that is defined on a closed interval
$g(t)$ that is defined on a closed interval ![]() $[0, T]$ with an initial condition and a terminal condition. If
$[0, T]$ with an initial condition and a terminal condition. If ![]() $g(t)$ collapses to the quaternionic Kähler metric on the singular orbit
$g(t)$ collapses to the quaternionic Kähler metric on the singular orbit ![]() $\mathbb {HP}^m$ at
$\mathbb {HP}^m$ at ![]() $t=0$ and
$t=0$ and ![]() $t=T$, then
$t=T$, then ![]() $g$ defines a positive Einstein metric on the connected sum
$g$ defines a positive Einstein metric on the connected sum ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$, or equivalently, an
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$, or equivalently, an ![]() $\mathbb {S}^4$ bundle over
$\mathbb {S}^4$ bundle over ![]() $\mathbb {HP}^m$. It has been conjectured that such an Einstein metric exists on
$\mathbb {HP}^m$. It has been conjectured that such an Einstein metric exists on ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ for all
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ for all ![]() $m\geq 2$, as indicated by numerical evidence provided in [Reference Page and PopePP86, Reference BöhmBöh98, Reference Dancer, Hall and WangDHW13].
$m\geq 2$, as indicated by numerical evidence provided in [Reference Page and PopePP86, Reference BöhmBöh98, Reference Dancer, Hall and WangDHW13].
Some well-known Einstein metrics are realized as integral curves to the cohomogeneity-one Einstein equation. For example, the standard sphere metric, the sine cone over Jensen's sphere and the quaternionic Kähler metric on ![]() $\mathbb {HP}^{m+1}$ are represented by integral curves to the cohomogeneity-one system. Furthermore, the cone solution is an attractor to the system. It was realized in [Reference BöhmBöh98] that the winding of integral curves around the cone solution plays an important role in the existence problem described above. To investigate the winding, one studies a quantity (denoted by
$\mathbb {HP}^{m+1}$ are represented by integral curves to the cohomogeneity-one system. Furthermore, the cone solution is an attractor to the system. It was realized in [Reference BöhmBöh98] that the winding of integral curves around the cone solution plays an important role in the existence problem described above. To investigate the winding, one studies a quantity (denoted by ![]() $\sharp C_w(\bar {h})$ in [Reference BöhmBöh98]) that is assigned to each local solution that does not globally define a complete Einstein metric on
$\sharp C_w(\bar {h})$ in [Reference BöhmBöh98]) that is assigned to each local solution that does not globally define a complete Einstein metric on ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$. From the point of view of geometry, the quantity records the number of times that the principal orbit becomes isoparametric while its mean curvature remains positive. In general, an estimate for
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$. From the point of view of geometry, the quantity records the number of times that the principal orbit becomes isoparametric while its mean curvature remains positive. In general, an estimate for ![]() $\sharp C_w(\bar {h})$ can be obtained from the linearization along the cone solution. For
$\sharp C_w(\bar {h})$ can be obtained from the linearization along the cone solution. For ![]() $m=1$, the estimate is good enough to prove the global existence. This is not the case, however, if
$m=1$, the estimate is good enough to prove the global existence. This is not the case, however, if ![]() $m\geq 2$. For higher-dimensional cases, it is from the global analysis of the system that we obtain a further estimate for
$m\geq 2$. For higher-dimensional cases, it is from the global analysis of the system that we obtain a further estimate for ![]() $\sharp C_w(\bar {h})$ and we prove the following existence theorem.
$\sharp C_w(\bar {h})$ and we prove the following existence theorem.
Theorem 1.1 On each ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ with
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ with ![]() $m\geq 2$, there exists at least one positive Einstein metric with
$m\geq 2$, there exists at least one positive Einstein metric with ![]() $\mathsf {G}/\mathsf {K}=\mathbb {S}^{4m+3}$ as its principal orbit.
$\mathsf {G}/\mathsf {K}=\mathbb {S}^{4m+3}$ as its principal orbit.
Numerical studies in [Reference BöhmBöh98, Reference Dancer, Hall and WangDHW13] indicate that there exists another Einstein metric on ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ with
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ with ![]() $m\geq 2$. Based on Theorem 1.1, an estimate for
$m\geq 2$. Based on Theorem 1.1, an estimate for ![]() $\sharp C_w(\bar {h})$ in a limiting subsystem (essentially obtained from the linearization along the cone solution) helps us propose a criterion to check the existence of the second Einstein metric. Let
$\sharp C_w(\bar {h})$ in a limiting subsystem (essentially obtained from the linearization along the cone solution) helps us propose a criterion to check the existence of the second Einstein metric. Let ![]() $n$ be the dimension of
$n$ be the dimension of ![]() $\mathsf {G}/\mathsf {K}$. Such a criterion only depends on
$\mathsf {G}/\mathsf {K}$. Such a criterion only depends on ![]() $n$ (or
$n$ (or ![]() $m$).
$m$).
Theorem 1.2 Let ![]() $\theta _\Psi$ be the solution to the following initial value problem:
$\theta _\Psi$ be the solution to the following initial value problem:
 \begin{equation} \frac{d\theta}{d\eta}=\frac{n-1}{2n}\tanh\left(\frac{2\eta}{n}\right)\sin(2\theta)+ \frac{2}{n}\sqrt{\frac{(2m+1)(2m+2)(2m+3)}{(2m+3)^2+2m}},\quad \theta(0)=0. \end{equation}
\begin{equation} \frac{d\theta}{d\eta}=\frac{n-1}{2n}\tanh\left(\frac{2\eta}{n}\right)\sin(2\theta)+ \frac{2}{n}\sqrt{\frac{(2m+1)(2m+2)(2m+3)}{(2m+3)^2+2m}},\quad \theta(0)=0. \end{equation}
Let ![]() $\Omega =\lim _{\eta \to \infty }\theta _\Psi$. For
$\Omega =\lim _{\eta \to \infty }\theta _\Psi$. For ![]() $m\geq 2$, there exist at least two positive Einstein metrics on
$m\geq 2$, there exist at least two positive Einstein metrics on ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ if
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ if ![]() $\Omega < {3\pi }/{4}$.
$\Omega < {3\pi }/{4}$.
The upper bound for ![]() $\Omega$ in Theorem 1.2 is not sharp. Although it is difficult to solve the initial value problem (1.2) explicitly, one can use the Runge–Kutta fourth-order algorithm to approximate
$\Omega$ in Theorem 1.2 is not sharp. Although it is difficult to solve the initial value problem (1.2) explicitly, one can use the Runge–Kutta fourth-order algorithm to approximate ![]() $\Omega$. Since the right-hand side of (1.2) does not vanish at
$\Omega$. Since the right-hand side of (1.2) does not vanish at ![]() $\eta =0$, the initial Runge–Kutta step is well defined. Our numerical study shows that
$\eta =0$, the initial Runge–Kutta step is well defined. Our numerical study shows that ![]() $\Omega < {3\pi }/{4}$ for integers
$\Omega < {3\pi }/{4}$ for integers ![]() $m\in [2,100]$.
$m\in [2,100]$.
We also look into the case where ![]() $\mathsf {G}/\mathsf {K}$ completely collapses at two ends of a compact manifold. In that case, the cohomogeneity-one space is
$\mathsf {G}/\mathsf {K}$ completely collapses at two ends of a compact manifold. In that case, the cohomogeneity-one space is ![]() $\mathbb {S}^{4m+4}$. No new Einstein metric is found on
$\mathbb {S}^{4m+4}$. No new Einstein metric is found on ![]() $\mathbb {S}^{4m+4}$ for
$\mathbb {S}^{4m+4}$ for ![]() $m\geq 2$. For
$m\geq 2$. For ![]() $m=1$, however, we obtained a non-standard positive Einstein metric on
$m=1$, however, we obtained a non-standard positive Einstein metric on ![]() $\mathbb {S}^8$. Such a metric is inhomogeneous by the classification in [Reference ZillerZil82].
$\mathbb {S}^8$. Such a metric is inhomogeneous by the classification in [Reference ZillerZil82].
Theorem 1.3 There exists a non-standard ![]() $Sp(2)Sp(1)$-invariant positive Einstein metric
$Sp(2)Sp(1)$-invariant positive Einstein metric ![]() $\hat {g}_{\mathbb {S}^8}$ on
$\hat {g}_{\mathbb {S}^8}$ on ![]() $\mathbb {S}^{8}$.
$\mathbb {S}^{8}$.
It is worth mentioning that all new solutions found are symmetric. Metrics that are represented by these solutions all have a totally geodesic principal orbit.
This paper is structured as follows. In § 2 we present the dynamical system for positive Einstein metrics of cohomogeneity one with ![]() $\mathsf {G}/\mathsf {K}$ as the principal orbit. Then we apply a coordinate change that makes the cohomogeneity-one Ricci-flat system serve as a limiting subsystem. Initial conditions and terminal conditions are transformed into critical points of the new system. The new system admits
$\mathsf {G}/\mathsf {K}$ as the principal orbit. Then we apply a coordinate change that makes the cohomogeneity-one Ricci-flat system serve as a limiting subsystem. Initial conditions and terminal conditions are transformed into critical points of the new system. The new system admits ![]() $\mathbb {Z}_2$-symmetry. By a sign change, one can transform initial conditions into terminal conditions. Hence, the problem of finding globally defined positive Einstein metrics boils down to finding heteroclines that join two different critical points.
$\mathbb {Z}_2$-symmetry. By a sign change, one can transform initial conditions into terminal conditions. Hence, the problem of finding globally defined positive Einstein metrics boils down to finding heteroclines that join two different critical points.
In § 3 we compute linearizations of the critical points mentioned above and obtain two one-parameter families of locally defined positive Einstein metrics. One family is defined on a tubular neighborhood around ![]() $\mathbb {HP}^m$, represented by a one-parameter family of integral curves
$\mathbb {HP}^m$, represented by a one-parameter family of integral curves ![]() $\gamma _{s_1}$. The other family is defined on a neighborhood of a point in
$\gamma _{s_1}$. The other family is defined on a neighborhood of a point in ![]() $\mathbb {S}^{4m+4}$, represented by another one-parameter family of integral curves
$\mathbb {S}^{4m+4}$, represented by another one-parameter family of integral curves ![]() $\zeta _{s_2}$.
$\zeta _{s_2}$.
In § 4 we make a little modification to the quantity ![]() $\sharp C_w(\bar {h})$ in [Reference BöhmBöh98] and assign it to both
$\sharp C_w(\bar {h})$ in [Reference BöhmBöh98] and assign it to both ![]() $\gamma _{s_1}$ and
$\gamma _{s_1}$ and ![]() $\zeta _{s_2}$ (hence denoted by
$\zeta _{s_2}$ (hence denoted by ![]() $\sharp C(\gamma _{s_1})$ and
$\sharp C(\gamma _{s_1})$ and ![]() $\sharp C({\zeta _{s_2}})$). We construct a compact set to obtain an estimate for
$\sharp C({\zeta _{s_2}})$). We construct a compact set to obtain an estimate for ![]() $\sharp C(\gamma _{s_1})$ of some local solutions. Then we apply Lemma 4.4 in [Reference BöhmBöh98] and prove Theorem 1.1.
$\sharp C(\gamma _{s_1})$ of some local solutions. Then we apply Lemma 4.4 in [Reference BöhmBöh98] and prove Theorem 1.1.
In § 5 we apply another coordinate change that allows us to obtain more information on ![]() $\sharp C(\gamma _{s_1})$ and
$\sharp C(\gamma _{s_1})$ and ![]() $\sharp C(\zeta _{s_2})$, which is encoded in the initial value problem (1.2) in Theorem 1.2. We also prove Theorem 1.3.
$\sharp C(\zeta _{s_2})$, which is encoded in the initial value problem (1.2) in Theorem 1.2. We also prove Theorem 1.3.
Visual summaries of Theorem 1.1–1.3 are presented at the end of this paper.
2. Cohomogeneity-one system
Consider the group triple ![]() $(\mathsf {K},\mathsf {H},\mathsf {G})$ in (1.1). The isotropy representation
$(\mathsf {K},\mathsf {H},\mathsf {G})$ in (1.1). The isotropy representation ![]() $\mathfrak {g}/\mathfrak {k}$ consists of two inequivalent irreducible summands
$\mathfrak {g}/\mathfrak {k}$ consists of two inequivalent irreducible summands ![]() $\mathfrak {p}_1=\mathfrak {h}/\mathfrak {k}$ and
$\mathfrak {p}_1=\mathfrak {h}/\mathfrak {k}$ and ![]() $\mathfrak {p}_2=\mathfrak {g}/\mathfrak {h}$. Let the standard sphere metric
$\mathfrak {p}_2=\mathfrak {g}/\mathfrak {h}$. Let the standard sphere metric ![]() $g_{\mathbb {S}^{4m+3}}$ on
$g_{\mathbb {S}^{4m+3}}$ on ![]() $\mathsf {G}/\mathsf {K}=\mathbb {S}^{4m+3}$ be the background metric. As any
$\mathsf {G}/\mathsf {K}=\mathbb {S}^{4m+3}$ be the background metric. As any ![]() $\mathsf {G}$-invariant metric on
$\mathsf {G}$-invariant metric on ![]() $\mathsf {G}/\mathsf {K}$ is determined by its restriction to one tangent space
$\mathsf {G}/\mathsf {K}$ is determined by its restriction to one tangent space ![]() $\mathfrak {g}/\mathfrak {k}$, the metric takes the form
$\mathfrak {g}/\mathfrak {k}$, the metric takes the form
Let ![]() $f_1$ and
$f_1$ and ![]() $f_2$ be functions that are defined on the one-dimensional orbit space. We consider Einstein equations for the cohomogeneity-one metric
$f_2$ be functions that are defined on the one-dimensional orbit space. We consider Einstein equations for the cohomogeneity-one metric
By [Reference Eschenburg and WangEW00], the metric ![]() $g$ is an Einstein metric on
$g$ is an Einstein metric on ![]() $(t_*-\epsilon,t_*+\epsilon )\times \mathsf {G}/\mathsf {K}$ if
$(t_*-\epsilon,t_*+\epsilon )\times \mathsf {G}/\mathsf {K}$ if ![]() $(f_1,f_2)$ is a solution to
$(f_1,f_2)$ is a solution to
 \begin{equation} \begin{aligned} & \frac{\ddot{f_1}}{f_1}-\left(\frac{\dot{f_1}}{f_1}\right)^2=- \left(3 \frac{\dot{f_1}}{f_1}+4m\frac{\dot{f_2}}{f_2}\right) \frac{\dot{f_1}}{f_1}+2\frac{1}{f_1^2}+4m\frac{f_1^2}{f_2^4}-\Lambda,\\ & \frac{\ddot{f_2}}{f_2}-\left(\frac{\dot{f_2}}{f_2}\right)^2=- \left(3 \frac{\dot{f_1}}{f_1}+4m\frac{\dot{f_2}}{f_2}\right) \frac{\dot{f_2}}{f_2}+(4m+8)\frac{1}{f_2^2}-6\frac{f_1^2}{f_2^4}-\Lambda, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \frac{\ddot{f_1}}{f_1}-\left(\frac{\dot{f_1}}{f_1}\right)^2=- \left(3 \frac{\dot{f_1}}{f_1}+4m\frac{\dot{f_2}}{f_2}\right) \frac{\dot{f_1}}{f_1}+2\frac{1}{f_1^2}+4m\frac{f_1^2}{f_2^4}-\Lambda,\\ & \frac{\ddot{f_2}}{f_2}-\left(\frac{\dot{f_2}}{f_2}\right)^2=- \left(3 \frac{\dot{f_1}}{f_1}+4m\frac{\dot{f_2}}{f_2}\right) \frac{\dot{f_2}}{f_2}+(4m+8)\frac{1}{f_2^2}-6\frac{f_1^2}{f_2^4}-\Lambda, \end{aligned} \end{equation}with a conservation law
 \begin{equation} 3\left(\frac{\dot{f_1}}{f_1}\right)^2+4m \left(\frac{\dot{f_2}}{f_2}\right)^2-\left(d_1 \frac{\dot{f_1}}{f_1}+d_2 \frac{\dot{f_2}}{f_2}\right)^2+6\frac{1}{f_1^2}+4m(4m+8) \frac{1}{f_2^2}-12m\frac{f_1^2}{f_2^4}-(n-1)\Lambda=0. \end{equation}
\begin{equation} 3\left(\frac{\dot{f_1}}{f_1}\right)^2+4m \left(\frac{\dot{f_2}}{f_2}\right)^2-\left(d_1 \frac{\dot{f_1}}{f_1}+d_2 \frac{\dot{f_2}}{f_2}\right)^2+6\frac{1}{f_1^2}+4m(4m+8) \frac{1}{f_2^2}-12m\frac{f_1^2}{f_2^4}-(n-1)\Lambda=0. \end{equation}
To fix homothety, we set ![]() $\Lambda =n$ in this paper. We leave
$\Lambda =n$ in this paper. We leave ![]() $\Lambda$ in the equations for readers to trace the Einstein constant.
$\Lambda$ in the equations for readers to trace the Einstein constant.
Remark 2.1 If we replace the principal orbit ![]() $\mathsf {G}/\mathsf {K}$ by
$\mathsf {G}/\mathsf {K}$ by ![]() $\mathbb {S}^{4m+3}=[Sp(m+1)U(1)]/[Sp(m)\Delta U(1)]$, then the isotropy representation
$\mathbb {S}^{4m+3}=[Sp(m+1)U(1)]/[Sp(m)\Delta U(1)]$, then the isotropy representation ![]() $\mathfrak {g}/\mathfrak {k}$ consists of three inequivalent irreducible summands. The principal orbit can collapse either as
$\mathfrak {g}/\mathfrak {k}$ consists of three inequivalent irreducible summands. The principal orbit can collapse either as ![]() $\mathbb {HP}^m$ or
$\mathbb {HP}^m$ or ![]() $\mathbb {CP}^{2m+1}$, depending on the choice of intermediate group. For such a principal orbit, the dynamical system of cohomogeneity-one Einstein metrics involves three functions and has (2.1) as its subsystem. A numerical solution in [Reference Hiragane, Yasui and IshiharaHYI03] indicates the existence of a positive Einstein metric where
$\mathbb {CP}^{2m+1}$, depending on the choice of intermediate group. For such a principal orbit, the dynamical system of cohomogeneity-one Einstein metrics involves three functions and has (2.1) as its subsystem. A numerical solution in [Reference Hiragane, Yasui and IshiharaHYI03] indicates the existence of a positive Einstein metric where ![]() $\mathsf {G}/\mathsf {K}$ collapses to
$\mathsf {G}/\mathsf {K}$ collapses to ![]() $\mathbb {HP}^m$ at one end and
$\mathbb {HP}^m$ at one end and ![]() $\mathbb {CP}^{2m+1}$ at the other end.
$\mathbb {CP}^{2m+1}$ at the other end.
We consider (2.1) and (2.2) with the following two initial conditions. By [Reference Eschenburg and WangEW00], for the metric ![]() $g$ to extend smoothly to the singular orbit
$g$ to extend smoothly to the singular orbit ![]() $\mathbb {HP}^{m}$, we have
$\mathbb {HP}^{m}$, we have
for some ![]() $f>0$. On the other hand, for
$f>0$. On the other hand, for ![]() $g$ to extend smoothly to a point where
$g$ to extend smoothly to a point where ![]() $\mathsf {G}/\mathsf {K}$ fully collapses, one considers
$\mathsf {G}/\mathsf {K}$ fully collapses, one considers
By Myers’ theorem, any solution obtained from (2.1) that represents an Einstein metric on ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ must be defined on
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ must be defined on ![]() $[0,T]$ for some finite
$[0,T]$ for some finite ![]() $T>0$. Specifically, one looks for solutions with the initial condition (2.3) and the terminal condition
$T>0$. Specifically, one looks for solutions with the initial condition (2.3) and the terminal condition
for some ![]() $\bar {f}>0$. Similarly, to construct an Einstein metric on
$\bar {f}>0$. Similarly, to construct an Einstein metric on ![]() $\mathbb {S}^{4m+4}$, one looks for solutions with the initial condition (2.4) and the terminal condition
$\mathbb {S}^{4m+4}$, one looks for solutions with the initial condition (2.4) and the terminal condition
Remark 2.2 In [Reference KoisoKoi81], one takes a non-collapsed principal orbit ![]() $\mathsf {G}/\mathsf {K}$ as the initial data. Specifically, consider
$\mathsf {G}/\mathsf {K}$ as the initial data. Specifically, consider
for some positive ![]() $\bar {f}_i$. To construct a positive Einstein metric, one looks for a solution that extends backward and forward smoothly to either
$\bar {f}_i$. To construct a positive Einstein metric, one looks for a solution that extends backward and forward smoothly to either ![]() $\mathbb {HP}^m$ or a point on
$\mathbb {HP}^m$ or a point on ![]() $\mathbb {S}^{4m+4}$ in finite time.
$\mathbb {S}^{4m+4}$ in finite time.
Inspired by the coordinate change in [Reference Dancer and WangDW09] and a personal communication from Wei Yuan, we introduce a coordinate change that transforms (2.1) into a polynomial ODE system. Let ![]() $L$ be the shape operator of principal orbit. Define
$L$ be the shape operator of principal orbit. Define
 \[ X_1:=\frac{{\dot{f_1}}/{f_1}}{\sqrt{(\mathrm{tr}{L})^2+n\Lambda}},\quad X_2:=\frac{{\dot{f_2}}/{f_2}}{\sqrt{(\mathrm{tr}{L})^2+n\Lambda}},\quad Y:=\frac{{1}/{f_1}}{\sqrt{(\mathrm{tr}{L})^2+n\Lambda}},\quad Z:=\frac{{f_1}/{f_2^2}}{\sqrt{(\mathrm{tr}{L})^2+n\Lambda}}. \]
\[ X_1:=\frac{{\dot{f_1}}/{f_1}}{\sqrt{(\mathrm{tr}{L})^2+n\Lambda}},\quad X_2:=\frac{{\dot{f_2}}/{f_2}}{\sqrt{(\mathrm{tr}{L})^2+n\Lambda}},\quad Y:=\frac{{1}/{f_1}}{\sqrt{(\mathrm{tr}{L})^2+n\Lambda}},\quad Z:=\frac{{f_1}/{f_2^2}}{\sqrt{(\mathrm{tr}{L})^2+n\Lambda}}. \]
Also, define
 \begin{gather*} H:=3X_1+4mX_2,\quad G:=3X_1^2+4mX_2^2,\\ R_1:=2Y^2+4mZ^2,\quad R_2:=(4m+8)YZ-6Z^2. \end{gather*}
\begin{gather*} H:=3X_1+4mX_2,\quad G:=3X_1^2+4mX_2^2,\\ R_1:=2Y^2+4mZ^2,\quad R_2:=(4m+8)YZ-6Z^2. \end{gather*}
Consider ![]() $d\eta =\sqrt {\mathrm {tr}(L)^2+n\Lambda }dt$. Let
$d\eta =\sqrt {\mathrm {tr}(L)^2+n\Lambda }dt$. Let ![]() $'$ denote taking the derivative with respect to
$'$ denote taking the derivative with respect to ![]() $\eta$. Then (2.1) becomes
$\eta$. Then (2.1) becomes
 \begin{equation} \begin{bmatrix} X_1\\
X_2\\ Y\\ Z \end{bmatrix}'= V(X_1,X_2,Y,Z)= \begin{bmatrix}
X_1H\left(G+\dfrac{1}{n}
(1-H^2)-1\right)+R_1-\dfrac{1}{n}(1-H^2)\\
X_2H\left(G+\dfrac{1}{n} (1-H^2)-1\right)+R_2-\dfrac{1}{n}
(1-H^2)\\ Y\left(H\left(G+\dfrac{1}{n}
(1-H^2)\right)-X_1\right)\\ Z\left(H\left(G+\dfrac{1}{n}
(1-H^2)\right)+X_1-2X_2\right) \end{bmatrix}.
\end{equation}
\begin{equation} \begin{bmatrix} X_1\\
X_2\\ Y\\ Z \end{bmatrix}'= V(X_1,X_2,Y,Z)= \begin{bmatrix}
X_1H\left(G+\dfrac{1}{n}
(1-H^2)-1\right)+R_1-\dfrac{1}{n}(1-H^2)\\
X_2H\left(G+\dfrac{1}{n} (1-H^2)-1\right)+R_2-\dfrac{1}{n}
(1-H^2)\\ Y\left(H\left(G+\dfrac{1}{n}
(1-H^2)\right)-X_1\right)\\ Z\left(H\left(G+\dfrac{1}{n}
(1-H^2)\right)+X_1-2X_2\right) \end{bmatrix}.
\end{equation}
The conservation law (2.2) becomes
Or equivalently,
We can retrieve the original system by
 \begin{equation} t=\int_{\eta_*}^\eta \sqrt{\frac{1-H^2}{n\Lambda}} d\tilde{\eta},\quad f_1=\frac{1}{Y}\sqrt{\frac{1-H^2}{n\Lambda}},\quad f_2=\frac{1}{\sqrt{YZ}}\sqrt{\frac{1-H^2}{n\Lambda}}. \end{equation}
\begin{equation} t=\int_{\eta_*}^\eta \sqrt{\frac{1-H^2}{n\Lambda}} d\tilde{\eta},\quad f_1=\frac{1}{Y}\sqrt{\frac{1-H^2}{n\Lambda}},\quad f_2=\frac{1}{\sqrt{YZ}}\sqrt{\frac{1-H^2}{n\Lambda}}. \end{equation} It is clear that ![]() $H^2\leq 1$ by the definition of
$H^2\leq 1$ by the definition of ![]() $H$ and the
$H$ and the ![]() $X_i$. However, such a piece of information can be obtained from the new system alone without (2.1) and (2.2). Note that
$X_i$. However, such a piece of information can be obtained from the new system alone without (2.1) and (2.2). Note that
 \begin{align} H'&=\langle\nabla H, V\rangle \nonumber\\ &=H^2\left(G+\frac{1}{n}(1-H^2)-1\right)+6Y^2+4m(4m+8)YZ-12mZ^2-(1-H^2) \nonumber\\ &=H^2\left(G+\frac{1}{n}(1-H^2)-1\right)+1-G-\frac{1}{n}(1-H^2)-(1-H^2)\quad \text{by (2.8)} \nonumber\\ &=(H^2-1)\left(G+\frac{1}{n}(1-H^2)\right)=(H^2-1) \left(\frac{1}{n}+\frac{12m}{n}(X_1-X_2)^2\right). \end{align}
\begin{align} H'&=\langle\nabla H, V\rangle \nonumber\\ &=H^2\left(G+\frac{1}{n}(1-H^2)-1\right)+6Y^2+4m(4m+8)YZ-12mZ^2-(1-H^2) \nonumber\\ &=H^2\left(G+\frac{1}{n}(1-H^2)-1\right)+1-G-\frac{1}{n}(1-H^2)-(1-H^2)\quad \text{by (2.8)} \nonumber\\ &=(H^2-1)\left(G+\frac{1}{n}(1-H^2)\right)=(H^2-1) \left(\frac{1}{n}+\frac{12m}{n}(X_1-X_2)^2\right). \end{align}
Therefore, the algebraic surface in ![]() $\mathbb {R}^4$ with boundary
$\mathbb {R}^4$ with boundary
is invariant. Moreover, ![]() $\mathcal {E}\cap \{H=\pm 1\}$ are two invariant sets of lower dimension. The
$\mathcal {E}\cap \{H=\pm 1\}$ are two invariant sets of lower dimension. The ![]() $\mathbb {Z}_2$-symmetry on the sign of
$\mathbb {Z}_2$-symmetry on the sign of ![]() $(X_1,X_2)$ gives a one-to-one correspondence between integral curves on
$(X_1,X_2)$ gives a one-to-one correspondence between integral curves on ![]() $\mathcal {E}\cap \{H= 1\}$ and those on
$\mathcal {E}\cap \{H= 1\}$ and those on ![]() $\mathcal {E}\cap \{H= -1\}$.
$\mathcal {E}\cap \{H= -1\}$.
Remark 2.3 The restricted system of (2.7) on ![]() $\mathcal {E}\cap \{H= 1\}$ is in fact (2.1) with
$\mathcal {E}\cap \{H= 1\}$ is in fact (2.1) with ![]() $\Lambda =0$ under the coordinate change
$\Lambda =0$ under the coordinate change ![]() $d\eta =(\mathrm {tr}{L}) dt$. The dynamical system is essentially the same as the one that appears in [Reference WinkWin17]. An integral curve on the subsystem is known for representing a complete Ricci-flat metric defined on the non-compact manifold
$d\eta =(\mathrm {tr}{L}) dt$. The dynamical system is essentially the same as the one that appears in [Reference WinkWin17]. An integral curve on the subsystem is known for representing a complete Ricci-flat metric defined on the non-compact manifold ![]() $\mathbb {HP}^{m+1}\backslash \{*\}$ [Reference BöhmBöh98]. The Ricci-flat metric on
$\mathbb {HP}^{m+1}\backslash \{*\}$ [Reference BöhmBöh98]. The Ricci-flat metric on ![]() $\mathbb {HP}^{m+1}\backslash \{*\}$ is the limit cone for locally defined positive Einstein metrics on the tubular neighborhood around
$\mathbb {HP}^{m+1}\backslash \{*\}$ is the limit cone for locally defined positive Einstein metrics on the tubular neighborhood around ![]() $\mathbb {HP}^m$.
$\mathbb {HP}^m$.
Remark 2.4 If an integral curve to (2.7) enters ![]() $\mathcal {E}\cap \{H<1\}$ and is defined on
$\mathcal {E}\cap \{H<1\}$ and is defined on ![]() $\mathbb {R}$, then from (2.11) it must cross
$\mathbb {R}$, then from (2.11) it must cross ![]() $\mathcal {E}\cap \{H=0\}$ transversally. The crossing point corresponds to the turning point in [Reference BöhmBöh98]. For any integral curve to (2.7) that has a turning point, we choose the
$\mathcal {E}\cap \{H=0\}$ transversally. The crossing point corresponds to the turning point in [Reference BöhmBöh98]. For any integral curve to (2.7) that has a turning point, we choose the ![]() $\eta _*$ in (2.10) so that
$\eta _*$ in (2.10) so that ![]() $t_*:= \int _{\eta _*}^0 \sqrt { ({1-H^2})/{n\Lambda }}\, d\tilde {\eta }$ is the value at which
$t_*:= \int _{\eta _*}^0 \sqrt { ({1-H^2})/{n\Lambda }}\, d\tilde {\eta }$ is the value at which ![]() $\mathrm {tr}{L}$ vanishes. By our choice of
$\mathrm {tr}{L}$ vanishes. By our choice of ![]() $\eta _*$, the integral curve crosses
$\eta _*$, the integral curve crosses ![]() $\mathcal {E}\cap \{H=0\}$ at
$\mathcal {E}\cap \{H=0\}$ at ![]() $\eta =0$. There are cohomogeneity-one Einstein systems with additional geometric structure, such as the one considered in [Reference Foscolo and HaskinsFH17], where every trajectory has a turning point.
$\eta =0$. There are cohomogeneity-one Einstein systems with additional geometric structure, such as the one considered in [Reference Foscolo and HaskinsFH17], where every trajectory has a turning point.
Remark 2.5 From (2.9), the inequality ![]() $6Y^2+4m(4m+8)YZ-12mZ^2\leq 1- {1}/{n}$ is always valid. Therefore, the set
$6Y^2+4m(4m+8)YZ-12mZ^2\leq 1- {1}/{n}$ is always valid. Therefore, the set ![]() $\mathcal {E}\cap \{Z-\rho Y\leq 0\}$ is compact for any fixed
$\mathcal {E}\cap \{Z-\rho Y\leq 0\}$ is compact for any fixed ![]() $\rho \in [0, ({m(4m+8)+\sqrt {m^2(4m+8)^2+18m}})/{6m})$. If the maximal interval of existence of an integral curve to (2.7) is
$\rho \in [0, ({m(4m+8)+\sqrt {m^2(4m+8)^2+18m}})/{6m})$. If the maximal interval of existence of an integral curve to (2.7) is ![]() $(-\infty,\bar {\eta })$ for some
$(-\infty,\bar {\eta })$ for some ![]() $\bar {\eta }\in \mathbb {R}$, it must escape
$\bar {\eta }\in \mathbb {R}$, it must escape ![]() $\mathcal {E}\cap \{Z-\rho Y\leq 0\}$. The crossing point corresponds to the W-intersection point in [Reference BöhmBöh98]. In Proposition 3.3 and Definition 4.9, we introduce an invariant set
$\mathcal {E}\cap \{Z-\rho Y\leq 0\}$. The crossing point corresponds to the W-intersection point in [Reference BöhmBöh98]. In Proposition 3.3 and Definition 4.9, we introduce an invariant set ![]() $\mathcal {W}$ and a modified definition for the
$\mathcal {W}$ and a modified definition for the ![]() $W$-intersection point, which fixes
$W$-intersection point, which fixes ![]() $\rho =1$ in the original definition in [Reference BöhmBöh98].
$\rho =1$ in the original definition in [Reference BöhmBöh98].
3. Linearization at critical points
The local existence of positive Einstein metrics around the singular orbit ![]() $\mathbb {HP}^{m}$ is well established in [Reference BöhmBöh98]. We interpret the result using the new coordinate. For
$\mathbb {HP}^{m}$ is well established in [Reference BöhmBöh98]. We interpret the result using the new coordinate. For ![]() $m\geq 2$, the vector field
$m\geq 2$, the vector field ![]() $V$ has in total
$V$ has in total ![]() $10$ critical points (
$10$ critical points (![]() $12$ critical points for
$12$ critical points for ![]() $m=1$) on
$m=1$) on ![]() $\mathcal {E}$. As indicated by their superscripts, these critical points lie on either
$\mathcal {E}$. As indicated by their superscripts, these critical points lie on either ![]() $\mathcal {E}\cap \{H=1\}$ or
$\mathcal {E}\cap \{H=1\}$ or ![]() $\mathcal {E}\cap \{H=-1\}$.
$\mathcal {E}\cap \{H=-1\}$.
–
 $p_0^\pm =\big(\!\pm \frac {1}{3},0,\frac {1}{3},0\big )$
$p_0^\pm =\big(\!\pm \frac {1}{3},0,\frac {1}{3},0\big )$These points represent the initial condition (2.3) and the terminal condition (2.5). Integral curves that emanate from
 $p_0^+$ and enter
$p_0^+$ and enter  $\mathcal {E}\cap \{H<1\}$ represent positive Einstein metrics defined on a tubular neighborhood around
$\mathcal {E}\cap \{H<1\}$ represent positive Einstein metrics defined on a tubular neighborhood around  $\mathbb {HP}^m$. A complete Einstein metric on
$\mathbb {HP}^m$. A complete Einstein metric on  $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ is represented by a heterocline that joins
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ is represented by a heterocline that joins  $p_0^\pm$.
$p_0^\pm$.–
 $p_1^\pm =(\pm ({1}/{n}),\pm ({1}/{n}), {1}/{n}, {1}/{n})$
$p_1^\pm =(\pm ({1}/{n}),\pm ({1}/{n}), {1}/{n}, {1}/{n})$These points represent the initial condition (2.4) and the terminal condition (2.6). Integral curves that emanate from
 $p_0^+$ and enter
$p_0^+$ and enter  $\mathcal {E}\cap \{H<1\}$ represent positive Einstein metrics defined on a tubular neighborhood around a point on
$\mathcal {E}\cap \{H<1\}$ represent positive Einstein metrics defined on a tubular neighborhood around a point on  $\mathbb {S}^{4m+4}$. The standard sphere metric is represented by a straight line that joins
$\mathbb {S}^{4m+4}$. The standard sphere metric is represented by a straight line that joins  $p_1^\pm$. It is also worth mentioning that the quaternionic Kähler metric on
$p_1^\pm$. It is also worth mentioning that the quaternionic Kähler metric on  $\mathbb {HP}^{m+1}$ (respectively,
$\mathbb {HP}^{m+1}$ (respectively,  $\overline {\mathbb {HP}}^{m+1}$) is represented by an integral curve that joins
$\overline {\mathbb {HP}}^{m+1}$) is represented by an integral curve that joins  $p_0^+$ and
$p_0^+$ and  $p_1^-$ (respectively,
$p_1^-$ (respectively,  $p_0^-$ and
$p_0^-$ and  $p_1^+$).
$p_1^+$).–
 $p_2^\pm =(\pm ({1}/{n}),\pm ({1}/{n}),(2m+3)z_0,z_0), z_0= ({1}/{n})\sqrt { ({2m+1})/({2m+(2m+3)^2})}$
$p_2^\pm =(\pm ({1}/{n}),\pm ({1}/{n}),(2m+3)z_0,z_0), z_0= ({1}/{n})\sqrt { ({2m+1})/({2m+(2m+3)^2})}$These points represent the initial condition and the terminal condition where the principal orbit collapses as Jensen's sphere [Reference JensenJen73]. There is only one integral curve that emanates from
 $p_2^+$ and it represents the singular sine metric cone with its base as Jensen's sphere [Reference JensenJen73]. It is also worth mentioning that
$p_2^+$ and it represents the singular sine metric cone with its base as Jensen's sphere [Reference JensenJen73]. It is also worth mentioning that  $p_2^+$ is a sink for the Ricci-flat subsystem of (2.7) restricted on
$p_2^+$ is a sink for the Ricci-flat subsystem of (2.7) restricted on  $\mathcal {E}\cap \{H=1\}$, representing the asymptotically conical limit.
$\mathcal {E}\cap \{H=1\}$, representing the asymptotically conical limit.–
 $q_1^\pm =(\pm (({3+ 2\sqrt {12m^2+6m}})/{3n}),\pm (({4m-2\sqrt {12m^2+6m}})/{4mn}),0,0),$
$q_1^\pm =(\pm (({3+ 2\sqrt {12m^2+6m}})/{3n}),\pm (({4m-2\sqrt {12m^2+6m}})/{4mn}),0,0),$
 $q_2^\pm =(\pm (({3-2 \sqrt {12m^2+6m}})/{3n}),\pm (({4m+2\sqrt {12m^2+6m}})/{4mn}),0,0)$
$q_2^\pm =(\pm (({3-2 \sqrt {12m^2+6m}})/{3n}),\pm (({4m+2\sqrt {12m^2+6m}})/{4mn}),0,0)$These critical points are in general ‘bad’ points for our study. Integral curves that converge to
 $q_1^-$ or
$q_1^-$ or  $q_2^-$ represent metrics with blown-up
$q_2^-$ represent metrics with blown-up  $\dot {f}_1$ and
$\dot {f}_1$ and  $\dot {f}_2$. Straightforward computations show that for
$\dot {f}_2$. Straightforward computations show that for  $m\geq 2$, critical points
$m\geq 2$, critical points  $q_1^+$ and
$q_1^+$ and  $q_2^+$ are sources for (2.7) on (2.8). By the
$q_2^+$ are sources for (2.7) on (2.8). By the  $\mathbb {Z}_2$ symmetry, critical points
$\mathbb {Z}_2$ symmetry, critical points  $q_1^-$ and
$q_1^-$ and  $q_2^-$ are sinks for
$q_2^-$ are sinks for  $m\geq 2$.
$m\geq 2$.–
 $q_3^\pm =(\mp \frac {1}{3},\pm ({2}/{4m}),0, {\sqrt {3-2m}}/{6m})$
$q_3^\pm =(\mp \frac {1}{3},\pm ({2}/{4m}),0, {\sqrt {3-2m}}/{6m})$These critical points are also ‘bad’ points as
 $q_1^\pm$ and
$q_1^\pm$ and  $q_2^\pm$. They only exist for
$q_2^\pm$. They only exist for  $m=1$. Integral curves that converge to
$m=1$. Integral curves that converge to  $q_3^-$ represent metrics with blown-up
$q_3^-$ represent metrics with blown-up  $\dot {f_1}$. For
$\dot {f_1}$. For  $m=1$, critical points
$m=1$, critical points  $q_1^+$ and
$q_1^+$ and  $q_3^+$ are sources and
$q_3^+$ are sources and  $q_1^-$ and
$q_1^-$ and  $q_3^-$ are sinks;
$q_3^-$ are sinks;  $q_2^+$ and
$q_2^+$ and  $q_2^-$ are saddles.
$q_2^-$ are saddles.
Proposition 3.1 The list above exhausts all critical points on ![]() $\mathcal {E}$.
$\mathcal {E}$.
Proof. By (2.11), it is clear that critical points on ![]() $\mathcal {E}$ must lie on
$\mathcal {E}$ must lie on ![]() $\{H^2=1\}$. The list is complete by considering the vanishing of the
$\{H^2=1\}$. The list is complete by considering the vanishing of the ![]() $Y$-entry and
$Y$-entry and ![]() $Z$-entry.
$Z$-entry.
For any ![]() $m$, linearizations at
$m$, linearizations at ![]() $q_i^\pm$ show that the phase space
$q_i^\pm$ show that the phase space ![]() $\mathcal {E}$ is ‘filled’ with integral curves that emanate from
$\mathcal {E}$ is ‘filled’ with integral curves that emanate from ![]() $q_i^+$ or those that converge to
$q_i^+$ or those that converge to ![]() $q_i^-$. Hence, most integral curves that emanate from
$q_i^-$. Hence, most integral curves that emanate from ![]() $p_0^+$ or
$p_0^+$ or ![]() $p_1^+$ are anticipated to converge to one of these
$p_1^+$ are anticipated to converge to one of these ![]() $q_i^-$. In the following, we give a detailed analysis of the linearizations at
$q_i^-$. In the following, we give a detailed analysis of the linearizations at ![]() $p_0^+$ and
$p_0^+$ and ![]() $p_1^+$ and integral curves that emanate from these critical points.
$p_1^+$ and integral curves that emanate from these critical points.
The linearization at ![]() $p_0^+$ is
$p_0^+$ is
 \[ \begin{bmatrix} -\dfrac{8m-6}{3n} &
-\dfrac{32m^2-24m}{9n} & \dfrac{4}{3} & 0\\ \dfrac{6}{n} &
\dfrac{16m-6}{3n} & 0 & \dfrac{4m+8}{3}\\ \dfrac{8m}{3n} &
\dfrac{16m^2-12m}{9n} & 0 & 0\\ 0 & 0 & 0 & \dfrac{2}{3}
\end{bmatrix}. \]
\[ \begin{bmatrix} -\dfrac{8m-6}{3n} &
-\dfrac{32m^2-24m}{9n} & \dfrac{4}{3} & 0\\ \dfrac{6}{n} &
\dfrac{16m-6}{3n} & 0 & \dfrac{4m+8}{3}\\ \dfrac{8m}{3n} &
\dfrac{16m^2-12m}{9n} & 0 & 0\\ 0 & 0 & 0 & \dfrac{2}{3}
\end{bmatrix}. \]
Eigenvalues and eigenvectors are
 \begin{gather*} \lambda_1=\lambda_2=\frac{2}{3},\quad \lambda_3=-\frac{2}{3},\quad \lambda_4=\frac{8m}{3n};\\ v_1=\begin{bmatrix} -(8m^2+18m+18)\\ -9\\ -(8m^2+18m)\\ 9 \end{bmatrix},\quad v_2=\begin{bmatrix} -4m(m+2)\\ 3(m+2)\\ -2m(m+2)\\ 3 \end{bmatrix},\quad v_3=\begin{bmatrix} -4m\\ 3\\ 2m\\ 0 \end{bmatrix},\quad v_4=\begin{bmatrix} -2(4m-3)\\ 18\\ 4m-3\\ 0 \end{bmatrix}. \end{gather*}
\begin{gather*} \lambda_1=\lambda_2=\frac{2}{3},\quad \lambda_3=-\frac{2}{3},\quad \lambda_4=\frac{8m}{3n};\\ v_1=\begin{bmatrix} -(8m^2+18m+18)\\ -9\\ -(8m^2+18m)\\ 9 \end{bmatrix},\quad v_2=\begin{bmatrix} -4m(m+2)\\ 3(m+2)\\ -2m(m+2)\\ 3 \end{bmatrix},\quad v_3=\begin{bmatrix} -4m\\ 3\\ 2m\\ 0 \end{bmatrix},\quad v_4=\begin{bmatrix} -2(4m-3)\\ 18\\ 4m-3\\ 0 \end{bmatrix}. \end{gather*}
The first three eigenvectors are tangent to ![]() $\mathcal {E}$. Consider linearized solutions of the form
$\mathcal {E}$. Consider linearized solutions of the form
for some ![]() $s_1\in \mathbb {R}$. By the Hartman–Grobman theorem, there is a one-to-one correspondence between each choice of
$s_1\in \mathbb {R}$. By the Hartman–Grobman theorem, there is a one-to-one correspondence between each choice of ![]() $s_1\in \mathbb {R}$ and an actual solution curve that emanates from
$s_1\in \mathbb {R}$ and an actual solution curve that emanates from ![]() $p_0^+$ and leaves
$p_0^+$ and leaves ![]() $\mathcal {E}\cap \{H=1\}$ initially. Hence, we use
$\mathcal {E}\cap \{H=1\}$ initially. Hence, we use ![]() $\gamma _{s_1}$ to denote an actual solution that approaches the linearized solution (3.1) near
$\gamma _{s_1}$ to denote an actual solution that approaches the linearized solution (3.1) near ![]() $p_0^+$. Moreover, by the unstable version of Theorem 4.5 in Chapter 13 of [Reference Coddington and LevinsonCL55], there is some
$p_0^+$. Moreover, by the unstable version of Theorem 4.5 in Chapter 13 of [Reference Coddington and LevinsonCL55], there is some ![]() $\epsilon >0$ such that
$\epsilon >0$ such that
From the linearization at ![]() $p_0^+$ and (2.10), the parameter
$p_0^+$ and (2.10), the parameter ![]() $s_1$ is related to the initial condition
$s_1$ is related to the initial condition ![]() $f$ in (2.3) as follows.
$f$ in (2.3) as follows.
We set ![]() $s_1>-3$ so that
$s_1>-3$ so that ![]() $f$ is positive. From another perspective, in order to have
$f$ is positive. From another perspective, in order to have ![]() $\gamma _{s_1}$ be in
$\gamma _{s_1}$ be in ![]() $\mathcal {E}$, we only consider
$\mathcal {E}$, we only consider ![]() $\gamma _{s_1}$ with
$\gamma _{s_1}$ with ![]() $s_1> -3$ so that
$s_1> -3$ so that ![]() $Z$ is positive initially along the integral curve. Note that
$Z$ is positive initially along the integral curve. Note that ![]() $v_2$ is tangent to
$v_2$ is tangent to ![]() $\mathcal {E}\cap \{H=1\}$. Therefore, it makes sense to let
$\mathcal {E}\cap \{H=1\}$. Therefore, it makes sense to let ![]() $\gamma _\infty$ denote the integral curve that lies in
$\gamma _\infty$ denote the integral curve that lies in ![]() $\mathcal {E}\cap \{H=1\}$ such that
$\mathcal {E}\cap \{H=1\}$ such that
near ![]() $p_0^+$. The integral curve
$p_0^+$. The integral curve ![]() $\gamma _\infty$ represents the Ricci-flat metric on
$\gamma _\infty$ represents the Ricci-flat metric on ![]() $\mathbb {HP}^{m+1}\backslash \{*\}$ constructed in [Reference BöhmBöh98]. For
$\mathbb {HP}^{m+1}\backslash \{*\}$ constructed in [Reference BöhmBöh98]. For ![]() $m=1$, the metric is the
$m=1$, the metric is the ![]() $\mathrm {Spin}(7)$ metric in [Reference Bryant and SalamonBS89] and [Reference Gibbons, Page and PopeGPP90]. Furthermore, as shown in Proposition 6.3 in [Reference ChiChi21], the integral curve
$\mathrm {Spin}(7)$ metric in [Reference Bryant and SalamonBS89] and [Reference Gibbons, Page and PopeGPP90]. Furthermore, as shown in Proposition 6.3 in [Reference ChiChi21], the integral curve ![]() $\gamma _\infty$ lies on the one-dimensional invariant set
$\gamma _\infty$ lies on the one-dimensional invariant set
and joins ![]() $p_0^+$ and
$p_0^+$ and ![]() $p_2^+$.
$p_2^+$.
Remark 3.2 The defining equations in (3.4) are equivalent to the cohomogeneity-one ![]() $\mathrm {Spin}(7)$ condition on
$\mathrm {Spin}(7)$ condition on ![]() $\mathbb {HP}^2\backslash \{*\}$. Specifically, we have the dynamical system
$\mathbb {HP}^2\backslash \{*\}$. Specifically, we have the dynamical system
 \begin{equation} \begin{aligned} & \frac{\dot{f_1}}{f_1}=\frac{1}{f_1}-2\frac{f_1}{f_2^2},\\ & \frac{\dot{f_2}}{f_2}=3\frac{f_1}{f_2^2}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \frac{\dot{f_1}}{f_1}=\frac{1}{f_1}-2\frac{f_1}{f_2^2},\\ & \frac{\dot{f_2}}{f_2}=3\frac{f_1}{f_2^2}. \end{aligned} \end{equation}
Similar to the initial value problem in Remark 3.6, the initial condition can be obtained from the coordinate of ![]() $p_0^+$ and the limit
$p_0^+$ and the limit ![]() $\lim _{\eta \to -\infty }( {X_2}/{\sqrt {YZ}})(\gamma _\infty (\eta ))$. Since a Ricci-flat metric is homothety invariant, the extra freedom allows us to set
$\lim _{\eta \to -\infty }( {X_2}/{\sqrt {YZ}})(\gamma _\infty (\eta ))$. Since a Ricci-flat metric is homothety invariant, the extra freedom allows us to set ![]() $f_2(0)$ as any positive number. Solving the initial value problem with
$f_2(0)$ as any positive number. Solving the initial value problem with
yields the homothetic family of ![]() $\mathrm {Spin}(7)$ metrics in [Reference Bryant and SalamonBS89] and [Reference Gibbons, Page and PopeGPP90].
$\mathrm {Spin}(7)$ metrics in [Reference Bryant and SalamonBS89] and [Reference Gibbons, Page and PopeGPP90].
The linearization at ![]() $p_1^+$ is
$p_1^+$ is
 \[ \begin{bmatrix}
-\dfrac{16m^2+8m-6}{n^2} & \dfrac{16m(m+1)}{n^2} &
\dfrac{4}{n} & \dfrac{8m}{n}\\ \dfrac{12m+12}{n^2} &
-\dfrac{4m+6}{n^2} & \dfrac{4m+8}{n} & \dfrac{4m-4}{n}\\
-\dfrac{4m}{n^2} & \dfrac{4m}{n^2} & 0 & 0\\
\dfrac{4m+6}{n^2} & -\dfrac{4m+6}{n^2} & 0 & 0
\end{bmatrix}. \]
\[ \begin{bmatrix}
-\dfrac{16m^2+8m-6}{n^2} & \dfrac{16m(m+1)}{n^2} &
\dfrac{4}{n} & \dfrac{8m}{n}\\ \dfrac{12m+12}{n^2} &
-\dfrac{4m+6}{n^2} & \dfrac{4m+8}{n} & \dfrac{4m-4}{n}\\
-\dfrac{4m}{n^2} & \dfrac{4m}{n^2} & 0 & 0\\
\dfrac{4m+6}{n^2} & -\dfrac{4m+6}{n^2} & 0 & 0
\end{bmatrix}. \]
Eigenvalues and eigenvectors are
 \begin{gather*} \mu_1=\mu_2=\frac{2}{n},\quad \mu_3=0,\quad \mu_4=-\frac{4(m+1)}{n};\\ w_1=\begin{bmatrix} -1\\ -1\\ 0\\ 0 \end{bmatrix},\quad w_2=\begin{bmatrix} -4m\\ 3\\ 2m\\ -(2m+3) \end{bmatrix},\quad w_3=\begin{bmatrix} -(n-1)\\ -(n-1)\\ 1\\ 1 \end{bmatrix},\quad w_4=\begin{bmatrix} -8m(m+1)\\ 6(m+1)\\ -2m\\ 2m+3 \end{bmatrix}. \end{gather*}
\begin{gather*} \mu_1=\mu_2=\frac{2}{n},\quad \mu_3=0,\quad \mu_4=-\frac{4(m+1)}{n};\\ w_1=\begin{bmatrix} -1\\ -1\\ 0\\ 0 \end{bmatrix},\quad w_2=\begin{bmatrix} -4m\\ 3\\ 2m\\ -(2m+3) \end{bmatrix},\quad w_3=\begin{bmatrix} -(n-1)\\ -(n-1)\\ 1\\ 1 \end{bmatrix},\quad w_4=\begin{bmatrix} -8m(m+1)\\ 6(m+1)\\ -2m\\ 2m+3 \end{bmatrix}. \end{gather*}
The first three eigenvectors are tangent to ![]() $\mathcal {E}$. Hence, there exists a one-parameter family of integral curves
$\mathcal {E}$. Hence, there exists a one-parameter family of integral curves ![]() $\zeta _{s_2}$ that emanate from
$\zeta _{s_2}$ that emanate from ![]() $p_1^+$ and
$p_1^+$ and
The initial condition (2.4) has a degree of freedom in the second-order derivative. Specifically, the parameter ![]() $s_2$ is related to the limit
$s_2$ is related to the limit ![]() $\lim _{t\to 0} ({\ddot {f_2}}/{f_2}) ({f_1}/{\ddot {f_1}})$. From (2.1), (2.10) and the linearization at
$\lim _{t\to 0} ({\ddot {f_2}}/{f_2}) ({f_1}/{\ddot {f_1}})$. From (2.1), (2.10) and the linearization at ![]() $p_1^+$, we have
$p_1^+$, we have
 \begin{equation} \lim_{t\to 0}\frac{\ddot{f_2}}{f_2}\frac{f_1}{\ddot{f_1}}= \lim_{\eta\to -\infty}\frac{X_2^2-HX_2+R_2-\frac{1-H^2}{n}}{X_1^2-HX_1+R_1-\frac{1-H^2}{n}}= \frac{n}{4m(1+6ms_2)}-\frac{9}{12m}. \end{equation}
\begin{equation} \lim_{t\to 0}\frac{\ddot{f_2}}{f_2}\frac{f_1}{\ddot{f_1}}= \lim_{\eta\to -\infty}\frac{X_2^2-HX_2+R_2-\frac{1-H^2}{n}}{X_1^2-HX_1+R_1-\frac{1-H^2}{n}}= \frac{n}{4m(1+6ms_2)}-\frac{9}{12m}. \end{equation}
Although it is clear that ![]() $\zeta _{s_2}$ is in
$\zeta _{s_2}$ is in ![]() $\mathcal {E}$ for any
$\mathcal {E}$ for any ![]() $s_2\in \mathbb {R}$, we mainly consider
$s_2\in \mathbb {R}$, we mainly consider ![]() $s_2\geq 0$ in this paper. We have the following proposition for
$s_2\geq 0$ in this paper. We have the following proposition for ![]() $\zeta _{s_2}$ with
$\zeta _{s_2}$ with ![]() $s_2<0$.
$s_2<0$.
Proposition 3.3 Each ![]() $\zeta _{s_2}$ with
$\zeta _{s_2}$ with ![]() $s_2<0$ either does not converge to any critical point in
$s_2<0$ either does not converge to any critical point in ![]() $\mathcal {E}$ or converges to
$\mathcal {E}$ or converges to ![]() $q_2^-$ (
$q_2^-$ (![]() $q_2^-$ or
$q_2^-$ or ![]() $q_3^-$ if
$q_3^-$ if ![]() $m=1$).
$m=1$).
Proof. From the linearized solution, it is clear that each ![]() $\zeta _{s_2}$ with
$\zeta _{s_2}$ with ![]() $s_2<0$ is initially in
$s_2<0$ is initially in
As ![]() $\mathcal {W}$ includes all points
$\mathcal {W}$ includes all points ![]() $(\sqrt { ({n-1})/{12m}}\cosh (\lambda ),0,0,\sqrt { ({n-1})/{12nm}}\sinh (\lambda ))$ with
$(\sqrt { ({n-1})/{12m}}\cosh (\lambda ),0,0,\sqrt { ({n-1})/{12nm}}\sinh (\lambda ))$ with ![]() $\lambda \geq 0$, the set is non-compact. Furthermore, since
$\lambda \geq 0$, the set is non-compact. Furthermore, since
and
the set ![]() $\mathcal {W}$ is invariant. Note that the second term in (3.10) is non-negative in
$\mathcal {W}$ is invariant. Note that the second term in (3.10) is non-negative in ![]() $\mathcal {W}\cap \{X_1-X_2=0\}$.
$\mathcal {W}\cap \{X_1-X_2=0\}$.
By (3.9), it is clear that the function ![]() $ {Y}/{Z}$ monotonically decreases from
$ {Y}/{Z}$ monotonically decreases from ![]() $1$ along each
$1$ along each ![]() $\zeta _{s_2}$ with
$\zeta _{s_2}$ with ![]() $s_2<0$. If the function
$s_2<0$. If the function ![]() $ {Y}/{Z}$ converges to some positive number, the function
$ {Y}/{Z}$ converges to some positive number, the function ![]() $X_1-X_2$ would converge to zero. From (2.9), we know that both
$X_1-X_2$ would converge to zero. From (2.9), we know that both ![]() $Y$ and
$Y$ and ![]() $Z$ converge to some positive numbers with
$Z$ converge to some positive numbers with ![]() $ {Y}/{Z}<1$. Hence, the right-hand side of (3.10) is eventually positive as
$ {Y}/{Z}<1$. Hence, the right-hand side of (3.10) is eventually positive as ![]() $X_1-X_2$ converges to zero, a contradiction. Hence, the function
$X_1-X_2$ converges to zero, a contradiction. Hence, the function ![]() $ {Y}/{Z}$ converges to zero. Therefore, if a
$ {Y}/{Z}$ converges to zero. Therefore, if a ![]() $\zeta _{s_2}$ with
$\zeta _{s_2}$ with ![]() $s_2<0$ converges to a critical point in
$s_2<0$ converges to a critical point in ![]() $\mathcal {E}$, it must be
$\mathcal {E}$, it must be ![]() $q_2^-$ (
$q_2^-$ (![]() $q_2^-$ or
$q_2^-$ or ![]() $q_3^-$ if
$q_3^-$ if ![]() $m=1$).
$m=1$).
Remark 3.4 For ![]() $s_2=0$, it is clear that
$s_2=0$, it is clear that ![]() $\zeta _0$ lies on the one-dimensional invariant set
$\zeta _0$ lies on the one-dimensional invariant set
and joins ![]() $p_1^\pm$. The integral curve represents the standard sphere metric
$p_1^\pm$. The integral curve represents the standard sphere metric ![]() $g_{\mathbb {S}^{4m+4}}$ on
$g_{\mathbb {S}^{4m+4}}$ on ![]() $\mathbb {S}^{4m+4}$. Specifically, the defining equations in (3.11) give the initial value problem
$\mathbb {S}^{4m+4}$. Specifically, the defining equations in (3.11) give the initial value problem
 \begin{equation} \begin{gathered}
\frac{\dot{f_1}}{f_1} =\frac{\dot{f_2}}{f_2},\quad
f_1^2+(\dot{f_1})^2=1,\\ f_1(0) =f_2(0)=0,\quad
\dot{f_1}(0)=\dot{f_2}(0)=1, \end{gathered}
\end{equation}
\begin{equation} \begin{gathered}
\frac{\dot{f_1}}{f_1} =\frac{\dot{f_2}}{f_2},\quad
f_1^2+(\dot{f_1})^2=1,\\ f_1(0) =f_2(0)=0,\quad
\dot{f_1}(0)=\dot{f_2}(0)=1, \end{gathered}
\end{equation}in the original coordinates. The solution is exactly the standard sphere metric
We define ![]() $\zeta _\infty$ to be the integral curve that emanates from
$\zeta _\infty$ to be the integral curve that emanates from ![]() $p_1^+$ and lies in
$p_1^+$ and lies in ![]() $\mathcal {C}_{\Lambda \geq 0}\cap \{H=1\}$. We have
$\mathcal {C}_{\Lambda \geq 0}\cap \{H=1\}$. We have
As studied in [Reference ChiChi21], the integral curve ![]() $\zeta _\infty$ is known to be defined on
$\zeta _\infty$ is known to be defined on ![]() $\mathbb {R}$; it joins
$\mathbb {R}$; it joins ![]() $p_1^+$ and
$p_1^+$ and ![]() $p_2^+$ and represents a complete non-trivial Ricci-flat metric defined on
$p_2^+$ and represents a complete non-trivial Ricci-flat metric defined on ![]() $\mathbb {R}^{4m+4}$.
$\mathbb {R}^{4m+4}$.
As shown in the following proposition, there exists an integral curve that joins ![]() $p_0^+$ and
$p_0^+$ and ![]() $p_1^-$, and it represents the standard quaternionic Kähler metric on
$p_1^-$, and it represents the standard quaternionic Kähler metric on ![]() $\mathbb {HP}^{m+1}$. By the
$\mathbb {HP}^{m+1}$. By the ![]() $\mathbb {Z}_2$-symmetry of (2.7) on the sign of
$\mathbb {Z}_2$-symmetry of (2.7) on the sign of ![]() $(X_1,X_2)$, we know that there also exists an integral curve that emanates from
$(X_1,X_2)$, we know that there also exists an integral curve that emanates from ![]() $p_1^+$ and tends to
$p_1^+$ and tends to ![]() $p_0^-$, and it represents the standard quaternionic Kähler metric on
$p_0^-$, and it represents the standard quaternionic Kähler metric on ![]() $\overline {\mathbb {HP}}^{m+1}$.
$\overline {\mathbb {HP}}^{m+1}$.
Proposition 3.5 The integral curve ![]() $\gamma _{0}$ lies on the one-dimensional invariant set
$\gamma _{0}$ lies on the one-dimensional invariant set
The integral curve ![]() $\zeta _{ {1}/({2m+6})}$ lies on the one-dimensional invariant set
$\zeta _{ {1}/({2m+6})}$ lies on the one-dimensional invariant set
Proof. As ![]() $X_1-X_2=Y-Z$ and
$X_1-X_2=Y-Z$ and ![]() $X_2=-Z$ on
$X_2=-Z$ on ![]() $\mathcal {B}_{QK}$, we can eliminate
$\mathcal {B}_{QK}$, we can eliminate ![]() $X_1$ and
$X_1$ and ![]() $X_2$ in (2.9). Hence,
$X_2$ in (2.9). Hence,
holds on ![]() $\mathcal {B}_{QK}$. Therefore,
$\mathcal {B}_{QK}$. Therefore,
 \begin{align} & \langle\nabla(X_2+Z),V\rangle|_{\mathcal{B}_{QK}} \nonumber\\ &\quad =(X_2+Z)H\left(G+\frac{1}{n}(1-H^2)\right)-\frac{1}{n}(1-H^2)-X_2H+(4m+8)YZ-6Z^2+Z(X_1-2X_2) \nonumber\\ &\quad =-\frac{1}{n}(1-H^2)-X_2H+(4m+8)YZ-6Z^2+Z(X_1-2X_2) \nonumber\\ &\quad =\frac{1}{n-1}\left(\frac{12m}{n}(Z-Y)^2+6Y^2+4m(4m+8)YZ-12mZ^2-\frac{n-1}{n}\right) \nonumber\\ &\qquad \text {eliminating} X_1 {\rm and} X_2 {\rm by the definition of} {\mathcal{B}_{QK}} \nonumber\\ &\quad =0 \quad \text{by (3.14)}. \end{align}
\begin{align} & \langle\nabla(X_2+Z),V\rangle|_{\mathcal{B}_{QK}} \nonumber\\ &\quad =(X_2+Z)H\left(G+\frac{1}{n}(1-H^2)\right)-\frac{1}{n}(1-H^2)-X_2H+(4m+8)YZ-6Z^2+Z(X_1-2X_2) \nonumber\\ &\quad =-\frac{1}{n}(1-H^2)-X_2H+(4m+8)YZ-6Z^2+Z(X_1-2X_2) \nonumber\\ &\quad =\frac{1}{n-1}\left(\frac{12m}{n}(Z-Y)^2+6Y^2+4m(4m+8)YZ-12mZ^2-\frac{n-1}{n}\right) \nonumber\\ &\qquad \text {eliminating} X_1 {\rm and} X_2 {\rm by the definition of} {\mathcal{B}_{QK}} \nonumber\\ &\quad =0 \quad \text{by (3.14)}. \end{align}On the other hand, we have
 \begin{align} & \langle\nabla(X_1-X_2+Z-Y),V\rangle|_{\mathcal{B}_{QK}} \nonumber\\ &\quad =(X_1-X_2+Z-Y)\left(H\left(G+\frac{1}{n}(1-H^2)-1\right)+4Z-2Y\right)+(n-1)(X_2+Z)(Z-Y) \nonumber\\ &\quad =0. \end{align}
\begin{align} & \langle\nabla(X_1-X_2+Z-Y),V\rangle|_{\mathcal{B}_{QK}} \nonumber\\ &\quad =(X_1-X_2+Z-Y)\left(H\left(G+\frac{1}{n}(1-H^2)-1\right)+4Z-2Y\right)+(n-1)(X_2+Z)(Z-Y) \nonumber\\ &\quad =0. \end{align}
Therefore, the set ![]() $\mathcal {B}_{QK}$ is indeed invariant.
$\mathcal {B}_{QK}$ is indeed invariant.
Since ![]() $X_1=Y-2Z$ and
$X_1=Y-2Z$ and ![]() $X_2=-Z$ on
$X_2=-Z$ on ![]() $\mathcal {B}_{QK}$, one can realize
$\mathcal {B}_{QK}$, one can realize ![]() $\mathcal {B}_{QK}$ as a hyperbola (3.14). Note that
$\mathcal {B}_{QK}$ as a hyperbola (3.14). Note that ![]() $p_0^+$ and
$p_0^+$ and ![]() $p_1^-$ are the only critical points in
$p_1^-$ are the only critical points in ![]() $\mathcal {B}_{QK}$ and they are in the same connected component in (3.14). Therefore, there is an integral curve that joins
$\mathcal {B}_{QK}$ and they are in the same connected component in (3.14). Therefore, there is an integral curve that joins ![]() $p_0^+$ and
$p_0^+$ and ![]() $p_1^-$ and lies on
$p_1^-$ and lies on ![]() $\mathcal {B}_{QK}$. Hence, the integral curve must be some
$\mathcal {B}_{QK}$. Hence, the integral curve must be some ![]() $\gamma _{s_1}$. Let
$\gamma _{s_1}$. Let ![]() $v(\eta )$ be the normalized velocity of the linearized solution that uniquely corresponds to
$v(\eta )$ be the normalized velocity of the linearized solution that uniquely corresponds to ![]() $\gamma _0$. It is clear that
$\gamma _0$. It is clear that ![]() $\lim _{\eta \to -\infty }v(\eta )= {v_1}/{\|v_1\|}$ is tangent to
$\lim _{\eta \to -\infty }v(\eta )= {v_1}/{\|v_1\|}$ is tangent to ![]() $\mathcal {B}_{QK}$ at
$\mathcal {B}_{QK}$ at ![]() $p_0^+$. Hence, we know that
$p_0^+$. Hence, we know that ![]() $\gamma _0$ lies on
$\gamma _0$ lies on ![]() $\mathcal {B}_{QK}$. By the
$\mathcal {B}_{QK}$. By the ![]() $\mathbb {Z}_2$-symmetry on the sign of
$\mathbb {Z}_2$-symmetry on the sign of ![]() $(X_1,X_2)$, we know that
$(X_1,X_2)$, we know that ![]() $\zeta _{ {1}/({2m+6})}$ lies on the invariant set
$\zeta _{ {1}/({2m+6})}$ lies on the invariant set
and joins ![]() $p_1^+$ and
$p_1^+$ and ![]() $p_0^-$.
$p_0^-$.
Remark 3.6 The defining equations for ![]() $\mathcal {B}_{QK}$ are equivalent to the dynamical system
$\mathcal {B}_{QK}$ are equivalent to the dynamical system
 \begin{equation} \begin{aligned} & \frac{\dot{f_1}}{f_1}=-2\frac{f_1}{f_2^2}+\frac{1}{f_1},\\ & \frac{\dot{f_2}}{f_2}=-\frac{f_1}{f_2^2}.\\ \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \frac{\dot{f_1}}{f_1}=-2\frac{f_1}{f_2^2}+\frac{1}{f_1},\\ & \frac{\dot{f_2}}{f_2}=-\frac{f_1}{f_2^2}.\\ \end{aligned} \end{equation}
While ![]() $f_1(0)=0$ and
$f_1(0)=0$ and ![]() $\dot {f_1}(0)=1$ can be obtained from the coordinate of
$\dot {f_1}(0)=1$ can be obtained from the coordinate of ![]() $p_0^+$, the initial conditions
$p_0^+$, the initial conditions ![]() $f_2(0)$ and
$f_2(0)$ and ![]() $\dot {f_2}(0)$ are obtained from
$\dot {f_2}(0)$ are obtained from ![]() $v_1$. Specifically, from (3.1) we have
$v_1$. Specifically, from (3.1) we have
 \[ f_2(0)=\lim_{\eta\to-\infty}\left(\frac{\sqrt{1-H^2}}{n\sqrt{YZ}}\right) (\gamma_0(\eta))=\sqrt{\frac{4(m+3)}{n}},\quad \dot{f_2}(0)=\lim_{\eta\to-\infty}\left(\frac{X_2}{\sqrt{YZ}}\right)(\gamma_0(\eta))=0. \]
\[ f_2(0)=\lim_{\eta\to-\infty}\left(\frac{\sqrt{1-H^2}}{n\sqrt{YZ}}\right) (\gamma_0(\eta))=\sqrt{\frac{4(m+3)}{n}},\quad \dot{f_2}(0)=\lim_{\eta\to-\infty}\left(\frac{X_2}{\sqrt{YZ}}\right)(\gamma_0(\eta))=0. \]
Solving the initial value problem, the standard quaternionic Kähler metric on ![]() $\mathbb {HP}^{m+1}$ is
$\mathbb {HP}^{m+1}$ is
Finally, we consider the linearization at ![]() $p_2^+$. We have
$p_2^+$. We have
 \[ \begin{bmatrix}
-\dfrac{16m^2+8m-6}{n^2} & \dfrac{16m(m+1)}{n^2} &
(8m+12)z_0 & 8mz_0\\ \dfrac{12m+12}{n^2} &
-\dfrac{4m+6}{n^2} & 4(m+2)z_0 & 4(2m+1)(m+3)z_0\\
-\dfrac{4m(2m+3)z_0}{n} & \dfrac{4m(2m+3)z_0}{n} & 0 & 0\\
\dfrac{(4m+6)z_0}{n} & -\dfrac{(4m+6)z_0}{n} & 0 & 0
\end{bmatrix}. \]
\[ \begin{bmatrix}
-\dfrac{16m^2+8m-6}{n^2} & \dfrac{16m(m+1)}{n^2} &
(8m+12)z_0 & 8mz_0\\ \dfrac{12m+12}{n^2} &
-\dfrac{4m+6}{n^2} & 4(m+2)z_0 & 4(2m+1)(m+3)z_0\\
-\dfrac{4m(2m+3)z_0}{n} & \dfrac{4m(2m+3)z_0}{n} & 0 & 0\\
\dfrac{(4m+6)z_0}{n} & -\dfrac{(4m+6)z_0}{n} & 0 & 0
\end{bmatrix}. \]
Eigenvalues and eigenvectors are
 \begin{gather*}
\delta_1=-\frac{2m+1-\sqrt{(2m+1)^2-8(2m+3)(m+1)n^2z_0^2}}{n},\\
\delta_2=-\frac{2m+1+\sqrt{(2m+1)^2-8(2m+3)(m+1)n^2z_0^2}}{n},\\
\delta_3=\frac{2}{n},\quad \delta_4=0;\\
u_1=\begin{bmatrix} \dfrac{2mn}{2m+3}\delta_1\\
-\dfrac{3n}{2(2m+3)}\delta_1\\ -2mnz_0\\ nz_0
\end{bmatrix},\quad u_2=\begin{bmatrix}
\dfrac{2mn}{2m+3}\delta_2\\ -\dfrac{3n}{2(2m+3)}\delta_2\\
-2mnz_0\\ nz_0 \end{bmatrix},\\ u_3=\begin{bmatrix} -1\\
-1\\ 0\\ 0 \end{bmatrix},\quad u_4=\begin{bmatrix}
-2n((2m+3)^2+2m)z_0\\ -2n((2m+3)^2+2m)z_0\\ 2m+3\\ 1
\end{bmatrix}. \end{gather*}
\begin{gather*}
\delta_1=-\frac{2m+1-\sqrt{(2m+1)^2-8(2m+3)(m+1)n^2z_0^2}}{n},\\
\delta_2=-\frac{2m+1+\sqrt{(2m+1)^2-8(2m+3)(m+1)n^2z_0^2}}{n},\\
\delta_3=\frac{2}{n},\quad \delta_4=0;\\
u_1=\begin{bmatrix} \dfrac{2mn}{2m+3}\delta_1\\
-\dfrac{3n}{2(2m+3)}\delta_1\\ -2mnz_0\\ nz_0
\end{bmatrix},\quad u_2=\begin{bmatrix}
\dfrac{2mn}{2m+3}\delta_2\\ -\dfrac{3n}{2(2m+3)}\delta_2\\
-2mnz_0\\ nz_0 \end{bmatrix},\\ u_3=\begin{bmatrix} -1\\
-1\\ 0\\ 0 \end{bmatrix},\quad u_4=\begin{bmatrix}
-2n((2m+3)^2+2m)z_0\\ -2n((2m+3)^2+2m)z_0\\ 2m+3\\ 1
\end{bmatrix}. \end{gather*}
The first three eigenvectors are tangent to ![]() $\mathcal {E}$. Furthermore, the first two eigenvectors are tangent to
$\mathcal {E}$. Furthermore, the first two eigenvectors are tangent to ![]() $\mathcal {E}\cap \{H=1\}$ and
$\mathcal {E}\cap \{H=1\}$ and ![]() $\delta _2<\delta _1<0$. For
$\delta _2<\delta _1<0$. For ![]() $m\geq 1$, the critical point
$m\geq 1$, the critical point ![]() $p_2^+$ is a stable node for the restricted system on
$p_2^+$ is a stable node for the restricted system on ![]() $\mathcal {E}\cap \{H=1\}$. Let
$\mathcal {E}\cap \{H=1\}$. Let ![]() $\Phi$ be the only integral curve that emanates from
$\Phi$ be the only integral curve that emanates from ![]() $p_2^+$. It converges to
$p_2^+$. It converges to ![]() $p_2^-$ and lies on the one-dimensional invariant set
$p_2^-$ and lies on the one-dimensional invariant set
Remark 3.7 The initial value problem from the defining equations (3.18) is similar to the one from (3.11). Specifically, we have
 \begin{equation} \begin{gathered} f_1^2
=\frac{1}{2m+3}f_2^2,\quad
\frac{(2m+1)(2m+3)^2}{2m+(2m+3)^2}(f_1^2+(\dot{f_1})^2)=1,\\
f_1(0) =f_2(0)=0,\quad
\dot{f_1}(0)=\frac{1}{\sqrt{2m+3}}\dot{f_2}(0)=\frac{1}{2m+3}
\sqrt{\frac{2m+(2m+3)^2}{2m+1}}. \end{gathered}
\end{equation}
\begin{equation} \begin{gathered} f_1^2
=\frac{1}{2m+3}f_2^2,\quad
\frac{(2m+1)(2m+3)^2}{2m+(2m+3)^2}(f_1^2+(\dot{f_1})^2)=1,\\
f_1(0) =f_2(0)=0,\quad
\dot{f_1}(0)=\frac{1}{\sqrt{2m+3}}\dot{f_2}(0)=\frac{1}{2m+3}
\sqrt{\frac{2m+(2m+3)^2}{2m+1}}. \end{gathered}
\end{equation}
Hence, ![]() $\Phi$ represents the sine cone over Jensen's sphere
$\Phi$ represents the sine cone over Jensen's sphere
 \begin{align*} g&=dt^2+\frac{2m+(2m+3)^2}{(2m+1)(2m+3)^2}\sin^2(t)g_{\mathbb{S}^{4m+3}}|_{\mathfrak{p}_1}+ \frac{2m+(2m+3)^2}{(2m+1)(2m+3)}\sin^2(t) g_{\mathbb{S}^{4m+3}}|_{\mathfrak{p}_2}\\ &=dt^2+\sin^2(t)g_{\mathrm{Jensen}}. \end{align*}
\begin{align*} g&=dt^2+\frac{2m+(2m+3)^2}{(2m+1)(2m+3)^2}\sin^2(t)g_{\mathbb{S}^{4m+3}}|_{\mathfrak{p}_1}+ \frac{2m+(2m+3)^2}{(2m+1)(2m+3)}\sin^2(t) g_{\mathbb{S}^{4m+3}}|_{\mathfrak{p}_2}\\ &=dt^2+\sin^2(t)g_{\mathrm{Jensen}}. \end{align*}
4. Existence of the first Einstein metric
We prove the existence of a heterocline that joins ![]() $p_0^\pm$ in this section. The technique is to construct a compact set
$p_0^\pm$ in this section. The technique is to construct a compact set ![]() $\mathcal {S}$ such that a
$\mathcal {S}$ such that a ![]() $\gamma _{s_1}$ that enters the set can only escape through points in
$\gamma _{s_1}$ that enters the set can only escape through points in ![]() $\mathcal {E} \cap \{H\geq 0\}\cap \{X_1-X_2=0\}$. Then we apply Lemma 4.4 in [Reference BöhmBöh98] to complete the proof.
$\mathcal {E} \cap \{H\geq 0\}\cap \{X_1-X_2=0\}$. Then we apply Lemma 4.4 in [Reference BöhmBöh98] to complete the proof.
We define the compact set ![]() $\mathcal {S}$ as follows. Define polynomials
$\mathcal {S}$ as follows. Define polynomials
 \begin{equation} \begin{aligned} A & :=YX_2-\frac{3}{m} Z\left(X_1+\frac{2m}{3} X_2\right),\\ B & :=\frac{1-H^2}{n}-\frac{2n^2(2m+3)(m-1)}{m(2m+1)(8m+3)} YZ,\\ P & :=X_1\left(R_2-\frac{1}{n}(1-H^2)\right)-X_2 \left(R_1-\frac{1}{n}(1-H^2)\right)-2X_2\left(X_1+\frac{2m}{3}X_2\right)(X_1-X_2),\\ Q & :=-4X_2Y^2-(4m+8)(4mX_2+2X_1)YZ+(2X_1+(4m+2)X_2)\frac{1-H^2}{n}\\ & \quad +4X_2\left(X_1+\frac{2m}{3}X_2\right)\left(H+\frac{2m}{3}X_2\right). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} A & :=YX_2-\frac{3}{m} Z\left(X_1+\frac{2m}{3} X_2\right),\\ B & :=\frac{1-H^2}{n}-\frac{2n^2(2m+3)(m-1)}{m(2m+1)(8m+3)} YZ,\\ P & :=X_1\left(R_2-\frac{1}{n}(1-H^2)\right)-X_2 \left(R_1-\frac{1}{n}(1-H^2)\right)-2X_2\left(X_1+\frac{2m}{3}X_2\right)(X_1-X_2),\\ Q & :=-4X_2Y^2-(4m+8)(4mX_2+2X_1)YZ+(2X_1+(4m+2)X_2)\frac{1-H^2}{n}\\ & \quad +4X_2\left(X_1+\frac{2m}{3}X_2\right)\left(H+\frac{2m}{3}X_2\right). \end{aligned} \end{equation}Define
The following proposition lists some basic properties of ![]() $\mathcal {S}$.
$\mathcal {S}$.
Proposition 4.1 The set ![]() $\mathcal {S}$ has the following properties.
$\mathcal {S}$ has the following properties.
(i) For
 $m\geq 1$, the set
$m\geq 1$, the set  $\mathcal {S}\cap \{X_2=0\}$ is a union of
$\mathcal {S}\cap \{X_2=0\}$ is a union of  $\{p_0^+\}$ and a one-dimensional curve
$\{p_0^+\}$ and a one-dimensional curve  $\Gamma :=\mathcal {S}\cap \{X_1=X_2=0\}$. For
$\Gamma :=\mathcal {S}\cap \{X_1=X_2=0\}$. For  $m\geq 2$, the set
$m\geq 2$, the set  $\Gamma$ is bounded.
$\Gamma$ is bounded.(ii) The variable
 $Y$ is positive in
$Y$ is positive in  $\mathcal {S}$ for
$\mathcal {S}$ for  $m\geq 1$.
$m\geq 1$.(iii) For
 $m\geq 1$, the set
$m\geq 1$, the set  $\mathcal {S}\cap \{Z=0\}$ is
$\mathcal {S}\cap \{Z=0\}$ is  $\{p_0^+, (0,0,\sqrt { ({n-1})/{6n}},0)\}$.
$\{p_0^+, (0,0,\sqrt { ({n-1})/{6n}},0)\}$.(iv) The set
 $\mathcal {S}$ is compact for
$\mathcal {S}$ is compact for  $m\geq 2$.
$m\geq 2$.
Proof. Since ![]() $A\geq 0$ in
$A\geq 0$ in ![]() $\mathcal {S}$, a point in
$\mathcal {S}$, a point in ![]() $\mathcal {S}$ with vanishing
$\mathcal {S}$ with vanishing ![]() $X_2$-coordinate must have
$X_2$-coordinate must have ![]() $ZX_1=0$. If we further assume
$ZX_1=0$. If we further assume ![]() $Z=0$ at that point, then from
$Z=0$ at that point, then from ![]() $P\geq 0$ we have
$P\geq 0$ we have ![]() $X_1(1-H^2)=X_1(1-9X_1^2)\leq 0$. Hence, we obtain
$X_1(1-H^2)=X_1(1-9X_1^2)\leq 0$. Hence, we obtain ![]() $X_1=\frac {1}{3}$ and that point must be
$X_1=\frac {1}{3}$ and that point must be ![]() $p_0^+$. We obtain
$p_0^+$. We obtain ![]() $\Gamma$ if
$\Gamma$ if ![]() $X_1=0$ is further assumed.
$X_1=0$ is further assumed.
It is obvious that ![]() $\Gamma =\mathcal {E}\cap \{X_1=X_2=0\}$ for
$\Gamma =\mathcal {E}\cap \{X_1=X_2=0\}$ for ![]() $m=1$ and the set is non-compact. We prove that
$m=1$ and the set is non-compact. We prove that ![]() $\Gamma$ is bounded for
$\Gamma$ is bounded for ![]() $m\geq 2$. From
$m\geq 2$. From ![]() $B\geq 0$ and (2.9), we have
$B\geq 0$ and (2.9), we have
 \begin{align} & 6Y^2+4m(4m+8)YZ-12mZ^2=\frac{n-1}{n}\geq (n-1)\frac{2n^2(2m+3)(m-1)}{m(2m+1)(8m+3)}YZ \nonumber\\ &\quad \Leftrightarrow 6Y^2+\left(4m(4m+8)-(n-1)\frac{2n^2(2m+3)(m-1)}{m(2m+1)(8m+3)}\right)YZ-12mZ^2\geq 0. \end{align}
\begin{align} & 6Y^2+4m(4m+8)YZ-12mZ^2=\frac{n-1}{n}\geq (n-1)\frac{2n^2(2m+3)(m-1)}{m(2m+1)(8m+3)}YZ \nonumber\\ &\quad \Leftrightarrow 6Y^2+\left(4m(4m+8)-(n-1)\frac{2n^2(2m+3)(m-1)}{m(2m+1)(8m+3)}\right)YZ-12mZ^2\geq 0. \end{align}
For ![]() $m\geq 2$, the inequality above implies
$m\geq 2$, the inequality above implies ![]() $mY-Z\geq 0$. Then from (2.9) we have
$mY-Z\geq 0$. Then from (2.9) we have ![]() $ ({n-1})/{n}\geq 6Y^2+(4m+32)Z^2$. The first claim is clear.
$ ({n-1})/{n}\geq 6Y^2+(4m+32)Z^2$. The first claim is clear.
Suppose there is a point in ![]() $\mathcal {S}$ with vanishing
$\mathcal {S}$ with vanishing ![]() $Y$-coordinate. From
$Y$-coordinate. From ![]() $A\geq 0$ we know that
$A\geq 0$ we know that ![]() $- ({3}/{m})Z(X_1+ ({2m}/{3})X_2)=0$ at that point. If
$- ({3}/{m})Z(X_1+ ({2m}/{3})X_2)=0$ at that point. If ![]() $Z\neq 0$, then
$Z\neq 0$, then ![]() $X_1=X_2=Y=0$ at that point, which is impossible from (2.9). If
$X_1=X_2=Y=0$ at that point, which is impossible from (2.9). If ![]() $X_1+ ({2m}/{3})X_2\neq 0$, then
$X_1+ ({2m}/{3})X_2\neq 0$, then ![]() $Y=Z=0$ at that point. Then from (2.9), we have
$Y=Z=0$ at that point. Then from (2.9), we have ![]() $X_1-X_2\neq 0$. From
$X_1-X_2\neq 0$. From ![]() $P\geq 0$ we know that
$P\geq 0$ we know that ![]() $- ({1}/{n})(1-H^2)-2X_2(X_1+ ({2m}/{3})X_2)\geq 0$ at that point. The point has to be
$- ({1}/{n})(1-H^2)-2X_2(X_1+ ({2m}/{3})X_2)\geq 0$ at that point. The point has to be ![]() $(\frac {1}{3},0,0,0)$, which does not lie on
$(\frac {1}{3},0,0,0)$, which does not lie on ![]() $\mathcal {E}$. The above discussion proves the second claim.
$\mathcal {E}$. The above discussion proves the second claim.
Since ![]() $P\geq 0$ on a point with vanishing
$P\geq 0$ on a point with vanishing ![]() $Z$-coordinate in
$Z$-coordinate in ![]() $\mathcal {S}$, we have
$\mathcal {S}$, we have
By the definition of ![]() $\mathcal {S}$, each term in the above inequality is non-positive. Since
$\mathcal {S}$, each term in the above inequality is non-positive. Since ![]() $Y>0$ from the second claim, the variable
$Y>0$ from the second claim, the variable ![]() $X_2$ must vanish and the third claim is clear.
$X_2$ must vanish and the third claim is clear.
Finally, from ![]() $A\geq 0$ and
$A\geq 0$ and ![]() $X_1-X_2\geq 0$ in
$X_1-X_2\geq 0$ in ![]() $\mathcal {S}$, we know that
$\mathcal {S}$, we know that ![]() $X_2(Y- (({2m+3})/{m})Z)\geq 0$ in
$X_2(Y- (({2m+3})/{m})Z)\geq 0$ in ![]() $\mathcal {S}$. If
$\mathcal {S}$. If ![]() $X_2\neq 0$, then
$X_2\neq 0$, then ![]() $mY\geq (2m+3)Z$ and the boundedness of all variables is obtained from (2.9). If
$mY\geq (2m+3)Z$ and the boundedness of all variables is obtained from (2.9). If ![]() $X_2=0$, then the boundedness comes from the first claim. Hence,
$X_2=0$, then the boundedness comes from the first claim. Hence, ![]() $\mathcal {S}$ is a compact set.
$\mathcal {S}$ is a compact set.
The case ![]() $m=1$ is very special. In the following proposition, we show that for
$m=1$ is very special. In the following proposition, we show that for ![]() $m=1$, the defining inequalities
$m=1$, the defining inequalities ![]() $A\geq 0$ and
$A\geq 0$ and ![]() $P\geq 0$ must be equalities. The set
$P\geq 0$ must be equalities. The set ![]() $\mathcal {S}$ is closely related to the integral curves
$\mathcal {S}$ is closely related to the integral curves ![]() $\gamma _\infty$ in Remark 3.2 and
$\gamma _\infty$ in Remark 3.2 and ![]() $\Phi$ in Remark 3.7.
$\Phi$ in Remark 3.7.
Proposition 4.2 For ![]() $m=1$, the set
$m=1$, the set ![]() $\mathcal {S}$ is the union
$\mathcal {S}$ is the union
Proof. Consider ![]() $\mathcal {S}$ with
$\mathcal {S}$ with ![]() $m=1$. If
$m=1$. If ![]() $X_2=0$ is imposed, we obtain either the point
$X_2=0$ is imposed, we obtain either the point ![]() $p_0^+$ or
$p_0^+$ or ![]() $\Gamma$ from Proposition 4.1(a). Hence, we assume
$\Gamma$ from Proposition 4.1(a). Hence, we assume ![]() $X_2>0$ in the following. From
$X_2>0$ in the following. From ![]() $A\geq 0$ it is clear that
$A\geq 0$ it is clear that ![]() $X_2(Y-5Z)\geq YX_2-3Z(X_1+\frac {2}{3}X_2)\geq 0$ and hence
$X_2(Y-5Z)\geq YX_2-3Z(X_1+\frac {2}{3}X_2)\geq 0$ and hence ![]() $Y-5Z\geq 0$.
$Y-5Z\geq 0$.
One can easily verify that
If ![]() $X_1=X_2=X>0$, the first two terms in (4.3) vanish while the last term is non-positive. Then we must have
$X_1=X_2=X>0$, the first two terms in (4.3) vanish while the last term is non-positive. Then we must have ![]() $A=0$, from which we deduce
$A=0$, from which we deduce ![]() $Y-5Z= 0$. By (3.18) we obtain the line segment
$Y-5Z= 0$. By (3.18) we obtain the line segment ![]() $\Phi \cap \{X_1,X_2> 0\}$.
$\Phi \cap \{X_1,X_2> 0\}$.
For ![]() $X_1\neq X_2$, we rewrite (4.3) as follows:
$X_1\neq X_2$, we rewrite (4.3) as follows:
The last two terms in (4.4) are non-positive. Hence, from ![]() $P\geq 0$ we have
$P\geq 0$ we have
 \begin{align} 0&\leq 6YZ-2X_2\big(X_1+\tfrac{2}{3}X_2\big)-\tfrac{10}{147}(1-H^2) \nonumber\\ &= 6YZ-2X_2\big(X_1+\tfrac{2}{3}X_2\big)-\tfrac{10}{147} \big(\tfrac{7}{6}\big(6Y^2+48YZ-12Z^2+\tfrac{12}{7}(X_1-X_2)^2\big)-H^2\big) \nonumber\\ &\quad \text{by (2.9)} \nonumber\\ &= \tfrac{1}{21}(5X_1+4X_2+5Y+2Z)(X_1-X_2-Y+5Z) \nonumber\\ &\quad +\tfrac{1}{21}(5X_1+4X_2-5Y-2Z)(X_1-X_2+Y-5Z). \end{align}
\begin{align} 0&\leq 6YZ-2X_2\big(X_1+\tfrac{2}{3}X_2\big)-\tfrac{10}{147}(1-H^2) \nonumber\\ &= 6YZ-2X_2\big(X_1+\tfrac{2}{3}X_2\big)-\tfrac{10}{147} \big(\tfrac{7}{6}\big(6Y^2+48YZ-12Z^2+\tfrac{12}{7}(X_1-X_2)^2\big)-H^2\big) \nonumber\\ &\quad \text{by (2.9)} \nonumber\\ &= \tfrac{1}{21}(5X_1+4X_2+5Y+2Z)(X_1-X_2-Y+5Z) \nonumber\\ &\quad +\tfrac{1}{21}(5X_1+4X_2-5Y-2Z)(X_1-X_2+Y-5Z). \end{align}
Suppose ![]() $X_1-X_2-Y+5Z\leq 0$; then the first term in the last line of (4.5) is non-positive. As the summation above is non-negative, we know that the second term in the last line of (4.5) must be non-negative. As
$X_1-X_2-Y+5Z\leq 0$; then the first term in the last line of (4.5) is non-positive. As the summation above is non-negative, we know that the second term in the last line of (4.5) must be non-negative. As ![]() $X_1-X_2+Y-5Z\geq 0$, we must have
$X_1-X_2+Y-5Z\geq 0$, we must have ![]() $\frac {1}{5}(5X_1+4X_2-2Z)\geq Y$. From
$\frac {1}{5}(5X_1+4X_2-2Z)\geq Y$. From ![]() $A\geq 0$ we have
$A\geq 0$ we have
Then we claim that the first term in (4.3) is non-positive since
 \begin{align} 6YZ-2X_2\big(X_1+\tfrac{2}{3}X_2\big)&\leq \tfrac{6}{5}(5X_1+4X_2-2Z)Z-2X_2\big(X_1+\tfrac{2}{3}X_2\big) \nonumber\\ &\leq \tfrac{2}{5}\big(5X_1+4X_2-\tfrac{2}{3}X_2\big)X_2-2X_2\big(X_1+\tfrac{2}{3}X_2\big) \nonumber\\ &=0. \end{align}
\begin{align} 6YZ-2X_2\big(X_1+\tfrac{2}{3}X_2\big)&\leq \tfrac{6}{5}(5X_1+4X_2-2Z)Z-2X_2\big(X_1+\tfrac{2}{3}X_2\big) \nonumber\\ &\leq \tfrac{2}{5}\big(5X_1+4X_2-\tfrac{2}{3}X_2\big)X_2-2X_2\big(X_1+\tfrac{2}{3}X_2\big) \nonumber\\ &=0. \end{align}
But ![]() $P\geq 0$. Hence, assumptions
$P\geq 0$. Hence, assumptions ![]() $X_1\neq X_2$ and
$X_1\neq X_2$ and ![]() $X_1-X_2-Y+5Z\leq 0$ lead to the vanishing of
$X_1-X_2-Y+5Z\leq 0$ lead to the vanishing of ![]() $A$ and
$A$ and ![]() $P$.
$P$.
Suppose ![]() $X_1-X_2-Y+5Z\geq 0$. Then
$X_1-X_2-Y+5Z\geq 0$. Then ![]() $A\geq 0$ implies
$A\geq 0$ implies
Then we claim that the first term in (4.3) is also non-positive since
 \begin{align} 6YZ-2X_2\big(X_1+\tfrac{2}{3}X_2\big)&\leq 6(X_1-X_2+5Z)Z-2X_2\big(X_1+\tfrac{2}{3}X_2\big) \nonumber\\ &\leq 2\big(X_1-X_2+\tfrac{5}{3}X_2\big)X_2-2X_2\big(X_1+\tfrac{2}{3}X_2\big) \nonumber\\ &=0. \end{align}
\begin{align} 6YZ-2X_2\big(X_1+\tfrac{2}{3}X_2\big)&\leq 6(X_1-X_2+5Z)Z-2X_2\big(X_1+\tfrac{2}{3}X_2\big) \nonumber\\ &\leq 2\big(X_1-X_2+\tfrac{5}{3}X_2\big)X_2-2X_2\big(X_1+\tfrac{2}{3}X_2\big) \nonumber\\ &=0. \end{align}
Hence, the assumption ![]() $X_1\neq X_2$ and
$X_1\neq X_2$ and ![]() $X_1-X_2-Y+5Z\geq 0$ also leads to the vanishing of
$X_1-X_2-Y+5Z\geq 0$ also leads to the vanishing of ![]() $A$ and
$A$ and ![]() $P$.
$P$.
Therefore, points in ![]() $\mathcal {S}$ with
$\mathcal {S}$ with ![]() $X_1\neq X_2$ must have vanished
$X_1\neq X_2$ must have vanished ![]() $A$ and
$A$ and ![]() $P$, which leads to the equalities
$P$, which leads to the equalities
Note that the last two equations above are equivalent to the defining equations in (3.4) for ![]() $m=1$. We obtain
$m=1$. We obtain ![]() $\gamma _\infty$ and critical points
$\gamma _\infty$ and critical points ![]() $p_0^+$ and
$p_0^+$ and ![]() $p_2^+$.
$p_2^+$.
Remark 4.3 For ![]() $m=1$, there is another heterocline
$m=1$, there is another heterocline ![]() $\chi$ that also lies on the invariant set
$\chi$ that also lies on the invariant set ![]() $\mathcal {B}_{\mathrm {Spin}(7)}$. The integral curve joins
$\mathcal {B}_{\mathrm {Spin}(7)}$. The integral curve joins ![]() $q_3^+$ and
$q_3^+$ and ![]() $p_2^+$. Note that from the proof to Proposition 4.2, it is clear that
$p_2^+$. Note that from the proof to Proposition 4.2, it is clear that ![]() $X_1-X_2$ and
$X_1-X_2$ and ![]() $Y-5Z$ are positive along
$Y-5Z$ are positive along ![]() $\gamma _\infty$. These two polynomials are negative along
$\gamma _\infty$. These two polynomials are negative along ![]() $\chi$ and hence the integral curve is not in
$\chi$ and hence the integral curve is not in ![]() $\mathcal {S}$.
$\mathcal {S}$.
With Proposition 4.2 established, we can take ![]() $m=1$ as our ‘initial case’ for further analysis of cases with
$m=1$ as our ‘initial case’ for further analysis of cases with ![]() $m>1$. In particular, we prove the following technical proposition.
$m>1$. In particular, we prove the following technical proposition.
Proposition 4.4 For ![]() $m\geq 1$, the inequality
$m\geq 1$, the inequality ![]() $Q\geq 0$ holds on the set
$Q\geq 0$ holds on the set ![]() $\mathcal {S}\cap \{P=0\}$. For
$\mathcal {S}\cap \{P=0\}$. For ![]() $m=1$, the inequality reaches equality only at
$m=1$, the inequality reaches equality only at ![]() $\{p_0^+, p_2^+\} \cup \gamma _\infty \cup \Gamma$. For
$\{p_0^+, p_2^+\} \cup \gamma _\infty \cup \Gamma$. For ![]() $m\geq 2$, the inequality reaches equality only at
$m\geq 2$, the inequality reaches equality only at ![]() $p_0^+$, a point on
$p_0^+$, a point on ![]() $\Phi$, and points in
$\Phi$, and points in ![]() $\Gamma$.
$\Gamma$.
Proof. We consider ![]() $\mathcal {S}\cap \{P=0\}$ as a union of slices
$\mathcal {S}\cap \{P=0\}$ as a union of slices
Note that each ![]() $\mathcal {L}_\kappa$ contains
$\mathcal {L}_\kappa$ contains ![]() $\Gamma$. As
$\Gamma$. As ![]() $X_1\geq X_2\geq 0$ in
$X_1\geq X_2\geq 0$ in ![]() $\mathcal {S}$, the function
$\mathcal {S}$, the function ![]() $Q$ vanishes once
$Q$ vanishes once ![]() $X_1$ does. We assume
$X_1$ does. We assume ![]() $X_1>0$ in the following discussion.
$X_1>0$ in the following discussion.
For ![]() $\mathcal {L}_0$, we have
$\mathcal {L}_0$, we have
From ![]() $A\geq 0$ we have
$A\geq 0$ we have ![]() $Z=0$. Then
$Z=0$. Then ![]() $Q|_{\mathcal {L}_0}=2X_1 (({1-H^2})/{n})$, and
$Q|_{\mathcal {L}_0}=2X_1 (({1-H^2})/{n})$, and ![]() $P=0$ becomes
$P=0$ becomes ![]() $-X_1 (({1-H^2})/{n})=0$. Hence,
$-X_1 (({1-H^2})/{n})=0$. Hence, ![]() $\mathcal {L}_0=\Gamma \cup \{p_0^+\}$ and
$\mathcal {L}_0=\Gamma \cup \{p_0^+\}$ and ![]() $Q|_{\mathcal {L}_0}= 0$.
$Q|_{\mathcal {L}_0}= 0$.
If ![]() $\kappa =1$, let
$\kappa =1$, let ![]() $X:=X_1=X_2>0$. Then
$X:=X_1=X_2>0$. Then ![]() $A\geq 0$ and
$A\geq 0$ and ![]() $P= 0$ respectively become
$P= 0$ respectively become
For ![]() $X>0$ we must have
$X>0$ we must have ![]() $Y= (2m+3)Z$. Then from (2.9) we find that
$Y= (2m+3)Z$. Then from (2.9) we find that ![]() $Y=(2m+3)Z= (2m+3)z_0$. Hence,
$Y=(2m+3)Z= (2m+3)z_0$. Hence, ![]() $\mathcal {L}_1$ is a union of
$\mathcal {L}_1$ is a union of ![]() $\Gamma$ and a part of the invariant set (3.18). More specifically, from
$\Gamma$ and a part of the invariant set (3.18). More specifically, from ![]() $B\geq 0$ we have
$B\geq 0$ we have
and it follows that
 \begin{equation} \mathcal{L}_1=\Gamma \cup \left(\Phi \cap \left\{0< X\leq \frac{1}{n}\sqrt{\frac{36m^3+90m^2+117m+54}{m(8m+3)(4m^2+14m+9)}}\leq \frac{1}{n}\right\}\right) \end{equation}
\begin{equation} \mathcal{L}_1=\Gamma \cup \left(\Phi \cap \left\{0< X\leq \frac{1}{n}\sqrt{\frac{36m^3+90m^2+117m+54}{m(8m+3)(4m^2+14m+9)}}\leq \frac{1}{n}\right\}\right) \end{equation}
for ![]() $m\geq 2$. For
$m\geq 2$. For ![]() $m=1$, we have
$m=1$, we have
And ![]() $Q|_{\mathcal {L}_1}$ becomes
$Q|_{\mathcal {L}_1}$ becomes
 \begin{align} & Q|_{\mathcal{L}_1}
\nonumber\\ &\quad
=X\left(\!-4Y^2-(4m+8)(4m+2)YZ+(n+1)\left(\frac{1}{n}-nX^2\right)+4\left(1+\frac{2m}{3}\right)
\left(n+\frac{2m}{3}\right)X^2\right) \nonumber\\ &\quad =
X\left(\!-4(2m+3)^2z_0^2-(4m+8)(4m+2)(2m+3)z_0^2+\frac{n+1}{n}-\frac{4}{9}m(8m+3)X^2\right)
\nonumber\\ &\quad =
\frac{4}{9}m(8m+3)X\left(\frac{1}{n^2}\frac{36m^3+90m^2+117m+54}{m(8m+3)(4m^2+14m+9)}-X^2\right)
\nonumber\\ &\quad \geq 0.
\end{align}
\begin{align} & Q|_{\mathcal{L}_1}
\nonumber\\ &\quad
=X\left(\!-4Y^2-(4m+8)(4m+2)YZ+(n+1)\left(\frac{1}{n}-nX^2\right)+4\left(1+\frac{2m}{3}\right)
\left(n+\frac{2m}{3}\right)X^2\right) \nonumber\\ &\quad =
X\left(\!-4(2m+3)^2z_0^2-(4m+8)(4m+2)(2m+3)z_0^2+\frac{n+1}{n}-\frac{4}{9}m(8m+3)X^2\right)
\nonumber\\ &\quad =
\frac{4}{9}m(8m+3)X\left(\frac{1}{n^2}\frac{36m^3+90m^2+117m+54}{m(8m+3)(4m^2+14m+9)}-X^2\right)
\nonumber\\ &\quad \geq 0.
\end{align}
Hence, for ![]() $m\geq 1$, the function
$m\geq 1$, the function ![]() $Q|_{\mathcal {L}_1}\geq 0$ and it only vanishes on
$Q|_{\mathcal {L}_1}\geq 0$ and it only vanishes on ![]() $\Gamma$ and boundary points of
$\Gamma$ and boundary points of ![]() $\mathcal {L}_1\cap \Phi$. Note that for
$\mathcal {L}_1\cap \Phi$. Note that for ![]() $m=1$, one of the boundary points of
$m=1$, one of the boundary points of ![]() $\mathcal {L}_1\cap \Phi$ is
$\mathcal {L}_1\cap \Phi$ is ![]() $p_2^+$.
$p_2^+$.
For each ![]() $\mathcal {L}_\kappa$ with
$\mathcal {L}_\kappa$ with ![]() $\kappa \in (0,1)$, replace
$\kappa \in (0,1)$, replace ![]() $X_2$ with
$X_2$ with ![]() $X_1\kappa$. Then (2.9) and
$X_1\kappa$. Then (2.9) and ![]() $P= 0$ respectively become
$P= 0$ respectively become
 \begin{equation} \begin{aligned} & \frac{n-1}{n}-\frac{12m}{n}(1-\kappa)^2X_1^2=6Y^2+4m(4m+8)YZ-12mZ^2,\\ & \frac{\kappa-1}{n}-\frac{\kappa-1}{3n}(32\kappa^2m^2-12\kappa^2m+ 48m\kappa-18\kappa+27)X_1^2\\ & \quad = 2\kappa Y^2-(4m+8)YZ+(4m\kappa+6)Z^2. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \frac{n-1}{n}-\frac{12m}{n}(1-\kappa)^2X_1^2=6Y^2+4m(4m+8)YZ-12mZ^2,\\ & \frac{\kappa-1}{n}-\frac{\kappa-1}{3n}(32\kappa^2m^2-12\kappa^2m+ 48m\kappa-18\kappa+27)X_1^2\\ & \quad = 2\kappa Y^2-(4m+8)YZ+(4m\kappa+6)Z^2. \end{aligned} \end{equation} With the equations above, we can write the constant ![]() $1$ as a homogeneous polynomial
$1$ as a homogeneous polynomial ![]() $One(Y,Z)$ of degree
$One(Y,Z)$ of degree ![]() $2$. Multiplying the constant term in
$2$. Multiplying the constant term in ![]() $B$ by
$B$ by ![]() $One(Y, Z)$, the function
$One(Y, Z)$, the function ![]() $B$ restricted to each
$B$ restricted to each ![]() $\mathcal {L}_\kappa \cap \{P=0\}$ then becomes a homogeneous polynomial in
$\mathcal {L}_\kappa \cap \{P=0\}$ then becomes a homogeneous polynomial in ![]() $Y$ and
$Y$ and ![]() $Z$. Factor out
$Z$. Factor out ![]() $X_1$ in
$X_1$ in ![]() $Q$ and multiply the constant term in
$Q$ and multiply the constant term in ![]() $ {Q}/{X_1}$ by
$ {Q}/{X_1}$ by ![]() $One(Y,Z)$. We see that
$One(Y,Z)$. We see that ![]() $Q$ restricted on each
$Q$ restricted on each ![]() $\mathcal {L}_\kappa \cap \{P=0\}$ is a homogeneous polynomial in
$\mathcal {L}_\kappa \cap \{P=0\}$ is a homogeneous polynomial in ![]() $X_1$,
$X_1$, ![]() $Y$ and
$Y$ and ![]() $Z$. In summary, we have
$Z$. In summary, we have
 \begin{equation} \begin{aligned} A|_{\mathcal{L}_\kappa\cap \{P=0\}} & =X_1\left(Y\kappa-\frac{3}{m}Z\left(1+\frac{2m}{3}\kappa\right)\right),\\ B|_{\mathcal{L}_\kappa\cap \{P=0\}} & =b_2Z^2+b_1YZ+b_0Y^2,\\ Q|_{\mathcal{L}_\kappa\cap \{P=0\}} & =X_1(q_2 Z^2+q_1YZ+q_0 Y^2). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} A|_{\mathcal{L}_\kappa\cap \{P=0\}} & =X_1\left(Y\kappa-\frac{3}{m}Z\left(1+\frac{2m}{3}\kappa\right)\right),\\ B|_{\mathcal{L}_\kappa\cap \{P=0\}} & =b_2Z^2+b_1YZ+b_0Y^2,\\ Q|_{\mathcal{L}_\kappa\cap \{P=0\}} & =X_1(q_2 Z^2+q_1YZ+q_0 Y^2). \end{aligned} \end{equation}
The coefficients ![]() $b_i$ and
$b_i$ and ![]() $q_i$ in (4.13) are rational functions in
$q_i$ in (4.13) are rational functions in ![]() $m$ and
$m$ and ![]() $\kappa$. Explicit formulas for each coefficient are presented in the Appendix for the sake of simplicity. As
$\kappa$. Explicit formulas for each coefficient are presented in the Appendix for the sake of simplicity. As ![]() $Y$ is positive in
$Y$ is positive in ![]() $\mathcal {S}$ from Proposition 4.1, we factor out
$\mathcal {S}$ from Proposition 4.1, we factor out ![]() $Y$ and consider
$Y$ and consider ![]() $A|_{\mathcal {L}_\kappa \cap \{P=0\}}=X_1Y\tilde {A}_{m,\kappa }( {Z}/{Y})$,
$A|_{\mathcal {L}_\kappa \cap \{P=0\}}=X_1Y\tilde {A}_{m,\kappa }( {Z}/{Y})$, ![]() $B|_{\mathcal {L}_\kappa \cap \{P=0\}}=Y^2\tilde {B}_{m,\kappa }( {Z}/{Y})$ and
$B|_{\mathcal {L}_\kappa \cap \{P=0\}}=Y^2\tilde {B}_{m,\kappa }( {Z}/{Y})$ and ![]() $Q|_{\mathcal {L}_\kappa \cap \{P=0\}}=X_1Y^2\tilde {Q}_{m,\kappa }( {Z}/{Y})$, where
$Q|_{\mathcal {L}_\kappa \cap \{P=0\}}=X_1Y^2\tilde {Q}_{m,\kappa }( {Z}/{Y})$, where
We have
for any ![]() $(m,\kappa )\in [1,\infty )\times (0,1)$. Therefore, the restricted function
$(m,\kappa )\in [1,\infty )\times (0,1)$. Therefore, the restricted function ![]() $Q|_{\mathcal {L}_\kappa \cap \{P=0\}}$ is non-negative if it is so on the boundary of
$Q|_{\mathcal {L}_\kappa \cap \{P=0\}}$ is non-negative if it is so on the boundary of ![]() $\mathcal {L}_\kappa \cap \{P=0\}$. The upper bound and the lower bound of
$\mathcal {L}_\kappa \cap \{P=0\}$. The upper bound and the lower bound of ![]() $ {Z}/{Y}$ on each slice are respectively provided by
$ {Z}/{Y}$ on each slice are respectively provided by ![]() $A|_{\mathcal {L}_\kappa \cap \{P=0\}}\geq 0$ and
$A|_{\mathcal {L}_\kappa \cap \{P=0\}}\geq 0$ and ![]() $B|_{\mathcal {L}_\kappa \cap \{P=0\}}\geq 0$. Specifically, from
$B|_{\mathcal {L}_\kappa \cap \{P=0\}}\geq 0$. Specifically, from ![]() $A|_{\mathcal {L}_\kappa \cap \{P=0\}}\geq 0$ we have
$A|_{\mathcal {L}_\kappa \cap \{P=0\}}\geq 0$ we have ![]() $ {Z}/{Y}\leq {m\kappa }/({3+2m\kappa })$. As shown in (A.1), we have
$ {Z}/{Y}\leq {m\kappa }/({3+2m\kappa })$. As shown in (A.1), we have ![]() $b_2<0$. By Proposition A.1 in the Appendix, the smaller real root
$b_2<0$. By Proposition A.1 in the Appendix, the smaller real root ![]() $\sigma (m,\kappa )$ of
$\sigma (m,\kappa )$ of ![]() $\tilde {B}_{m,\kappa }$ is in the interval
$\tilde {B}_{m,\kappa }$ is in the interval ![]() $(0, {m\kappa }/({3+2m\kappa }))$. Hence, from
$(0, {m\kappa }/({3+2m\kappa }))$. Hence, from ![]() $B|_{\mathcal {L}_\kappa \cap \{P=0\}}\geq 0$ we have
$B|_{\mathcal {L}_\kappa \cap \{P=0\}}\geq 0$ we have ![]() $ {Z}/{Y}\geq \sigma (m,\kappa )$. By the arbitrariness of
$ {Z}/{Y}\geq \sigma (m,\kappa )$. By the arbitrariness of ![]() $\kappa$, it is clear that the minimizing point of
$\kappa$, it is clear that the minimizing point of ![]() $Q$ on
$Q$ on ![]() ${\mathcal {S}\cap \{P=0\}}$ lies on
${\mathcal {S}\cap \{P=0\}}$ lies on ![]() $\mathcal {S}\cap \{P=0\}\cap \{A=0\}$ or
$\mathcal {S}\cap \{P=0\}\cap \{A=0\}$ or ![]() $\mathcal {S}\cap \{P=0\}\cap \{B=0\}$.
$\mathcal {S}\cap \{P=0\}\cap \{B=0\}$.
We have
 \begin{align} Q|_{\mathcal{L}_\kappa\cap \{A=0\}}&=X_1Y^2\tilde{Q}_{m,\kappa} \left(\frac{m\kappa}{3+2m\kappa}\right) \nonumber\\ &=X_1Y^2\frac{4(m+3)(m-1)(4\kappa^3m^2(8m-1)+4\kappa^2 m(8m-3)+18 \kappa m+9(1-\kappa))\kappa^2}{3(2\kappa m+3)(1-\kappa)(2\kappa^2m(8m-5)+6\kappa(4m-1)+9)} \nonumber\\ &\geq 0. \end{align}
\begin{align} Q|_{\mathcal{L}_\kappa\cap \{A=0\}}&=X_1Y^2\tilde{Q}_{m,\kappa} \left(\frac{m\kappa}{3+2m\kappa}\right) \nonumber\\ &=X_1Y^2\frac{4(m+3)(m-1)(4\kappa^3m^2(8m-1)+4\kappa^2 m(8m-3)+18 \kappa m+9(1-\kappa))\kappa^2}{3(2\kappa m+3)(1-\kappa)(2\kappa^2m(8m-5)+6\kappa(4m-1)+9)} \nonumber\\ &\geq 0. \end{align}
Therefore, for ![]() $m\geq 2$, the function
$m\geq 2$, the function ![]() $Q$ is positive on
$Q$ is positive on ![]() $\mathcal {L}_\kappa \cap \{A=0\}$ for any
$\mathcal {L}_\kappa \cap \{A=0\}$ for any ![]() $\kappa \in (0,1)$. For
$\kappa \in (0,1)$. For ![]() $m=1$, the function
$m=1$, the function ![]() $Q$ vanishes at
$Q$ vanishes at ![]() $\mathcal {S}\cap \{P=0\}\cap \{A=0\}$.
$\mathcal {S}\cap \{P=0\}\cap \{A=0\}$.
Proving the non-negativity of ![]() $Q|_{\mathcal {L}_\kappa \cap \{B=0\}\cap \{P=0\}}$ is a bit more computationally involved. From Proposition 4.2, we know that for
$Q|_{\mathcal {L}_\kappa \cap \{B=0\}\cap \{P=0\}}$ is a bit more computationally involved. From Proposition 4.2, we know that for ![]() $m=1$, the polynomials
$m=1$, the polynomials ![]() $A$,
$A$, ![]() $B$ and
$B$ and ![]() $P$ identically vanish at
$P$ identically vanish at ![]() $\gamma _\infty$. Therefore, an explicit formula for the root
$\gamma _\infty$. Therefore, an explicit formula for the root ![]() $\sigma (1,\kappa )$ can be obtained from
$\sigma (1,\kappa )$ can be obtained from ![]() $A=0$. We have
$A=0$. We have
Define the function ![]() $F(m,\kappa ):=\tilde {Q}_{m,\kappa }(\sigma (m,\kappa ))$. To show that
$F(m,\kappa ):=\tilde {Q}_{m,\kappa }(\sigma (m,\kappa ))$. To show that ![]() $Q|_{\mathcal {L}_\kappa \cap \{P=0\}\cap \{B=0\}}\geq 0$, it suffices to show that
$Q|_{\mathcal {L}_\kappa \cap \{P=0\}\cap \{B=0\}}\geq 0$, it suffices to show that ![]() $F(m,\kappa )\geq 0$ for any
$F(m,\kappa )\geq 0$ for any ![]() $(m,\kappa )\in [1,\infty )\times (0,1)$. Note that the vanishing of
$(m,\kappa )\in [1,\infty )\times (0,1)$. Note that the vanishing of ![]() $F(m,\kappa )$ means
$F(m,\kappa )$ means ![]() $\sigma (m,\kappa )$ being also a root of
$\sigma (m,\kappa )$ being also a root of ![]() $\tilde {Q}_{m,\kappa }$. From the computation (4.16) we have
$\tilde {Q}_{m,\kappa }$. From the computation (4.16) we have
for any ![]() $\kappa \in (0,1)$. Furthermore, by implicit derivative, we have
$\kappa \in (0,1)$. Furthermore, by implicit derivative, we have
 \[ \left(\frac{\partial \sigma}{\partial m}\right)(1,\kappa)= \left(-\frac{\frac{\partial b_2}{\partial m}\sigma^2+ \frac{\partial b_1}{\partial m}\sigma+\frac{\partial b_0}{\partial m}}{2b_2\sigma+b_1}\right) (1,\kappa)=-\frac{(92\kappa^4+1202\kappa^3+1458\kappa^2-367\kappa-537)\kappa}{66(3+4\kappa) (\kappa+1)(3+2\kappa)^2}, \]
\[ \left(\frac{\partial \sigma}{\partial m}\right)(1,\kappa)= \left(-\frac{\frac{\partial b_2}{\partial m}\sigma^2+ \frac{\partial b_1}{\partial m}\sigma+\frac{\partial b_0}{\partial m}}{2b_2\sigma+b_1}\right) (1,\kappa)=-\frac{(92\kappa^4+1202\kappa^3+1458\kappa^2-367\kappa-537)\kappa}{66(3+4\kappa) (\kappa+1)(3+2\kappa)^2}, \]
and it follows that
 \begin{align*} \left(\frac{\partial F}{\partial m}\right)(1,\kappa) &= \left(\frac{\partial q_2}{\partial m}\sigma^2+ \frac{\partial q_1}{\partial m}\sigma+\frac{\partial q_0}{\partial m}+2q_2\sigma \frac{\partial \sigma}{\partial m}+q_1\frac{\partial \sigma}{\partial m}\right)(1,\kappa)\\ &=\frac{4(\kappa-1)(184\kappa^2-244\kappa-339)\kappa^2}{99(3+4\kappa)(\kappa+1)(2\kappa+3)}>0. \end{align*}
\begin{align*} \left(\frac{\partial F}{\partial m}\right)(1,\kappa) &= \left(\frac{\partial q_2}{\partial m}\sigma^2+ \frac{\partial q_1}{\partial m}\sigma+\frac{\partial q_0}{\partial m}+2q_2\sigma \frac{\partial \sigma}{\partial m}+q_1\frac{\partial \sigma}{\partial m}\right)(1,\kappa)\\ &=\frac{4(\kappa-1)(184\kappa^2-244\kappa-339)\kappa^2}{99(3+4\kappa)(\kappa+1)(2\kappa+3)}>0. \end{align*}
Hence, ![]() $F\geq 0$ on a neighborhood around
$F\geq 0$ on a neighborhood around ![]() $\{(1,\kappa )\mid \kappa \in (0,1)\}\subset [1,\infty )\times (0,1)$. In other words, for an
$\{(1,\kappa )\mid \kappa \in (0,1)\}\subset [1,\infty )\times (0,1)$. In other words, for an ![]() $m$ that is slightly larger than
$m$ that is slightly larger than ![]() $1$, the root
$1$, the root ![]() $\sigma (m,\kappa )$ of
$\sigma (m,\kappa )$ of ![]() $\tilde {B}_{m,\kappa }$ is strictly between the two real roots of
$\tilde {B}_{m,\kappa }$ is strictly between the two real roots of ![]() $\tilde {Q}_{m,\kappa }$. Hence, proving
$\tilde {Q}_{m,\kappa }$. Hence, proving ![]() $F\geq 0$ on
$F\geq 0$ on ![]() $[1,\infty )\times (0,1)$ is equivalent to showing that
$[1,\infty )\times (0,1)$ is equivalent to showing that ![]() $\sigma (m,\kappa )$ stays between the two real roots of
$\sigma (m,\kappa )$ stays between the two real roots of ![]() $\tilde {Q}_{m,\kappa }$ for varying
$\tilde {Q}_{m,\kappa }$ for varying ![]() $(m,\kappa )$. This idea leads us to consider the resultant
$(m,\kappa )$. This idea leads us to consider the resultant ![]() $r(\tilde {Q}_{m,\kappa },\tilde {B}_{m,\kappa })$ for the two polynomials. We have
$r(\tilde {Q}_{m,\kappa },\tilde {B}_{m,\kappa })$ for the two polynomials. We have
 \begin{align} r(\tilde{Q}_{m,\kappa},\tilde{B}_{m,\kappa})&= -\frac{64\kappa^2(m-1)(2\kappa m+3)}{(8m+3)^2(2m+1)^2m^2(1-\kappa)(2\kappa^2m(8m-5)+ 6\kappa(4m-1)+9)^2}\tilde{r}, \nonumber\\ \tilde{r}&=262144 \kappa ^4 m^{10}+(516096 \kappa ^4+679936 \kappa ^3) m^9 \nonumber\\ &\quad +(373760\kappa ^4+1233920 \kappa ^3+675840 \kappa ^2) m^8 \nonumber\\ &\quad +(-275904 \kappa ^4+1151040 \kappa ^3+1143744 \kappa ^2+308160 \kappa ) m^7 \nonumber\\ &\quad +(-926496 \kappa ^4+248832 \kappa ^3+1432512 \kappa ^2+507456 \kappa +54432) m^6 \nonumber\\ &\quad +(-800496 \kappa ^4-1256256 \kappa ^3+1472688 \kappa ^2+857520 \kappa +92016) m^5 \nonumber\\ &\quad +(-281880 \kappa ^4-1525392 \kappa ^3+266328 \kappa ^2+1353024 \kappa +199584) m^4 \nonumber\\ &\quad +(-33048 \kappa ^4-644436 \kappa ^3-672624 \kappa ^2+957420 \kappa +375192) m^3 \nonumber\\ &\quad +(-90396 \kappa ^3-433026 \kappa ^2 +186624 \kappa +333882) m^2 \nonumber\\ &\quad +(-74358 \kappa ^2-59049 \kappa +133407) m+19683(1-\kappa). \end{align}
\begin{align} r(\tilde{Q}_{m,\kappa},\tilde{B}_{m,\kappa})&= -\frac{64\kappa^2(m-1)(2\kappa m+3)}{(8m+3)^2(2m+1)^2m^2(1-\kappa)(2\kappa^2m(8m-5)+ 6\kappa(4m-1)+9)^2}\tilde{r}, \nonumber\\ \tilde{r}&=262144 \kappa ^4 m^{10}+(516096 \kappa ^4+679936 \kappa ^3) m^9 \nonumber\\ &\quad +(373760\kappa ^4+1233920 \kappa ^3+675840 \kappa ^2) m^8 \nonumber\\ &\quad +(-275904 \kappa ^4+1151040 \kappa ^3+1143744 \kappa ^2+308160 \kappa ) m^7 \nonumber\\ &\quad +(-926496 \kappa ^4+248832 \kappa ^3+1432512 \kappa ^2+507456 \kappa +54432) m^6 \nonumber\\ &\quad +(-800496 \kappa ^4-1256256 \kappa ^3+1472688 \kappa ^2+857520 \kappa +92016) m^5 \nonumber\\ &\quad +(-281880 \kappa ^4-1525392 \kappa ^3+266328 \kappa ^2+1353024 \kappa +199584) m^4 \nonumber\\ &\quad +(-33048 \kappa ^4-644436 \kappa ^3-672624 \kappa ^2+957420 \kappa +375192) m^3 \nonumber\\ &\quad +(-90396 \kappa ^3-433026 \kappa ^2 +186624 \kappa +333882) m^2 \nonumber\\ &\quad +(-74358 \kappa ^2-59049 \kappa +133407) m+19683(1-\kappa). \end{align}
As verified in Proposition A.2 in the Appendix, the inequality ![]() $r(\tilde {Q}_{m,\kappa },\tilde {B}_{m,\kappa }) \leq 0$ is valid for any
$r(\tilde {Q}_{m,\kappa },\tilde {B}_{m,\kappa }) \leq 0$ is valid for any ![]() $(m,\kappa )\in [1,\infty )\times (0,1)$. Furthermore, the function
$(m,\kappa )\in [1,\infty )\times (0,1)$. Furthermore, the function ![]() $r(\tilde {Q}_{m,\kappa },\tilde {B}_{m,\kappa })$ vanishes if and only if
$r(\tilde {Q}_{m,\kappa },\tilde {B}_{m,\kappa })$ vanishes if and only if ![]() $m=1$. In particular, both
$m=1$. In particular, both ![]() $\tilde {Q}_{1,\kappa }$ and
$\tilde {Q}_{1,\kappa }$ and ![]() $\tilde {B}_{1,\kappa }$ have
$\tilde {B}_{1,\kappa }$ have ![]() $\sigma (1,\kappa )= {\kappa }/({2\kappa +3})$ as their roots. For
$\sigma (1,\kappa )= {\kappa }/({2\kappa +3})$ as their roots. For ![]() $m>1$, the polynomials
$m>1$, the polynomials ![]() $\tilde {Q}_{m,\kappa }$ and
$\tilde {Q}_{m,\kappa }$ and ![]() $\tilde {B}_{m,\kappa }$ do not share any common root. Hence,
$\tilde {B}_{m,\kappa }$ do not share any common root. Hence, ![]() $F\geq 0$ on
$F\geq 0$ on ![]() $[1,\infty )\times (0,1)$ and the function
$[1,\infty )\times (0,1)$ and the function ![]() $F$ vanishes if and only if
$F$ vanishes if and only if ![]() $m=1$. Therefore, for
$m=1$. Therefore, for ![]() $m\geq 2$, the inequality
$m\geq 2$, the inequality ![]() $Q|_{\mathcal {L}_\kappa \cap \{P=0\}\cap \{B=0\}}\geq 0$ is valid and the equality occurs only at
$Q|_{\mathcal {L}_\kappa \cap \{P=0\}\cap \{B=0\}}\geq 0$ is valid and the equality occurs only at ![]() $p_0^+$ and a point
$p_0^+$ and a point ![]() $\Phi \cap \{B=0\}$. The proof is complete.
$\Phi \cap \{B=0\}$. The proof is complete.
With the help of the proceeding proposition, we are ready to prove the following lemma.
Lemma 4.5 For ![]() $m\geq 2$, integral curves
$m\geq 2$, integral curves ![]() $\gamma _{s_1}$ that are in the interior of
$\gamma _{s_1}$ that are in the interior of ![]() $\mathcal {S}$ can only escape through some point in
$\mathcal {S}$ can only escape through some point in ![]() $\mathcal {E}\cap \{H\geq 0\}\cap \{X_1-X_2=0\}$.
$\mathcal {E}\cap \{H\geq 0\}\cap \{X_1-X_2=0\}$.
Proof. The boundary ![]() $\partial \mathcal {S}$ is a union of the following five sets:
$\partial \mathcal {S}$ is a union of the following five sets:
By Proposition 4.1, if a ![]() $\gamma _{s_1}$ escapes
$\gamma _{s_1}$ escapes ![]() $\mathcal {S}$ through some point with vanished
$\mathcal {S}$ through some point with vanished ![]() $X_2$-coordinate, the point must lie in
$X_2$-coordinate, the point must lie in ![]() $\mathcal {S}\cap \{A=0\}\cap \{P=0\}$. Hence, we aim to show that
$\mathcal {S}\cap \{A=0\}\cap \{P=0\}$. Hence, we aim to show that ![]() $V$ points inward when restricted to the last three parts of
$V$ points inward when restricted to the last three parts of ![]() $\partial \mathcal {S}$.
$\partial \mathcal {S}$.
A straightforward computation shows that
 \begin{align} & \langle\nabla
A,V\rangle|_{A=0} \nonumber\\ &\quad
=A\left(2H\left(G+\frac{1}{n}(1-H^2)\right)-2X_1-(4m+2)X_2\right)
\nonumber\\ &\qquad
+\frac{A}{X_1+(2m/3)X_2}\left(R_1+\frac{2m}{3}R_2-\left(1+\frac{2m}{3}\right)
\frac{1}{n}(1-H^2)\right) +\frac{Y}{X_1+(2m/3)X_2}P
\nonumber\\ &\quad =\frac{Y}{X_1+(2m/3)X_2}P\quad
\text{since $A=0$} \nonumber\\ &\quad \geq 0.
\end{align}
\begin{align} & \langle\nabla
A,V\rangle|_{A=0} \nonumber\\ &\quad
=A\left(2H\left(G+\frac{1}{n}(1-H^2)\right)-2X_1-(4m+2)X_2\right)
\nonumber\\ &\qquad
+\frac{A}{X_1+(2m/3)X_2}\left(R_1+\frac{2m}{3}R_2-\left(1+\frac{2m}{3}\right)
\frac{1}{n}(1-H^2)\right) +\frac{Y}{X_1+(2m/3)X_2}P
\nonumber\\ &\quad =\frac{Y}{X_1+(2m/3)X_2}P\quad
\text{since $A=0$} \nonumber\\ &\quad \geq 0.
\end{align}
It is confirmed that ![]() $V|_{A=0}$ points to the interior of
$V|_{A=0}$ points to the interior of ![]() $\mathcal {S}$.
$\mathcal {S}$.
Since
 \begin{align} & \langle\nabla B,V\rangle|_{B=0} \nonumber\\ &\quad =-2\frac{H}{n}(H^2-1)\left(G+\frac{1}{n}(1-H^2)\right) \nonumber\\ &\qquad -\frac{2n^2(2m+3)(m-1)}{m(16m^2+14m+3)}YZ \left(2H\left(G+\frac{1}{n}(1-H^2)\right)-2X_2\right) \nonumber\\ &\qquad \text{by (2.11)} \nonumber\\ &\quad =2BH\left(G+\frac{1}{n}(1-H^2)\right)+\frac{4n^2(2m+3)(m-1)}{m(16m^2+14m+3)}YZ X_2 \nonumber\\ &\quad =\frac{4n^2(2m+3)(m-1)}{m(16m^2+14m+3)}YZ X_2\quad \text{since $B=0$} \nonumber\\ &\quad \geq 0, \end{align}
\begin{align} & \langle\nabla B,V\rangle|_{B=0} \nonumber\\ &\quad =-2\frac{H}{n}(H^2-1)\left(G+\frac{1}{n}(1-H^2)\right) \nonumber\\ &\qquad -\frac{2n^2(2m+3)(m-1)}{m(16m^2+14m+3)}YZ \left(2H\left(G+\frac{1}{n}(1-H^2)\right)-2X_2\right) \nonumber\\ &\qquad \text{by (2.11)} \nonumber\\ &\quad =2BH\left(G+\frac{1}{n}(1-H^2)\right)+\frac{4n^2(2m+3)(m-1)}{m(16m^2+14m+3)}YZ X_2 \nonumber\\ &\quad =\frac{4n^2(2m+3)(m-1)}{m(16m^2+14m+3)}YZ X_2\quad \text{since $B=0$} \nonumber\\ &\quad \geq 0, \end{align}
it is clear that ![]() $V|_{B=0}$ points to the interior of
$V|_{B=0}$ points to the interior of ![]() $\mathcal {S}$.
$\mathcal {S}$.
Since
 \begin{align} & \langle\nabla P,V\rangle|_{P=0} \nonumber\\ &\quad =P\left(H\left(3G+\frac{3}{n} (1-H^2)-1\right)+\frac{4m}{3}X_2\right)+(X_1-X_2)Q \nonumber\\ &\quad =(X_1-X_2)Q \quad \text{since $P=0$} \nonumber\\ &\quad \geq 0 \quad \text{by Proposition (4.4)}, \end{align}
\begin{align} & \langle\nabla P,V\rangle|_{P=0} \nonumber\\ &\quad =P\left(H\left(3G+\frac{3}{n} (1-H^2)-1\right)+\frac{4m}{3}X_2\right)+(X_1-X_2)Q \nonumber\\ &\quad =(X_1-X_2)Q \quad \text{since $P=0$} \nonumber\\ &\quad \geq 0 \quad \text{by Proposition (4.4)}, \end{align}
we learn that ![]() $V|_{P=0}$ also points to the interior of
$V|_{P=0}$ also points to the interior of ![]() $\mathcal {S}$.
$\mathcal {S}$.
Finally, we need to exclude the possibility of non-transversal passing of a ![]() $\gamma _{s_1}$ through some point with
$\gamma _{s_1}$ through some point with ![]() $X_1\neq X_2$. By (4.19) and Proposition 4.1, such a point does not exist on
$X_1\neq X_2$. By (4.19) and Proposition 4.1, such a point does not exist on ![]() $\mathcal {S}\cap \{B=0\}$. Suppose there were such a point on
$\mathcal {S}\cap \{B=0\}$. Suppose there were such a point on ![]() $\mathcal {S}\cap \{P=0\}$; then
$\mathcal {S}\cap \{P=0\}$; then ![]() $P=Q=0$ at that point by (4.20). Then by Proposition 4.4, we know that such a point is either
$P=Q=0$ at that point by (4.20). Then by Proposition 4.4, we know that such a point is either ![]() $p_0^+$ or a point on
$p_0^+$ or a point on ![]() $\Phi$, which is impossible. Suppose the non-transversal passing point exists on
$\Phi$, which is impossible. Suppose the non-transversal passing point exists on ![]() $\mathcal {S}\cap \{A=0\}$; then by (4.18) and Proposition 4.1, we must have
$\mathcal {S}\cap \{A=0\}$; then by (4.18) and Proposition 4.1, we must have ![]() $A=P=0$ at that point, which is also impossible.
$A=P=0$ at that point, which is also impossible.
To show that some ![]() $\gamma _{s_1}$ is initially in the set
$\gamma _{s_1}$ is initially in the set ![]() $\mathcal {S}$ we need the following technical proposition.
$\mathcal {S}$ we need the following technical proposition.
Proposition 4.6 Define ![]() $\check {A}:=YX_2- (({m+2})/{m})Z(X_1+ ({2m}/{3})X_2)$. For
$\check {A}:=YX_2- (({m+2})/{m})Z(X_1+ ({2m}/{3})X_2)$. For ![]() $m\geq 2$, the function
$m\geq 2$, the function ![]() $Q$ is positive on the set
$Q$ is positive on the set
Proof. We consider ![]() $\check {\mathcal {S}}$ as a union of slices
$\check {\mathcal {S}}$ as a union of slices
For each ![]() $\check {\mathcal {L}}_\kappa$ with
$\check {\mathcal {L}}_\kappa$ with ![]() $\kappa \in (0,1)$, replace
$\kappa \in (0,1)$, replace ![]() $X_2$ with
$X_2$ with ![]() $\kappa X_1$. Then from (2.9) and
$\kappa X_1$. Then from (2.9) and ![]() $P< 0$ we have
$P< 0$ we have
 \begin{align} 0&> \left(\frac{1-\kappa}{3n}(32\kappa^2m^2-12\kappa^2m+48m\kappa-18\kappa+27)- \frac{12m}{n(n-1)}(1-\kappa)^3\right)X_1^2 \nonumber\\ &\quad -\left(2\kappa+\frac{6(1-\kappa)}{n-1}\right)Y^2+(4m+8) \left(1-4m\frac{1-\kappa}{n-1}\right)YZ+\left(\frac{1-\kappa}{n-1}12m-(4m\kappa+6)\right)Z^2 \nonumber\\ &= \frac{(1-\kappa)(16\kappa^2m^2-10\kappa^2 m+24\kappa m-6\kappa+9)}{6m+3}X_1^2 \nonumber\\ &\quad -\left(2\kappa+\frac{6(1-\kappa)}{n-1}\right)Y^2+(4m+8)\left(1-4m\frac{1-\kappa}{n-1}\right)YZ+ \left(\frac{1-\kappa}{n-1}12m-(4m\kappa+6)\right)Z^2. \end{align}
\begin{align} 0&> \left(\frac{1-\kappa}{3n}(32\kappa^2m^2-12\kappa^2m+48m\kappa-18\kappa+27)- \frac{12m}{n(n-1)}(1-\kappa)^3\right)X_1^2 \nonumber\\ &\quad -\left(2\kappa+\frac{6(1-\kappa)}{n-1}\right)Y^2+(4m+8) \left(1-4m\frac{1-\kappa}{n-1}\right)YZ+\left(\frac{1-\kappa}{n-1}12m-(4m\kappa+6)\right)Z^2 \nonumber\\ &= \frac{(1-\kappa)(16\kappa^2m^2-10\kappa^2 m+24\kappa m-6\kappa+9)}{6m+3}X_1^2 \nonumber\\ &\quad -\left(2\kappa+\frac{6(1-\kappa)}{n-1}\right)Y^2+(4m+8)\left(1-4m\frac{1-\kappa}{n-1}\right)YZ+ \left(\frac{1-\kappa}{n-1}12m-(4m\kappa+6)\right)Z^2. \end{align}
The coefficient for ![]() $X_1^2$ in (4.21) is obviously positive for any
$X_1^2$ in (4.21) is obviously positive for any ![]() $(m,\kappa )\in [2,\infty )\times (0,1)$. On the other hand, use (2.9) to replace the constant term in
$(m,\kappa )\in [2,\infty )\times (0,1)$. On the other hand, use (2.9) to replace the constant term in ![]() $Q$ with homogeneous polynomials in
$Q$ with homogeneous polynomials in ![]() $X_1$,
$X_1$, ![]() $Y$ and
$Y$ and ![]() $Z$. The polynomial
$Z$. The polynomial ![]() $Q$ restricted on
$Q$ restricted on ![]() $\check {\mathcal {L}}_\kappa$ becomes
$\check {\mathcal {L}}_\kappa$ becomes
 \begin{align} Q|_{\check{\mathcal{L}}_\kappa} &= \frac{-64\kappa^3 m^3+(40\kappa-96)\kappa^2 m^2+ (36\kappa^2+60\kappa-108)\kappa m+54(\kappa-1)}{18m+9}X_1^3 \nonumber\\ &\quad +X_1\left(\left(2\kappa+\frac{6}{2m+1}\right)Y^2- \frac{8m+16}{2m+1}YZ-\left(12m\kappa + \frac{12 m}{2m+1}\right)Z^2\right). \end{align}
\begin{align} Q|_{\check{\mathcal{L}}_\kappa} &= \frac{-64\kappa^3 m^3+(40\kappa-96)\kappa^2 m^2+ (36\kappa^2+60\kappa-108)\kappa m+54(\kappa-1)}{18m+9}X_1^3 \nonumber\\ &\quad +X_1\left(\left(2\kappa+\frac{6}{2m+1}\right)Y^2- \frac{8m+16}{2m+1}YZ-\left(12m\kappa + \frac{12 m}{2m+1}\right)Z^2\right). \end{align}
It is obvious that the coefficient for ![]() $X_1^3$ in (4.22) is negative for any
$X_1^3$ in (4.22) is negative for any ![]() $(m,\kappa )\in [2,\infty )\times (0,1)$. Note that if (4.21) reaches equality, then one can write
$(m,\kappa )\in [2,\infty )\times (0,1)$. Note that if (4.21) reaches equality, then one can write ![]() $X_1^2$ as a homogeneous polynomial in
$X_1^2$ as a homogeneous polynomial in ![]() $Y$ and
$Y$ and ![]() $Z$. Moreover, substituting the
$Z$. Moreover, substituting the ![]() $X_1^2$ by the homogeneous polynomial in (4.22) gives the formula for
$X_1^2$ by the homogeneous polynomial in (4.22) gives the formula for ![]() $X_1Y^2\tilde {Q}( {Z}/{Y})$ as in (4.14). Therefore, from (4.21) we obtain
$X_1Y^2\tilde {Q}( {Z}/{Y})$ as in (4.14). Therefore, from (4.21) we obtain
Note that ![]() $\tilde {Q}( {Z}/{Y})$ above is defined on
$\tilde {Q}( {Z}/{Y})$ above is defined on ![]() $\check {\mathcal {S}}$ instead of
$\check {\mathcal {S}}$ instead of ![]() $\mathcal {S}\cap \{P=0\}$. On the other hand, the inequalities
$\mathcal {S}\cap \{P=0\}$. On the other hand, the inequalities ![]() $A> 0$ and
$A> 0$ and ![]() $\check {A}< 0$ become
$\check {A}< 0$ become
As shown in (4.15), it is clear that the coefficient ![]() $q_2$ is negative. It suffices to show that
$q_2$ is negative. It suffices to show that ![]() $\tilde {Q}$ is positive at
$\tilde {Q}$ is positive at ![]() $ {m\kappa }/({3+2m\kappa })$ and
$ {m\kappa }/({3+2m\kappa })$ and ![]() $ {3m\kappa }/({3(m+2)+2m(m+2)\kappa })$ to prove that the polynomial is positive on the open interval in between. From (4.16) it is clear that
$ {3m\kappa }/({3(m+2)+2m(m+2)\kappa })$ to prove that the polynomial is positive on the open interval in between. From (4.16) it is clear that ![]() $\tilde {Q}( {m\kappa }/({3+2m\kappa }))>0$. For any
$\tilde {Q}( {m\kappa }/({3+2m\kappa }))>0$. For any ![]() $(m,\kappa )\in [2,\infty )\times (0,1)$, a straightforward computation shows that
$(m,\kappa )\in [2,\infty )\times (0,1)$, a straightforward computation shows that

The proof is complete.
We are ready to prove the following lemma.
Lemma 4.7 For ![]() $m\geq 2$, the integral curve
$m\geq 2$, the integral curve ![]() $\gamma _{s_1}$ is initially in the interior of
$\gamma _{s_1}$ is initially in the interior of ![]() $\mathcal {S}$ if
$\mathcal {S}$ if ![]() $s_1\in ( {3}/({m-1}), {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)})$.
$s_1\in ( {3}/({m-1}), {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)})$.
Proof. With the linearized solution (3.1), we have
 \begin{align}
X_1(\gamma_{s_1}) & =\frac{1}{3}-(8m^2+18m+18+(4m+8)ms_1)
e^{({2}/{3})\eta}+O(e^{({2}/{3}+\epsilon)\eta}),\nonumber\\
X_2(\gamma_{s_1}) &
=(-9+3s_1(m+2))e^{({2}/{3})\eta}+O(e^{({2}/{3}+\epsilon)\eta}),\\
A(\gamma_{s_1}) & =
\frac{m+3}{m}((m-1)s_1-3)e^{({2}/{3})\eta}+
O(e^{({2}/{3}+\epsilon)\eta}),\nonumber\\
B(\gamma_{s_1}) & = \frac{2n^2(2m+3)(m-1)}{m(2m+1)(8m+3)}
\left(\frac{9(5m+3)(4m^2+4m+3)}{n^2(2m+3)(m-1)}-s_1\right)
e^{({2}/{3})\eta}+O(e^{({2}/{3}+\epsilon)\eta}),\nonumber\\
P(\gamma_{s_1}) & =
O(e^{({2}/{3}+\epsilon)\eta}),\nonumber\\
Q(\gamma_{s_1}) & =
O(e^{({2}/{3}+\epsilon)\eta}),
\end{align}
\begin{align}
X_1(\gamma_{s_1}) & =\frac{1}{3}-(8m^2+18m+18+(4m+8)ms_1)
e^{({2}/{3})\eta}+O(e^{({2}/{3}+\epsilon)\eta}),\nonumber\\
X_2(\gamma_{s_1}) &
=(-9+3s_1(m+2))e^{({2}/{3})\eta}+O(e^{({2}/{3}+\epsilon)\eta}),\\
A(\gamma_{s_1}) & =
\frac{m+3}{m}((m-1)s_1-3)e^{({2}/{3})\eta}+
O(e^{({2}/{3}+\epsilon)\eta}),\nonumber\\
B(\gamma_{s_1}) & = \frac{2n^2(2m+3)(m-1)}{m(2m+1)(8m+3)}
\left(\frac{9(5m+3)(4m^2+4m+3)}{n^2(2m+3)(m-1)}-s_1\right)
e^{({2}/{3})\eta}+O(e^{({2}/{3}+\epsilon)\eta}),\nonumber\\
P(\gamma_{s_1}) & =
O(e^{({2}/{3}+\epsilon)\eta}),\nonumber\\
Q(\gamma_{s_1}) & =
O(e^{({2}/{3}+\epsilon)\eta}),
\end{align}
near ![]() $p_0^+$. Hence, functions
$p_0^+$. Hence, functions ![]() $X_2$,
$X_2$, ![]() $A$ and
$A$ and ![]() $B$ are positive along
$B$ are positive along ![]() $\gamma _{s_1}$ near
$\gamma _{s_1}$ near ![]() $p_0^+$ if
$p_0^+$ if ![]() $s_1\in ( {3}/({m-1}), {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)})$. Furthermore, the last two equalities in (4.24) show that
$s_1\in ( {3}/({m-1}), {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)})$. Furthermore, the last two equalities in (4.24) show that ![]() $\nabla P$ and
$\nabla P$ and ![]() $\nabla Q$ are perpendicular to the linearized solution (3.1) at
$\nabla Q$ are perpendicular to the linearized solution (3.1) at ![]() $p_0$. Hence, the integral curve
$p_0$. Hence, the integral curve ![]() $\gamma _{s_1}$ is tangent to
$\gamma _{s_1}$ is tangent to ![]() $\{P=0\}$ and
$\{P=0\}$ and ![]() $\{Q=0\}$ for any
$\{Q=0\}$ for any ![]() $s_1$. It takes a little bit more work to show that the function
$s_1$. It takes a little bit more work to show that the function ![]() $P$ is initially positive along
$P$ is initially positive along ![]() $\gamma _{s_1}$. Recall in (4.20), we have
$\gamma _{s_1}$. Recall in (4.20), we have
Note that
 \begin{align*} & \left(H\left(3G+\frac{3}{n}(1-H^2)-1\right)+\frac{4m}{3}X_2\right)(\gamma_{s_1})\\ &\quad =-(48m^2+84m+20m(m+2)s_1)e^{({2}/{3})\eta}+O(e^{({2}/{3}+\epsilon)\eta}) \end{align*}
\begin{align*} & \left(H\left(3G+\frac{3}{n}(1-H^2)-1\right)+\frac{4m}{3}X_2\right)(\gamma_{s_1})\\ &\quad =-(48m^2+84m+20m(m+2)s_1)e^{({2}/{3})\eta}+O(e^{({2}/{3}+\epsilon)\eta}) \end{align*}
near ![]() $p_0^+$. If
$p_0^+$. If ![]() $P$ were negative initially along
$P$ were negative initially along ![]() $\gamma _{s_1}$ near
$\gamma _{s_1}$ near ![]() $p_0^+$, the first term in (4.25) would be positive. Moreover, from the linearized solution (3.1), we have
$p_0^+$, the first term in (4.25) would be positive. Moreover, from the linearized solution (3.1), we have
Since ![]() $ {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)}< {6(m+1)}/{(m+2)(m-1)}$ for
$ {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)}< {6(m+1)}/{(m+2)(m-1)}$ for ![]() $m\geq 2$, we know that
$m\geq 2$, we know that ![]() $\check {A}(\gamma _{s_1})$ is initially negative along
$\check {A}(\gamma _{s_1})$ is initially negative along ![]() $\gamma _{s_1}$. Based on the assumption that
$\gamma _{s_1}$. Based on the assumption that ![]() $P$ is initially negative along
$P$ is initially negative along ![]() $\gamma _{s_1}$, we know that
$\gamma _{s_1}$, we know that ![]() $\gamma _{s_1}$ is initially in
$\gamma _{s_1}$ is initially in ![]() $\check {\mathcal {S}}$. By Proposition 4.6, we know that the second term in (4.25) is also positive and so is
$\check {\mathcal {S}}$. By Proposition 4.6, we know that the second term in (4.25) is also positive and so is ![]() $P'$, which is a contradiction. Therefore, the function
$P'$, which is a contradiction. Therefore, the function ![]() $P$ must be positive initially along
$P$ must be positive initially along ![]() $\gamma _{s_1}$ near
$\gamma _{s_1}$ near ![]() $p_0^+$.
$p_0^+$.
According to § 4 in [Reference BöhmBöh98], the existence of the heterocline that joins ![]() $p_0^\pm$ relies on the number of critical points of
$p_0^\pm$ relies on the number of critical points of ![]() $\sqrt { {Z}/{Y}}$ that appear before the turning point. The number is originally denoted by
$\sqrt { {Z}/{Y}}$ that appear before the turning point. The number is originally denoted by ![]() $\sharp C_w(\bar {h})$ in [Reference BöhmBöh98], where
$\sharp C_w(\bar {h})$ in [Reference BöhmBöh98], where ![]() $w$ is the ratio
$w$ is the ratio ![]() $ {f_1}/{f_2}=\sqrt { {Z}/{Y}}$ and
$ {f_1}/{f_2}=\sqrt { {Z}/{Y}}$ and ![]() $\bar {h}$ corresponds to the initial data
$\bar {h}$ corresponds to the initial data ![]() $f$ in (2.3). We introduce the following modified definitions of
$f$ in (2.3). We introduce the following modified definitions of ![]() $\sharp C_w(\bar {h})$ and
$\sharp C_w(\bar {h})$ and ![]() $W$-intersection points.
$W$-intersection points.
Definition 4.8 For a ![]() $\gamma _{s_1}$ that is not a heterocline (i.e., a
$\gamma _{s_1}$ that is not a heterocline (i.e., a ![]() $\gamma _{s_1}$ that is not defined on
$\gamma _{s_1}$ that is not defined on ![]() $\mathbb {R}$ or
$\mathbb {R}$ or ![]() $\lim _{\eta \to \infty }\gamma _{s_1}\neq p_0^-$), let
$\lim _{\eta \to \infty }\gamma _{s_1}\neq p_0^-$), let ![]() $\sharp C(\gamma _{s_1})$ be the number of critical points of the function
$\sharp C(\gamma _{s_1})$ be the number of critical points of the function ![]() $\sqrt { {Z}/{Y}}$ along
$\sqrt { {Z}/{Y}}$ along ![]() $\gamma _{s_1}$ that appear in
$\gamma _{s_1}$ that appear in ![]() $\mathcal {E}\cap \{H>0\}\cap \{Y-Z> 0\}$.
$\mathcal {E}\cap \{H>0\}\cap \{Y-Z> 0\}$.
Definition 4.9 A point where ![]() $\gamma _{s_1}$ or
$\gamma _{s_1}$ or ![]() $\zeta _{s_2}$ intersects
$\zeta _{s_2}$ intersects ![]() $\mathcal {E}\cap \{H > 0\}\cap \{Y-Z=0\}$ is called a
$\mathcal {E}\cap \{H > 0\}\cap \{Y-Z=0\}$ is called a ![]() $W$-intersection point.
$W$-intersection point.
We have the following proposition.
Proposition 4.10 Any ![]() $\gamma _{s_1}$ with
$\gamma _{s_1}$ with ![]() $s_1>-3$ (or
$s_1>-3$ (or ![]() $\zeta _{s_2}$ with
$\zeta _{s_2}$ with ![]() $s_2>0$) has a turning point at
$s_2>0$) has a turning point at ![]() $\mathcal {E}\cap \{H=0\}$ or a
$\mathcal {E}\cap \{H=0\}$ or a ![]() $W$-intersection point at
$W$-intersection point at ![]() $\mathcal {E}\cap \{Y-Z=0\}$.
$\mathcal {E}\cap \{Y-Z=0\}$.
Proof. An integral curve ![]() $\gamma _{s_1}$ with
$\gamma _{s_1}$ with ![]() $s_1>-3$ (or
$s_1>-3$ (or ![]() $\zeta _{s_2}$ with
$\zeta _{s_2}$ with ![]() $s_2>0$) is initially in the interior of the compact set
$s_2>0$) is initially in the interior of the compact set ![]() $\mathcal {E}\cap \{H\geq 0\}\cap \{Y-Z\geq 0\}$. Suppose the integral curve does not have any turning point or any
$\mathcal {E}\cap \{H\geq 0\}\cap \{Y-Z\geq 0\}$. Suppose the integral curve does not have any turning point or any ![]() $W$-intersection point. Then it must be defined on
$W$-intersection point. Then it must be defined on ![]() $\mathbb {R}$. Furthermore, such an integral curve is in
$\mathbb {R}$. Furthermore, such an integral curve is in ![]() $\mathcal {E}\cap \{H<1\}$ initially. From (2.11), along the integral curve we eventually have
$\mathcal {E}\cap \{H<1\}$ initially. From (2.11), along the integral curve we eventually have ![]() $H^2<1-\epsilon$ for some
$H^2<1-\epsilon$ for some ![]() $\epsilon >0$. Hence,
$\epsilon >0$. Hence,
eventually, meaning the function ![]() $H$ must at vanish some point. We reach a contradiction. Each integral curve without a turning point must have a
$H$ must at vanish some point. We reach a contradiction. Each integral curve without a turning point must have a ![]() $W$-intersection point.
$W$-intersection point.
We rephrase Lemma 4.4 in [Reference BöhmBöh98] with these new definitions.
Theorem 4.11 If ![]() $\gamma _{s_1}$ is not a heterocline for any
$\gamma _{s_1}$ is not a heterocline for any ![]() $s_1\in [a,b]$, then
$s_1\in [a,b]$, then ![]() $\sharp C(\gamma _{s_1})$ is a constant for all
$\sharp C(\gamma _{s_1})$ is a constant for all ![]() $s_1\in [a,b]$.
$s_1\in [a,b]$.
Immediately, we have the following proposition
Proposition 4.12 The quantities ![]() $\sharp C(\gamma _{0})$ and
$\sharp C(\gamma _{0})$ and ![]() $\sharp C(\zeta _{ {1}/({2m+6})})$ are both zero.
$\sharp C(\zeta _{ {1}/({2m+6})})$ are both zero.
Proof. From the defining equations of ![]() $\mathcal {B}_{QK}$, we have
$\mathcal {B}_{QK}$, we have ![]() $X_1=Y-2Z$ and
$X_1=Y-2Z$ and ![]() $X_2=-Z$ along
$X_2=-Z$ along ![]() $\gamma _{0}$. Then
$\gamma _{0}$. Then ![]() $H^2< 1$ becomes
$H^2< 1$ becomes ![]() $(3Y-(n+3)Z)^2< 1$. From (3.14) we have
$(3Y-(n+3)Z)^2< 1$. From (3.14) we have
 \begin{align} & \frac{12m}{n}(Y-Z)^2+6Y^2+4m(4m+8)YZ-12mZ^2> \frac{n-1}{n}(3Y-(4m+6)Z)^2 \nonumber\\ &\quad \Leftrightarrow n(n+9)(n-1)(Y-Z)Z> 0. \end{align}
\begin{align} & \frac{12m}{n}(Y-Z)^2+6Y^2+4m(4m+8)YZ-12mZ^2> \frac{n-1}{n}(3Y-(4m+6)Z)^2 \nonumber\\ &\quad \Leftrightarrow n(n+9)(n-1)(Y-Z)Z> 0. \end{align}
Hence, ![]() $X_1-X_2=Y-Z> 0$ along
$X_1-X_2=Y-Z> 0$ along ![]() $\gamma _0$. Similarly, we have
$\gamma _0$. Similarly, we have ![]() $X_2-X_1=Y-Z> 0$ along
$X_2-X_1=Y-Z> 0$ along ![]() $\zeta _{ {1}/({2m+6})}$. Note that
$\zeta _{ {1}/({2m+6})}$. Note that ![]() $X_1-X_2$ vanishes at the critical point
$X_1-X_2$ vanishes at the critical point ![]() $p_1^-$ and stays positive along
$p_1^-$ and stays positive along ![]() $\gamma _0$.
$\gamma _0$.
We are ready to prove Theorem 1.1.
Proof of Theorem 1.1 Consider a ![]() $\gamma _{s_1}$ with
$\gamma _{s_1}$ with ![]() $s_1\in ( {3}/({m-1}), {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)})$. From Lemma 4.7 we know that such a
$s_1\in ( {3}/({m-1}), {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)})$. From Lemma 4.7 we know that such a ![]() $\gamma _{s_1}$ is initially in
$\gamma _{s_1}$ is initially in ![]() $\mathcal {S}$. From (2.11) we know that such a
$\mathcal {S}$. From (2.11) we know that such a ![]() $\gamma _{s_1}$ must exit
$\gamma _{s_1}$ must exit ![]() $\mathcal {S}$. From Lemma 4.5 we know that such a
$\mathcal {S}$. From Lemma 4.5 we know that such a ![]() $\gamma _{s_1}$ exits
$\gamma _{s_1}$ exits ![]() $\mathcal {S}$ through the face
$\mathcal {S}$ through the face ![]() $\mathcal {E} \cap \{H> 0\}\cap \{Y-Z\geq 0\}\cap \{X_1-X_2=0\}$. It is clear that
$\mathcal {E} \cap \{H> 0\}\cap \{Y-Z\geq 0\}\cap \{X_1-X_2=0\}$. It is clear that ![]() $(\sqrt { {Z}/{Y}})'=\sqrt { {Z}/{Y}}(X_1-X_2)$. Since
$(\sqrt { {Z}/{Y}})'=\sqrt { {Z}/{Y}}(X_1-X_2)$. Since ![]() $Z$ is initially positive along
$Z$ is initially positive along ![]() $\gamma _{s_1}$ with
$\gamma _{s_1}$ with ![]() $s_1> {3}/({m-1})$, we know that
$s_1> {3}/({m-1})$, we know that ![]() $\sharp C(\gamma _{s_1})$ is exactly the number of times that
$\sharp C(\gamma _{s_1})$ is exactly the number of times that ![]() $\gamma _{s_1}$ intersects
$\gamma _{s_1}$ intersects ![]() $\mathcal {E} \cap \{H> 0\}\cap \{Y-Z\geq 0\}\cap \{X_1-X_2=0\}$. Hence,
$\mathcal {E} \cap \{H> 0\}\cap \{Y-Z\geq 0\}\cap \{X_1-X_2=0\}$. Hence, ![]() $\sharp C(\gamma _{s_1})\geq 1$ for
$\sharp C(\gamma _{s_1})\geq 1$ for ![]() $s_1\in ( {3}/({m-1}), {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)})$.
$s_1\in ( {3}/({m-1}), {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)})$.
On the other hand, the integral curve ![]() $\gamma _0$ joins
$\gamma _0$ joins ![]() $p_0^+$ and
$p_0^+$ and ![]() $p_1^-$. From Proposition 4.12, the function
$p_1^-$. From Proposition 4.12, the function ![]() $X_1-X_2$ stays positive along
$X_1-X_2$ stays positive along ![]() $\gamma _0$. Hence, we have
$\gamma _0$. Hence, we have ![]() $\sharp C(\gamma _0)=0$. Therefore, by Theorem 4.11 there exists some
$\sharp C(\gamma _0)=0$. Therefore, by Theorem 4.11 there exists some ![]() $s_\star \in (0, {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)})$ such that
$s_\star \in (0, {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)})$ such that ![]() $\gamma _{s_\star }$ is a heterocline that joins
$\gamma _{s_\star }$ is a heterocline that joins ![]() $p_0^\pm$. Theorem 1.1 is proved.
$p_0^\pm$. Theorem 1.1 is proved.
Remark 4.13 With some small modifications, the polynomial ![]() $\mathcal {S}$ can be applied to prove the existence of positive Einstein metrics on
$\mathcal {S}$ can be applied to prove the existence of positive Einstein metrics on ![]() $F^{m+1}$, a cohomogeneity-one space formed by the group triple
$F^{m+1}$, a cohomogeneity-one space formed by the group triple ![]() $(Sp(m)U(1),Sp(m)Sp(1),Sp(m+1))$. Furthermore, some non-existence results can also be obtained from the defining polynomial
$(Sp(m)U(1),Sp(m)Sp(1),Sp(m+1))$. Furthermore, some non-existence results can also be obtained from the defining polynomial ![]() $P$. For some cohomogeneity-one spaces, the function
$P$. For some cohomogeneity-one spaces, the function ![]() $P$ is negative along all
$P$ is negative along all ![]() $\gamma _{s_1}$ in
$\gamma _{s_1}$ in ![]() $\mathcal {E}\cap \{X_1-X_2\geq 0\}$, essentially forcing
$\mathcal {E}\cap \{X_1-X_2\geq 0\}$, essentially forcing ![]() $X_1-X_2$ to be positive along these integral curves. For example, there is no
$X_1-X_2$ to be positive along these integral curves. For example, there is no ![]() $\mathrm {Spin}(9)$-invariant cohomogeneity-one positive Einstein metric on
$\mathrm {Spin}(9)$-invariant cohomogeneity-one positive Einstein metric on ![]() $\mathbb {OP}^2\sharp \overline {\mathbb {OP}}^2$. A systematic study of the existence problem on all cohomogeneity-one spaces with two isotropy summands will be presented in later work.
$\mathbb {OP}^2\sharp \overline {\mathbb {OP}}^2$. A systematic study of the existence problem on all cohomogeneity-one spaces with two isotropy summands will be presented in later work.
Remark 4.14 One can recover Böhm's metric on ![]() $\mathbb {HP}^2\sharp \overline {\mathbb {HP}}^2$ by enlarging the set
$\mathbb {HP}^2\sharp \overline {\mathbb {HP}}^2$ by enlarging the set ![]() $\mathcal {S}$ for
$\mathcal {S}$ for ![]() $m=1$. Specifically, we can increase the coefficient for
$m=1$. Specifically, we can increase the coefficient for ![]() $Y$ in the polynomial
$Y$ in the polynomial ![]() $A$ properly so that, first, integral curves
$A$ properly so that, first, integral curves ![]() $\gamma _{s_1}$ with large enough
$\gamma _{s_1}$ with large enough ![]() $s_1$ are in the enlarged
$s_1$ are in the enlarged ![]() $\mathcal {S}$ initially; and second, integral curves that are in the enlarged
$\mathcal {S}$ initially; and second, integral curves that are in the enlarged ![]() $\mathcal {S}$ must exit through the face
$\mathcal {S}$ must exit through the face ![]() $\mathcal {S}\cap \{X_1-X_2=0\}$. Note that the derivative of the new polynomial
$\mathcal {S}\cap \{X_1-X_2=0\}$. Note that the derivative of the new polynomial ![]() $A$ still depends on the non-negativity of the same polynomial
$A$ still depends on the non-negativity of the same polynomial ![]() $P$. Hence,
$P$. Hence, ![]() $\sharp C(\gamma _{s_1})\geq 1$ with large enough
$\sharp C(\gamma _{s_1})\geq 1$ with large enough ![]() $s_1$ while
$s_1$ while ![]() $\sharp C(\gamma _{0})=0$, and Theorem 4.11 can be applied to prove the existence.
$\sharp C(\gamma _{0})=0$, and Theorem 4.11 can be applied to prove the existence.
We end this section with the following remark to discuss the motivation in defining ![]() $\mathcal {S}$.
$\mathcal {S}$.
Remark 4.15 Inspired by Corollary 5.8 in [Reference BöhmBöh98] and by the fact that ![]() $p_2^+$ is a stable node, we realized that taking the limit
$p_2^+$ is a stable node, we realized that taking the limit ![]() $s_1\to \infty$ for
$s_1\to \infty$ for ![]() $\gamma _{s_1}$ may not provide enough information to prove the existence theorem for all
$\gamma _{s_1}$ may not provide enough information to prove the existence theorem for all ![]() $m$. From (3.2) we know that
$m$. From (3.2) we know that ![]() $s_1$ is related to the initial condition
$s_1$ is related to the initial condition ![]() $f$. Numerical data in Table 2 in [Reference BöhmBöh98] indicate that the winding angle of
$f$. Numerical data in Table 2 in [Reference BöhmBöh98] indicate that the winding angle of ![]() $\gamma _{s_1}$ around
$\gamma _{s_1}$ around ![]() $\Phi$ may not be monotonic as
$\Phi$ may not be monotonic as ![]() $s_1$ increases. Hence, it is reasonable to find a bounded interval of
$s_1$ increases. Hence, it is reasonable to find a bounded interval of ![]() $s_1$ for which the winding angle of
$s_1$ for which the winding angle of ![]() $\gamma _{s_1}$ is large enough.
$\gamma _{s_1}$ is large enough.
From (4.19) and (4.24), it appears that the upper bound for ![]() $s_1$ can be easily controlled by changing the coefficient of
$s_1$ can be easily controlled by changing the coefficient of ![]() $YZ$ in
$YZ$ in ![]() $B$. Looking for an appropriate lower bound for
$B$. Looking for an appropriate lower bound for ![]() $s_1$, on the other hand, is relatively more difficult. Originally we choose to obtain the lower bound from
$s_1$, on the other hand, is relatively more difficult. Originally we choose to obtain the lower bound from ![]() $f_2\dot {f_2}\geq f_1\dot {f_1}$. The inequality is equivalent to
$f_2\dot {f_2}\geq f_1\dot {f_1}$. The inequality is equivalent to ![]() $YX_2\geq ZX_1$. Although the inequality is geometrically motivated, showing it can be maintained before the winding angle gets large enough seems to be too difficult. We eventually define the polynomial
$YX_2\geq ZX_1$. Although the inequality is geometrically motivated, showing it can be maintained before the winding angle gets large enough seems to be too difficult. We eventually define the polynomial ![]() $A$, whose first and second derivatives are relatively easier to control by polynomials
$A$, whose first and second derivatives are relatively easier to control by polynomials ![]() $P$ and
$P$ and ![]() $Q$.
$Q$.
5. Limiting winding angle
From [Reference WinkWin17] we know that ![]() $\gamma _\infty$ joins
$\gamma _\infty$ joins ![]() $p_0^+$ and
$p_0^+$ and ![]() $p_2^+$. By the symmetry of (2.7), we know that there exists
$p_2^+$. By the symmetry of (2.7), we know that there exists ![]() $\bar {\gamma }_\infty$ that joins
$\bar {\gamma }_\infty$ that joins ![]() $p_2^-$ and
$p_2^-$ and ![]() $p_0^-$. As
$p_0^-$. As ![]() $\Phi$ joins
$\Phi$ joins ![]() $p_2^\pm$, we have the set
$p_2^\pm$, we have the set ![]() $\{ \gamma _\infty, \Phi, \bar {\gamma }_\infty \}$ of heteroclines that joins
$\{ \gamma _\infty, \Phi, \bar {\gamma }_\infty \}$ of heteroclines that joins ![]() $p_0^\pm$. From this perspective, the critical point
$p_0^\pm$. From this perspective, the critical point ![]() $p_2^+$ is anticipated to play an important role in the qualitative analysis. Intuitively speaking, if
$p_2^+$ is anticipated to play an important role in the qualitative analysis. Intuitively speaking, if ![]() $p_2^+$ were a stable focus in the Ricci-flat subsystem, the integral curve
$p_2^+$ were a stable focus in the Ricci-flat subsystem, the integral curve ![]() $\gamma _{s_1}$ would wind around
$\gamma _{s_1}$ would wind around ![]() $\Phi$ more frequently as
$\Phi$ more frequently as ![]() $s_1$ increases. From § 3, however, we learn that
$s_1$ increases. From § 3, however, we learn that ![]() $p_2^+$ is a stable node in the Ricci-flat subsystem. Hence, the winding behavior of
$p_2^+$ is a stable node in the Ricci-flat subsystem. Hence, the winding behavior of ![]() $\gamma _{s_1}$ around
$\gamma _{s_1}$ around ![]() $\Phi$ is less obvious. The new coordinate change helps us estimate the limiting winding angle of
$\Phi$ is less obvious. The new coordinate change helps us estimate the limiting winding angle of ![]() $\gamma _{s_1}$ as
$\gamma _{s_1}$ as ![]() $s_1\to \infty$ and establish Theorem 1.2. On the other hand, another set
$s_1\to \infty$ and establish Theorem 1.2. On the other hand, another set ![]() $\{\zeta _\infty, \Phi, \bar {\zeta }_\infty \}$ of heteroclines joins
$\{\zeta _\infty, \Phi, \bar {\zeta }_\infty \}$ of heteroclines joins ![]() $p_1^\pm$. It is natural to ask if some heterocline other than
$p_1^\pm$. It is natural to ask if some heterocline other than ![]() $\zeta _0$ joins
$\zeta _0$ joins ![]() $p_1^\pm$. The new coordinate change also helps us to answer this question and prove Theorem 1.3.
$p_1^\pm$. The new coordinate change also helps us to answer this question and prove Theorem 1.3.
We introduce some known estimates in the Ricci-flat system in the following. The Ricci-flat subsystem on ![]() $\mathcal {E}\cap \{H=1\}$ is simply a subsystem of (2.16) in [Reference ChiChi21], with
$\mathcal {E}\cap \{H=1\}$ is simply a subsystem of (2.16) in [Reference ChiChi21], with ![]() $Y_1 \to \sqrt {2}$,
$Y_1 \to \sqrt {2}$, ![]() $Y_2\to \sqrt {2}Y$ and
$Y_2\to \sqrt {2}Y$ and ![]() $Y_3\to 2\sqrt {2}Z$. From Lemma 4.4 in [Reference ChiChi21], we learn that the compact set
$Y_3\to 2\sqrt {2}Z$. From Lemma 4.4 in [Reference ChiChi21], we learn that the compact set
is invariant. Critical points ![]() $p_0^+$ and
$p_0^+$ and ![]() $p_1^+$ are on the boundary of
$p_1^+$ are on the boundary of ![]() $\hat {\mathcal {B}}_{{\rm RF}}$ while
$\hat {\mathcal {B}}_{{\rm RF}}$ while ![]() $p_2^+$ is in the interior. Straightforward computations show that
$p_2^+$ is in the interior. Straightforward computations show that ![]() $\gamma _\infty$ and
$\gamma _\infty$ and ![]() $\zeta _\infty$ are initially in
$\zeta _\infty$ are initially in ![]() $\hat {\mathcal {B}}_{{\rm RF}}$. From Lemma 5.7 in [Reference ChiChi21], it is known that these two integral curves converge to
$\hat {\mathcal {B}}_{{\rm RF}}$. From Lemma 5.7 in [Reference ChiChi21], it is known that these two integral curves converge to ![]() $p_2^+$. We construct the following invariant set introduced in [Reference ChiChi19], which gives us more information on
$p_2^+$. We construct the following invariant set introduced in [Reference ChiChi19], which gives us more information on ![]() $\gamma _\infty$ near
$\gamma _\infty$ near ![]() $p_2^+$.
$p_2^+$.
Proposition 5.1 The set
is compact and invariant.
Proof. The compactness is derived from ![]() $Y-(2m+3)Z\geq 0$ and (2.9).
$Y-(2m+3)Z\geq 0$ and (2.9).
Since
 \begin{align} & \langle\nabla(Y-(2m+3)Z),V\rangle_{\mathcal{B}_{RF}\cap \{Y-(2m+3)Z=0\}} \nonumber\\ &\quad =(Y-(2m+3)Z)\left(H\left(G+\frac{1}{n}(1-H^2)\right)-X_1-(4m+6)Z\right) \nonumber\\ &\qquad +(4m+6)Z(X_2-X_1+Y-(2m+3)Z) \nonumber\\ &\quad =(4m+6)Z(X_2-X_1+Y-(2m+3)Z)\quad \text{since $Y-(2m+3)Z=0$} \nonumber\\ &\quad \geq 0, \end{align}
\begin{align} & \langle\nabla(Y-(2m+3)Z),V\rangle_{\mathcal{B}_{RF}\cap \{Y-(2m+3)Z=0\}} \nonumber\\ &\quad =(Y-(2m+3)Z)\left(H\left(G+\frac{1}{n}(1-H^2)\right)-X_1-(4m+6)Z\right) \nonumber\\ &\qquad +(4m+6)Z(X_2-X_1+Y-(2m+3)Z) \nonumber\\ &\quad =(4m+6)Z(X_2-X_1+Y-(2m+3)Z)\quad \text{since $Y-(2m+3)Z=0$} \nonumber\\ &\quad \geq 0, \end{align}
the vector field ![]() $V$ points inward on the boundary
$V$ points inward on the boundary ![]() $\mathcal {B}_{{\rm RF}}\cap \{Y-(2m+3)Z=0\}$. As for
$\mathcal {B}_{{\rm RF}}\cap \{Y-(2m+3)Z=0\}$. As for ![]() $\mathcal {B}_{{\rm RF}}\cap \{X_2-X_1+Y-(2m+3)Z=0\}$, from (2.9) we have
$\mathcal {B}_{{\rm RF}}\cap \{X_2-X_1+Y-(2m+3)Z=0\}$, from (2.9) we have
 \begin{align} & \frac{12m}{n}(Y-(2m+3)Z)^2+6Y^2+4m(4m+8)YZ-12mZ^2=\frac{n-1}{n} \nonumber\\ &\quad \Leftrightarrow 18(2m+1)Y^2+8m(8m^2+16m+3)YZ+24m(2m^2+4m+3)Z^2=4m+2. \end{align}
\begin{align} & \frac{12m}{n}(Y-(2m+3)Z)^2+6Y^2+4m(4m+8)YZ-12mZ^2=\frac{n-1}{n} \nonumber\\ &\quad \Leftrightarrow 18(2m+1)Y^2+8m(8m^2+16m+3)YZ+24m(2m^2+4m+3)Z^2=4m+2. \end{align}Then we have
 \begin{align} &
\langle\nabla(X_2-X_1+Y-(2m+3)Z),V\rangle_{\mathcal{B}_{{\rm
RF}}\cap \{X_2-X_1+Y-(2m+3)Z)=0\}} \nonumber\\ &\quad
=(X_2-X_1+Y-(2m+3)Z))\left(H\left(G+\frac{1}{n}(1-H^2)-1\right)+
\frac{4m}{n}Y+\frac{8m^2+24m+18}{n}Z\right) \nonumber\\
&\qquad
+\frac{1}{n}(Y-(2m+3)Z)((4m+2)H-(12m+6)Y-(8m^2+16m+12)Z)
\nonumber\\ &\quad
=\frac{1}{n}(Y-(2m+3)Z)(4m+2-(12m+6)Y-(8m^2+16m+12)Z)
\nonumber\\ &\text{since $H=1$ and $X_2-X_1+Y-(2m+3)Z=0$}.
\end{align}
\begin{align} &
\langle\nabla(X_2-X_1+Y-(2m+3)Z),V\rangle_{\mathcal{B}_{{\rm
RF}}\cap \{X_2-X_1+Y-(2m+3)Z)=0\}} \nonumber\\ &\quad
=(X_2-X_1+Y-(2m+3)Z))\left(H\left(G+\frac{1}{n}(1-H^2)-1\right)+
\frac{4m}{n}Y+\frac{8m^2+24m+18}{n}Z\right) \nonumber\\
&\qquad
+\frac{1}{n}(Y-(2m+3)Z)((4m+2)H-(12m+6)Y-(8m^2+16m+12)Z)
\nonumber\\ &\quad
=\frac{1}{n}(Y-(2m+3)Z)(4m+2-(12m+6)Y-(8m^2+16m+12)Z)
\nonumber\\ &\text{since $H=1$ and $X_2-X_1+Y-(2m+3)Z=0$}.
\end{align}
With ![]() $Y,Z\geq 0$, showing
$Y,Z\geq 0$, showing ![]() $4m+2-(12m+6)Y-(8m^2+16m+12)Z\geq 0$ is equivalent to showing
$4m+2-(12m+6)Y-(8m^2+16m+12)Z\geq 0$ is equivalent to showing ![]() $(4m+2)^2\geq ((12m+6)Y+(8m^2+16m+12)Z)^2$. Note that
$(4m+2)^2\geq ((12m+6)Y+(8m^2+16m+12)Z)^2$. Note that ![]() $(4m+2)^2$ is simply the left-hand side of (5.2) multiplied by
$(4m+2)^2$ is simply the left-hand side of (5.2) multiplied by ![]() $4m+2$. Hence, one can obtain the non-negativity by verifying
$4m+2$. Hence, one can obtain the non-negativity by verifying
 \begin{align} & (4m+2)(18(2m+1)Y^2+8m(8m^2+16m+3)YZ+24m(2m^2+4m+3)Z^2) \nonumber\\ &\quad \geq ((12m+6)Y+(8m^2+16m+12)Z)^2 \nonumber\\ &\quad \Leftrightarrow 16 n(m-1)((4m^2+8m+3) YZ + (2m^2+ 4m+3)Z^2)\geq 0. \end{align}
\begin{align} & (4m+2)(18(2m+1)Y^2+8m(8m^2+16m+3)YZ+24m(2m^2+4m+3)Z^2) \nonumber\\ &\quad \geq ((12m+6)Y+(8m^2+16m+12)Z)^2 \nonumber\\ &\quad \Leftrightarrow 16 n(m-1)((4m^2+8m+3) YZ + (2m^2+ 4m+3)Z^2)\geq 0. \end{align}
Note that the equality is obtained for ![]() $m=1$. Hence, (5.3) is non-negative and identically vanishes if
$m=1$. Hence, (5.3) is non-negative and identically vanishes if ![]() $m=1$. Hence,
$m=1$. Hence, ![]() $\mathcal {B}_{{\rm RF}}$ is invariant.
$\mathcal {B}_{{\rm RF}}$ is invariant.
Remark 5.2 With (2.9) one can easily show that
Therefore, the fact that (5.3) identically vanishes for ![]() $m=1$ recovers the invariant set
$m=1$ recovers the invariant set ![]() $\mathcal {B}_{\mathrm {Spin}(7)}$ as in (3.4).
$\mathcal {B}_{\mathrm {Spin}(7)}$ as in (3.4).
Remark 5.3 By (5.1) and (5.3), one can also show that the set
is also invariant. Furthermore, we have the following proposition.
Proposition 5.4 For ![]() $m\geq 2$, the integral curve
$m\geq 2$, the integral curve ![]() $\gamma _\infty$ is in
$\gamma _\infty$ is in ![]() $\mathcal {B}_{{\rm RF}}$ initially. For
$\mathcal {B}_{{\rm RF}}$ initially. For ![]() $m=1$, the integral curve
$m=1$, the integral curve ![]() $\gamma _\infty$ stays on the boundary of
$\gamma _\infty$ stays on the boundary of ![]() $\mathcal {B}_{{\rm RF}}$. For
$\mathcal {B}_{{\rm RF}}$. For ![]() $m\geq 1$, the integral curve
$m\geq 1$, the integral curve ![]() $\zeta _\infty$ is in
$\zeta _\infty$ is in ![]() $\tilde {\mathcal {B}}_{{\rm RF}}$ initially.
$\tilde {\mathcal {B}}_{{\rm RF}}$ initially.
Proof. The statement is clear by (3.3) and (3.13). Note that for ![]() $m=1$, the function
$m=1$, the function ![]() $X_2-X_1+Y-5Z$ is identically zero on
$X_2-X_1+Y-5Z$ is identically zero on ![]() $\gamma _\infty$.
$\gamma _\infty$.
To obtain more information on how ![]() $\gamma _{s_1}$ and
$\gamma _{s_1}$ and ![]() $\zeta _{s_2}$ wind around
$\zeta _{s_2}$ wind around ![]() $\Phi$ as
$\Phi$ as ![]() $s_1,s_2\to \infty$, we consider the ‘cylindrical’ coordinates
$s_1,s_2\to \infty$, we consider the ‘cylindrical’ coordinates
The system (2.7) is transformed into
 \begin{align} \begin{bmatrix}
H\\ r\\
\theta\\ Y \end{bmatrix}'\,{=}\begin{bmatrix}
(H^2-1)\left(\dfrac{1}{n}+\dfrac{12m}{n}
r^2\sin^2(\theta)\right)\\
rH\left(\dfrac{1}{n}+\dfrac{12m}{n}r^2\sin^2(\theta)\right)\,{-}\,Hr\sin^2(\theta)\,{-}\,
\dfrac{H}{n}r\cos^2(\theta)\,{+}\,\left(\dfrac{m+2}{m+1}\,{+}\,\dfrac{3}{n}\right)r^2\sin(\theta)\cos^2(\theta)\\
2\sqrt{\dfrac{2m+2}{2m+3}}Y\,{+}\,\dfrac{1}{m+1}r\cos(\theta)\,{-}\,\dfrac{n-1}{n}H\sin(\theta)\cos(\theta)\,{-}\,
\left(\dfrac{m+2}{m+1}+\dfrac{3}{n}\right)r\cos(\theta)\sin^2(\theta)\\
Y\left(\dfrac{12m}{n} H
r^2\sin^2(\theta)-\dfrac{4m}{n}r\sin(\theta)\right)
\end{bmatrix} \end{align}
\begin{align} \begin{bmatrix}
H\\ r\\
\theta\\ Y \end{bmatrix}'\,{=}\begin{bmatrix}
(H^2-1)\left(\dfrac{1}{n}+\dfrac{12m}{n}
r^2\sin^2(\theta)\right)\\
rH\left(\dfrac{1}{n}+\dfrac{12m}{n}r^2\sin^2(\theta)\right)\,{-}\,Hr\sin^2(\theta)\,{-}\,
\dfrac{H}{n}r\cos^2(\theta)\,{+}\,\left(\dfrac{m+2}{m+1}\,{+}\,\dfrac{3}{n}\right)r^2\sin(\theta)\cos^2(\theta)\\
2\sqrt{\dfrac{2m+2}{2m+3}}Y\,{+}\,\dfrac{1}{m+1}r\cos(\theta)\,{-}\,\dfrac{n-1}{n}H\sin(\theta)\cos(\theta)\,{-}\,
\left(\dfrac{m+2}{m+1}+\dfrac{3}{n}\right)r\cos(\theta)\sin^2(\theta)\\
Y\left(\dfrac{12m}{n} H
r^2\sin^2(\theta)-\dfrac{4m}{n}r\sin(\theta)\right)
\end{bmatrix} \end{align}
with conservation law (2.9) rewritten as
 \begin{gather*} C_{\Lambda\geq 0}\colon \frac{12m}{n}r^2\sin^2(\theta)+6Y^2+4m(4m+8)Y\tilde{Z}-12m\tilde{Z}^2=1-\frac{1}{n},\\ \tilde{Z}=\left(\frac{Y}{2m+3}-\frac{r\cos(\theta)}{\sqrt{(2m+2)(2m+3)}}\right). \end{gather*}
\begin{gather*} C_{\Lambda\geq 0}\colon \frac{12m}{n}r^2\sin^2(\theta)+6Y^2+4m(4m+8)Y\tilde{Z}-12m\tilde{Z}^2=1-\frac{1}{n},\\ \tilde{Z}=\left(\frac{Y}{2m+3}-\frac{r\cos(\theta)}{\sqrt{(2m+2)(2m+3)}}\right). \end{gather*}
The set ![]() $\mathcal {E}$ is then defined in the
$\mathcal {E}$ is then defined in the ![]() $(H,r,\theta,Y)$-coordinate accordingly. The variable
$(H,r,\theta,Y)$-coordinate accordingly. The variable ![]() $r$ tells us the distance from a point to
$r$ tells us the distance from a point to ![]() $\Phi$ and
$\Phi$ and ![]() $\theta$ records the winding angle around
$\theta$ records the winding angle around ![]() $\Phi$.
$\Phi$.
With the new conservation law, setting ![]() $r=0$ implies
$r=0$ implies ![]() $Y=(2m+3)z_0$. Restricting (5.6) to the invariant set
$Y=(2m+3)z_0$. Restricting (5.6) to the invariant set ![]() $\mathcal {E}\cap \{r=0\}$ gives the subsystem
$\mathcal {E}\cap \{r=0\}$ gives the subsystem
 \begin{equation} \begin{bmatrix} H\\ \theta \end{bmatrix}'=\begin{bmatrix} (H^2-1)\dfrac{1}{n}\\ 2\sqrt{(2m+2)(2m+3)}z_0-\dfrac{n-1}{n}H\sin(\theta)\cos(\theta) \end{bmatrix},\quad r=0,\quad Y=(2m+3)z_0. \end{equation}
\begin{equation} \begin{bmatrix} H\\ \theta \end{bmatrix}'=\begin{bmatrix} (H^2-1)\dfrac{1}{n}\\ 2\sqrt{(2m+2)(2m+3)}z_0-\dfrac{n-1}{n}H\sin(\theta)\cos(\theta) \end{bmatrix},\quad r=0,\quad Y=(2m+3)z_0. \end{equation}
This subsystem is essentially the integral curve ![]() $\Phi$. Straightforward computations show that (5.6) has the following four sequences of critical points in
$\Phi$. Straightforward computations show that (5.6) has the following four sequences of critical points in ![]() $\mathcal {E}\cap \{r=0\}$:
$\mathcal {E}\cap \{r=0\}$:
 \begin{align} \begin{aligned} \{A_i^\pm:=(\pm 1,0,a_i^\pm,(2m+3)z_0)\}_{i\in\mathbb{Z}},\quad a_i^\pm=\pm\arctan\left(-\frac{\delta_1}{2\sqrt{(2m+3)(2m+2)}z_0}\right)+i\pi,\\ \{B_i^\pm:=(\pm 1,0,b_i^\pm,(2m+3)z_0)\}_{i\in\mathbb{Z}},\quad b_i^\pm=\pm\arctan\left(-\frac{\delta_2}{2\sqrt{(2m+3)(2m+2)}z_0}\right)+i\pi. \end{aligned} \end{align}
\begin{align} \begin{aligned} \{A_i^\pm:=(\pm 1,0,a_i^\pm,(2m+3)z_0)\}_{i\in\mathbb{Z}},\quad a_i^\pm=\pm\arctan\left(-\frac{\delta_1}{2\sqrt{(2m+3)(2m+2)}z_0}\right)+i\pi,\\ \{B_i^\pm:=(\pm 1,0,b_i^\pm,(2m+3)z_0)\}_{i\in\mathbb{Z}},\quad b_i^\pm=\pm\arctan\left(-\frac{\delta_2}{2\sqrt{(2m+3)(2m+2)}z_0}\right)+i\pi. \end{aligned} \end{align}
Furthermore, for each ![]() $i\in \mathbb {Z}$ we have
$i\in \mathbb {Z}$ we have
 \begin{equation} \begin{gathered}
a_i^+\in \left(i\pi,\frac{\pi}{4}+i\pi\right),\quad
b_i^+\in\left(\frac{\pi}{4}+i\pi,\frac{\pi}{2}+i\pi\right),\\
b_i^-\in
\left(-\frac{\pi}{2}+i\pi,-\frac{\pi}{4}+i\pi\right),\quad
a_i^-\in \left(-\frac{\pi}{4}+i\pi,i\pi\right).
\end{gathered}
\end{equation}
\begin{equation} \begin{gathered}
a_i^+\in \left(i\pi,\frac{\pi}{4}+i\pi\right),\quad
b_i^+\in\left(\frac{\pi}{4}+i\pi,\frac{\pi}{2}+i\pi\right),\\
b_i^-\in
\left(-\frac{\pi}{2}+i\pi,-\frac{\pi}{4}+i\pi\right),\quad
a_i^-\in \left(-\frac{\pi}{4}+i\pi,i\pi\right).
\end{gathered}
\end{equation}Remark 5.5 Computations show that ![]() $A_i^+$ and
$A_i^+$ and ![]() $B_i^+$ are transformed respectively from the two stable eigenvectors
$B_i^+$ are transformed respectively from the two stable eigenvectors ![]() $u_1$ and
$u_1$ and ![]() $u_2$ of the linearization at
$u_2$ of the linearization at ![]() $p_2^+$. Recall from § 3 that both
$p_2^+$. Recall from § 3 that both ![]() $u_1$ and
$u_1$ and ![]() $u_2$ are tangent to
$u_2$ are tangent to ![]() $\mathcal {E}\cap \{H=1\}$, and the corresponding eigenvalues
$\mathcal {E}\cap \{H=1\}$, and the corresponding eigenvalues ![]() $\delta _1$ and
$\delta _1$ and ![]() $\delta _2$ are real numbers and we have
$\delta _2$ are real numbers and we have ![]() $\delta _2<\delta _1<0$. Each linearized solution to the Ricci-flat subsystem around
$\delta _2<\delta _1<0$. Each linearized solution to the Ricci-flat subsystem around ![]() $p_2^+$ must have
$p_2^+$ must have ![]() $e^{\delta _2\eta }\ll e^{\delta _1\eta }$ as
$e^{\delta _2\eta }\ll e^{\delta _1\eta }$ as ![]() $\eta \to \infty$. Hence, integral curves
$\eta \to \infty$. Hence, integral curves ![]() $\gamma _\infty$ and
$\gamma _\infty$ and ![]() $\zeta _\infty$ converge to
$\zeta _\infty$ converge to ![]() $p_2^+$ along
$p_2^+$ along ![]() $u_1$. Hence, it is not surprising that
$u_1$. Hence, it is not surprising that ![]() $A_i^+$ are sinks and
$A_i^+$ are sinks and ![]() $B_i^+$ are saddles in the subsystem of (5.6) restricted to
$B_i^+$ are saddles in the subsystem of (5.6) restricted to ![]() $\mathcal {E}\cap \{H=1\}$. Furthermore, for the subsystem (5.7), critical points
$\mathcal {E}\cap \{H=1\}$. Furthermore, for the subsystem (5.7), critical points ![]() $A_i^+$ are saddles, and
$A_i^+$ are saddles, and ![]() $B_i^+$ are sources.
$B_i^+$ are sources.
Thanks to the invariant set ![]() $\mathcal {B}_{{\rm RF}}$ in Proposition 5.1, whose boundary contains
$\mathcal {B}_{{\rm RF}}$ in Proposition 5.1, whose boundary contains ![]() $p_2^+$, we are now ready to show that both
$p_2^+$, we are now ready to show that both ![]() $\gamma _\infty$ and
$\gamma _\infty$ and ![]() $\zeta _\infty$ do not wind fully around
$\zeta _\infty$ do not wind fully around ![]() $p_2^+$.
$p_2^+$.
Proposition 5.6 Consider the ![]() $(H,r,\theta,Y)$-coordinate. For
$(H,r,\theta,Y)$-coordinate. For ![]() $m\geq 2$, the integral curve
$m\geq 2$, the integral curve ![]() $\gamma _\infty$ joins the critical points
$\gamma _\infty$ joins the critical points ![]() $p_0^+$ and
$p_0^+$ and ![]() $A_0^+$. For
$A_0^+$. For ![]() $m=1$, the variable
$m=1$, the variable ![]() $\theta$ remains a constant along
$\theta$ remains a constant along ![]() $\gamma _\infty$ and the integral curve joins
$\gamma _\infty$ and the integral curve joins ![]() $p_0^+$ and
$p_0^+$ and ![]() $B_0^+$. For
$B_0^+$. For ![]() $m\geq 1$, the integral curve
$m\geq 1$, the integral curve ![]() $\zeta _\infty$ joins the critical points
$\zeta _\infty$ joins the critical points ![]() $p_1^+$ and
$p_1^+$ and ![]() $A_1^+$.
$A_1^+$.
Proof. In the new coordinate, the critical point ![]() $p_0^+$ is
$p_0^+$ is
 \[\left(1,\frac{1}{3}\sqrt{\frac{4m+5}{2m+3}},\arctan\left(\sqrt{\frac{2m+3}{2m+2}}\right),\frac{1}{3}\right).\]
\[\left(1,\frac{1}{3}\sqrt{\frac{4m+5}{2m+3}},\arctan\left(\sqrt{\frac{2m+3}{2m+2}}\right),\frac{1}{3}\right).\]
As ![]() $\gamma _\infty$ joins
$\gamma _\infty$ joins ![]() $p_0^+$ and
$p_0^+$ and ![]() $p_2^+$ in the
$p_2^+$ in the ![]() $(X_1,X_2,Y,Z)$-coordinate, it is clear that the integral curve joins
$(X_1,X_2,Y,Z)$-coordinate, it is clear that the integral curve joins ![]() $p_0^+$ and one of
$p_0^+$ and one of ![]() $A_i^+$ or
$A_i^+$ or ![]() $B_i^+$ in the new coordinate. From Propositions 5.1 and 5.4 we know that
$B_i^+$ in the new coordinate. From Propositions 5.1 and 5.4 we know that ![]() $r\cos (\theta )\geq 0$ and
$r\cos (\theta )\geq 0$ and ![]() $\sqrt { ({2m+3})/({2m+2})}r\cos (\theta )-r\sin (\theta )\geq 0$ along
$\sqrt { ({2m+3})/({2m+2})}r\cos (\theta )-r\sin (\theta )\geq 0$ along ![]() $\gamma _\infty$. In particular, the second inequality reaches equality so that
$\gamma _\infty$. In particular, the second inequality reaches equality so that ![]() $\theta =\arctan (\sqrt { ({2m+3})/({2m+2})})$ along
$\theta =\arctan (\sqrt { ({2m+3})/({2m+2})})$ along ![]() $\gamma _\infty$ for
$\gamma _\infty$ for ![]() $m=1$. Note that
$m=1$. Note that ![]() $0< a_0^+<\arctan (\sqrt { ({2m+3})/({2m+2})})\leq b_0^+$ and the last inequality reaches equality only for
$0< a_0^+<\arctan (\sqrt { ({2m+3})/({2m+2})})\leq b_0^+$ and the last inequality reaches equality only for ![]() $m=1$. The
$m=1$. The ![]() $\theta$-coordinate for
$\theta$-coordinate for ![]() $p_0^+$ is positive and
$p_0^+$ is positive and ![]() $\{\theta \geq 0\}$ is clearly invariant. Hence, for
$\{\theta \geq 0\}$ is clearly invariant. Hence, for ![]() $m\geq 2$, the integral curve
$m\geq 2$, the integral curve ![]() $\gamma _\infty$ converges to
$\gamma _\infty$ converges to ![]() $A_0^+$; for
$A_0^+$; for ![]() $m=1$, the integral curve
$m=1$, the integral curve ![]() $\gamma _\infty$ converges to
$\gamma _\infty$ converges to ![]() $B_0^+$ as
$B_0^+$ as ![]() $\theta =b_0^+$ along
$\theta =b_0^+$ along ![]() $\gamma _\infty$.
$\gamma _\infty$.
In the ![]() $(H,r,\theta,Y)$-coordinate, the critical point
$(H,r,\theta,Y)$-coordinate, the critical point ![]() $p_1^+$ is
$p_1^+$ is
 \[\left(1,\sqrt{\frac{2m+2}{2m+3}}\frac{2m+2}{n},\pi,\frac{1}{n}\right).\]
\[\left(1,\sqrt{\frac{2m+2}{2m+3}}\frac{2m+2}{n},\pi,\frac{1}{n}\right).\]
It is established in [Reference ChiChi21] that ![]() $\zeta _\infty$ is an integral curve that joins
$\zeta _\infty$ is an integral curve that joins ![]() $p_1^+$ and
$p_1^+$ and ![]() $p_2^+$ in the
$p_2^+$ in the ![]() $(X_1,X_2,Y,Z)$-coordinate. Therefore, in the
$(X_1,X_2,Y,Z)$-coordinate. Therefore, in the ![]() $(H,r,\theta,Y)$-coordinate, the integral curve
$(H,r,\theta,Y)$-coordinate, the integral curve ![]() $\zeta _\infty$ joins
$\zeta _\infty$ joins ![]() $p_1^+$ and one of
$p_1^+$ and one of ![]() $A_i^+$ or
$A_i^+$ or ![]() $B_i^+$. As
$B_i^+$. As ![]() $\zeta _\infty$ is in
$\zeta _\infty$ is in ![]() $\tilde {\mathcal {B}}_{{\rm RF}}$ initially, by Remark 5.3 we know that
$\tilde {\mathcal {B}}_{{\rm RF}}$ initially, by Remark 5.3 we know that ![]() $\cos (\theta )=\sqrt { ({2m+2})/({2m+3})}(Y-(2m+3)Z)\leq 0$ and
$\cos (\theta )=\sqrt { ({2m+2})/({2m+3})}(Y-(2m+3)Z)\leq 0$ and ![]() $\sqrt { ({2m+3})/({2m+2})}r\cos (\theta )-r\sin (\theta )\leq 0$ along
$\sqrt { ({2m+3})/({2m+2})}r\cos (\theta )-r\sin (\theta )\leq 0$ along ![]() $\zeta _\infty$. Hence, we know that
$\zeta _\infty$. Hence, we know that ![]() $ {\pi }/{2}\leq \theta \leq \arctan (\sqrt { ({2m+3})/({2m+2})})+\pi \leq b_1^+$ along
$ {\pi }/{2}\leq \theta \leq \arctan (\sqrt { ({2m+3})/({2m+2})})+\pi \leq b_1^+$ along ![]() $\zeta _\infty$. Therefore,
$\zeta _\infty$. Therefore, ![]() $\zeta _\infty$ converges to
$\zeta _\infty$ converges to ![]() $A_1^+$ for
$A_1^+$ for ![]() $m\geq 2$. We claim that the integral curve
$m\geq 2$. We claim that the integral curve ![]() $\zeta _\infty$ also converges to
$\zeta _\infty$ also converges to ![]() $A_1^+$ for
$A_1^+$ for ![]() $m=1$. Recall Remarks 4.3 and 5.2. The integral curve
$m=1$. Recall Remarks 4.3 and 5.2. The integral curve ![]() $\chi$ also converges to
$\chi$ also converges to ![]() $p_2^+$ and along
$p_2^+$ and along ![]() $\chi$ we have
$\chi$ we have ![]() $X_2-X_1\geq 0$ and
$X_2-X_1\geq 0$ and ![]() $X_2-X_1+Y-5Z=0$. Hence,
$X_2-X_1+Y-5Z=0$. Hence, ![]() $\chi$ converges to
$\chi$ converges to ![]() $B_1^+$ in the
$B_1^+$ in the ![]() $(H,r,\theta,Y)$-coordinate. As the linearization at
$(H,r,\theta,Y)$-coordinate. As the linearization at ![]() $B_1^+$ has only one stable eigenvector, we know that
$B_1^+$ has only one stable eigenvector, we know that ![]() $\zeta _\infty$ converges to
$\zeta _\infty$ converges to ![]() $A_1^+$.
$A_1^+$.
We claim the following lemma.
Lemma 5.7 Let ![]() $\Pi$ be the integral curve of the subsystem (5.7) that emanates from
$\Pi$ be the integral curve of the subsystem (5.7) that emanates from ![]() $A_0^+$. Let
$A_0^+$. Let ![]() $(0,0,\theta _*,(2m+3)z_0)$ be the midpoint of
$(0,0,\theta _*,(2m+3)z_0)$ be the midpoint of ![]() $\Pi$ at which it passes through
$\Pi$ at which it passes through ![]() $H=0$. For
$H=0$. For ![]() $m\geq 2$, we have
$m\geq 2$, we have ![]() $\theta _*=\lim _{s_1\to \infty }\theta (\gamma _{s_1}\cap \{H=0\})$.
$\theta _*=\lim _{s_1\to \infty }\theta (\gamma _{s_1}\cap \{H=0\})$.
Proof. We think of (5.6) on ![]() $\mathcal {E}$ as a dynamical system in the three-dimensional
$\mathcal {E}$ as a dynamical system in the three-dimensional ![]() $Hr\theta$-space with
$Hr\theta$-space with ![]() $Y$ as a function in
$Y$ as a function in ![]() $(H,r,\theta )$. As mentioned in Remark 5.5, each
$(H,r,\theta )$. As mentioned in Remark 5.5, each ![]() $A_i^+$ is a saddle whose linearization has two stable eigenvectors and one unstable eigenvector. Furthermore, the two stable eigenvectors are parallel to
$A_i^+$ is a saddle whose linearization has two stable eigenvectors and one unstable eigenvector. Furthermore, the two stable eigenvectors are parallel to ![]() $\mathcal {E}\cap \{H=1\}$, meaning that each
$\mathcal {E}\cap \{H=1\}$, meaning that each ![]() $A_i^+$ is a sink in the Ricci-flat subsystem and
$A_i^+$ is a sink in the Ricci-flat subsystem and ![]() $\Pi$ is the only integral curve that emanates from
$\Pi$ is the only integral curve that emanates from ![]() $A_i^+$ in
$A_i^+$ in ![]() $\mathcal {E}\cap \{H<1\}$. By the Hartman–Grobman theorem, there is a local homeomorphism
$\mathcal {E}\cap \{H<1\}$. By the Hartman–Grobman theorem, there is a local homeomorphism ![]() $(\phi, \mathcal {U})$ defined around
$(\phi, \mathcal {U})$ defined around ![]() $A_0^+$ through which the system (5.6) is topologically equivalent to the linear dynamical system
$A_0^+$ through which the system (5.6) is topologically equivalent to the linear dynamical system
 \begin{equation} \begin{bmatrix} x\\ y\\ z \end{bmatrix}'=\begin{bmatrix} -1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & 1\\ \end{bmatrix}\begin{bmatrix} x\\ y\\ z \end{bmatrix}. \end{equation}
\begin{equation} \begin{bmatrix} x\\ y\\ z \end{bmatrix}'=\begin{bmatrix} -1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & 1\\ \end{bmatrix}\begin{bmatrix} x\\ y\\ z \end{bmatrix}. \end{equation}In particular, we have
Let ![]() $D_\epsilon$ be an open disk on the
$D_\epsilon$ be an open disk on the ![]() $xy$-plane with radius
$xy$-plane with radius ![]() $\epsilon _1$. Let
$\epsilon _1$. Let ![]() $U_1$ be the cylinder
$U_1$ be the cylinder ![]() $D_{\epsilon _1}\times (-\epsilon _2,\epsilon _2]$. Note that integral curves in
$D_{\epsilon _1}\times (-\epsilon _2,\epsilon _2]$. Note that integral curves in ![]() $U_1\cap \{z>0\}$ can only escape through the face
$U_1\cap \{z>0\}$ can only escape through the face ![]() $D_{\epsilon _1}\times \{\epsilon _2\}$. Choose small enough
$D_{\epsilon _1}\times \{\epsilon _2\}$. Choose small enough ![]() $\epsilon _1$ and
$\epsilon _1$ and ![]() $\epsilon _2$ so that
$\epsilon _2$ so that ![]() $\mathcal {U}_1:=\phi ^{-1}(U_1)$ is contained in
$\mathcal {U}_1:=\phi ^{-1}(U_1)$ is contained in ![]() $\mathcal {U}$. Then
$\mathcal {U}$. Then ![]() $p:=\phi ^{-1}(0,0,\epsilon _2)$ is a point on
$p:=\phi ^{-1}(0,0,\epsilon _2)$ is a point on ![]() $\mathcal {U}\cap \Pi$.
$\mathcal {U}\cap \Pi$.
Let ![]() $\mathcal {U}_0$ be an open neighborhood around the point
$\mathcal {U}_0$ be an open neighborhood around the point ![]() $(0,0,\theta _*)$ in the
$(0,0,\theta _*)$ in the ![]() $Hr\theta$-space. By the continuous dependence, there exists an open set
$Hr\theta$-space. By the continuous dependence, there exists an open set ![]() $\mathcal {U}_2\ni p$ in
$\mathcal {U}_2\ni p$ in ![]() $\mathcal {U}$ such that any point in
$\mathcal {U}$ such that any point in ![]() $\mathcal {U}_2$ lies on an integral curve that enters
$\mathcal {U}_2$ lies on an integral curve that enters ![]() $\mathcal {U}_0$. It is clear that
$\mathcal {U}_0$. It is clear that ![]() $p\in \mathcal {U}_1\cap \mathcal {U}_2$. Modify
$p\in \mathcal {U}_1\cap \mathcal {U}_2$. Modify ![]() $U_1$ by shrinking
$U_1$ by shrinking ![]() $\epsilon _1$ so that
$\epsilon _1$ so that ![]() $D_{\epsilon _1}\times \{\epsilon _2\}$ is contained in
$D_{\epsilon _1}\times \{\epsilon _2\}$ is contained in ![]() $\phi (\mathcal {U}_2)$ while leaving
$\phi (\mathcal {U}_2)$ while leaving ![]() $\epsilon _2$ unchanged. Then correspondingly with the modified
$\epsilon _2$ unchanged. Then correspondingly with the modified ![]() $\mathcal {U}_1$, an integral curve in
$\mathcal {U}_1$, an integral curve in ![]() $\mathcal {U}_1\cap \{H<1\}$ must enter
$\mathcal {U}_1\cap \{H<1\}$ must enter ![]() $\mathcal {U}_2$. Since
$\mathcal {U}_2$. Since ![]() $\gamma _\infty$ converges to
$\gamma _\infty$ converges to ![]() $A_0^+$, there exists a point
$A_0^+$, there exists a point ![]() $q\in \gamma _\infty \cap \mathcal {U}_1$. By the continuous dependence, there exists a large enough
$q\in \gamma _\infty \cap \mathcal {U}_1$. By the continuous dependence, there exists a large enough ![]() $N$ such that
$N$ such that ![]() $s_1>N$ implies
$s_1>N$ implies ![]() $\gamma _{s_1}$ must enter
$\gamma _{s_1}$ must enter ![]() $\mathcal {U}_1\cap \{H<1\}$ and hence
$\mathcal {U}_1\cap \{H<1\}$ and hence ![]() $\mathcal {U}_0$.
$\mathcal {U}_0$.
Note that proving Lemma 5.7 for ![]() $m=1$ is more subtle. As
$m=1$ is more subtle. As ![]() $\gamma _\infty$ converges to
$\gamma _\infty$ converges to ![]() $B_0^+$ and there is an obvious integral curve that joins
$B_0^+$ and there is an obvious integral curve that joins ![]() $B_0^+$ and
$B_0^+$ and ![]() $A_0^+$, a more delicate analysis is needed to show that
$A_0^+$, a more delicate analysis is needed to show that ![]() $\gamma _{s_1}$ with a large enough
$\gamma _{s_1}$ with a large enough ![]() $s_1$ must enter
$s_1$ must enter ![]() $U_0$. On the other hand, since
$U_0$. On the other hand, since ![]() $\zeta _{\infty }$ converges to
$\zeta _{\infty }$ converges to ![]() $A_1^+$ for
$A_1^+$ for ![]() $m\geq 1$, we have the following corollary to Lemma 5.7.
$m\geq 1$, we have the following corollary to Lemma 5.7.
Corollary 5.8 For ![]() $m\geq 1$, the number
$m\geq 1$, the number ![]() $\theta _*+\pi$ is the limiting winding angle of
$\theta _*+\pi$ is the limiting winding angle of ![]() $\zeta _{s_2}$ around
$\zeta _{s_2}$ around ![]() $\Phi$ while
$\Phi$ while ![]() $H>0$ as
$H>0$ as ![]() $s_2\to \infty$.
$s_2\to \infty$.
Lemma 5.9 For ![]() $m\geq 2$, there exist at least two Einstein metrics on
$m\geq 2$, there exist at least two Einstein metrics on ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ if
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ if ![]() $\theta _*< \pi$. For
$\theta _*< \pi$. For ![]() $m\geq 1$, there exist at least two Einstein metrics on
$m\geq 1$, there exist at least two Einstein metrics on ![]() $\mathbb {S}^{4m+4}$ if
$\mathbb {S}^{4m+4}$ if ![]() $\theta _*> \pi$.
$\theta _*> \pi$.
Proof. Consider ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ for
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ for ![]() $m\geq 2$. Let
$m\geq 2$. Let ![]() $\tilde {s}_1=\max \{ {3}/({m-1}),s_\star \}$, where
$\tilde {s}_1=\max \{ {3}/({m-1}),s_\star \}$, where ![]() $\gamma _{s_\star }$ is the heterocline in the proof of Theorem 1.1 that joins
$\gamma _{s_\star }$ is the heterocline in the proof of Theorem 1.1 that joins ![]() $p_0^\pm$. The proof of Theorem 1.1 shows that we have
$p_0^\pm$. The proof of Theorem 1.1 shows that we have ![]() $\sharp C(\gamma _{s_1})\geq 1$ for
$\sharp C(\gamma _{s_1})\geq 1$ for ![]() $s_1\in (\tilde {s}_1, {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)})$. If
$s_1\in (\tilde {s}_1, {9(5m+3)(4m^2+4m+3)}/{n^2(2m+3)(m-1)})$. If ![]() $\theta _*< \pi$, then
$\theta _*< \pi$, then ![]() $\lim _{s_1\to \infty } \sharp C(\gamma _{s_1})=0$ by Lemma 5.7. By Theorem 4.11 there exists a heterocline
$\lim _{s_1\to \infty } \sharp C(\gamma _{s_1})=0$ by Lemma 5.7. By Theorem 4.11 there exists a heterocline ![]() $\gamma _{s_{\star \star }}$ for some
$\gamma _{s_{\star \star }}$ for some ![]() $s_{\star \star }\in \big (\tilde {s}_1,\infty \big )$ and
$s_{\star \star }\in \big (\tilde {s}_1,\infty \big )$ and ![]() $s_{\star \star }\neq s_\star$.
$s_{\star \star }\neq s_\star$.
Consider ![]() $\mathbb {S}^{4m+4}$ for
$\mathbb {S}^{4m+4}$ for ![]() $m\geq 1$. If
$m\geq 1$. If ![]() $\theta _*>\pi$, then
$\theta _*>\pi$, then ![]() $\Pi +(0,0,\pi,(2m+3)z_0)$ is an integral curve that emanates from
$\Pi +(0,0,\pi,(2m+3)z_0)$ is an integral curve that emanates from ![]() $A_1^+$ and passes
$A_1^+$ and passes ![]() $(0,0,\theta _*+\pi,(2m+3)z_0)$ and
$(0,0,\theta _*+\pi,(2m+3)z_0)$ and ![]() $\theta _*+\pi >2\pi$. By Proposition 4.10, any
$\theta _*+\pi >2\pi$. By Proposition 4.10, any ![]() $\zeta _{s_2}$ with
$\zeta _{s_2}$ with ![]() $s_2>0$ has either a turning point or a
$s_2>0$ has either a turning point or a ![]() $W$-intersection point. We learn from the linearized solution (3.6) that along
$W$-intersection point. We learn from the linearized solution (3.6) that along ![]() $\zeta _{s_2}$ with
$\zeta _{s_2}$ with ![]() $s_2> 0$ the functions
$s_2> 0$ the functions ![]() $Y-Z$ and
$Y-Z$ and ![]() $X_2-X_1$ are positive initially. Since
$X_2-X_1$ are positive initially. Since ![]() $( {Y}/{Z})'=2 ({Y}/{Z})(X_2-X_1)$ by (3.9), the function
$( {Y}/{Z})'=2 ({Y}/{Z})(X_2-X_1)$ by (3.9), the function ![]() $Y-Z=Z( {Y}/{Z}-1)$ can only have a zero after
$Y-Z=Z( {Y}/{Z}-1)$ can only have a zero after ![]() $X_2-X_1$ changes sign. In particular, the function
$X_2-X_1$ changes sign. In particular, the function ![]() $X_2-X_1$ must vanish first before any
$X_2-X_1$ must vanish first before any ![]() $W$-intersection point can occur.
$W$-intersection point can occur.
Replace ![]() $(s_1,\gamma _{s_1})$ by
$(s_1,\gamma _{s_1})$ by ![]() $(s_2,\zeta _{s_2})$ in Definition 4.8 and Theorem 4.11. For
$(s_2,\zeta _{s_2})$ in Definition 4.8 and Theorem 4.11. For ![]() $\theta _*>\pi$ we have
$\theta _*>\pi$ we have ![]() $\lim _{s_2\to \infty }\sharp C(\zeta _{s_2})\geq 1$ by Corollary 5.8. On the other hand, from Proposition 4.12 we know that
$\lim _{s_2\to \infty }\sharp C(\zeta _{s_2})\geq 1$ by Corollary 5.8. On the other hand, from Proposition 4.12 we know that ![]() $X_2-X_1> 0$ along
$X_2-X_1> 0$ along ![]() $\zeta _{ {1}/({2m+6})}$ and hence
$\zeta _{ {1}/({2m+6})}$ and hence ![]() $\sharp C(\zeta _{ {1}/({2m+6})})=0$. By Theorem 4.11 there exists some
$\sharp C(\zeta _{ {1}/({2m+6})})=0$. By Theorem 4.11 there exists some ![]() $s_\bullet \in ( {1}/({2m+6}),\infty )$ such that
$s_\bullet \in ( {1}/({2m+6}),\infty )$ such that ![]() $\zeta _{s_\bullet }$ is a heterocline.
$\zeta _{s_\bullet }$ is a heterocline.
Assume ![]() $\theta _*>\pi$ so that such an
$\theta _*>\pi$ so that such an ![]() $s_\bullet$ exists. We claim that the Einstein metric
$s_\bullet$ exists. We claim that the Einstein metric ![]() $\hat {g}_{\mathbb {S}^{4m+4}}$ represented by
$\hat {g}_{\mathbb {S}^{4m+4}}$ represented by ![]() $\zeta _{s_\bullet }$ is not the standard sphere metric. If
$\zeta _{s_\bullet }$ is not the standard sphere metric. If ![]() $\hat {g}_{\mathbb {S}^{4m+4}}$ were the standard sphere metric, it would have constant sectional curvature. In particular, we must have
$\hat {g}_{\mathbb {S}^{4m+4}}$ were the standard sphere metric, it would have constant sectional curvature. In particular, we must have ![]() $ ({\ddot {f_2}}/{f_2}) ({f_1}/{\ddot {f_1}})=1$. From (3.7) we must have
$ ({\ddot {f_2}}/{f_2}) ({f_1}/{\ddot {f_1}})=1$. From (3.7) we must have ![]() $s_2=0$. Hence,
$s_2=0$. Hence, ![]() $\hat {g}_{\mathbb {S}^{4m+4}}$ is not the standard sphere metric. The proof is complete.
$\hat {g}_{\mathbb {S}^{4m+4}}$ is not the standard sphere metric. The proof is complete.
From Lemma 5.9 we learn that the number ![]() $\theta _*$ plays an important role in proving the existence of Einstein metrics on
$\theta _*$ plays an important role in proving the existence of Einstein metrics on ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ and
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ and ![]() $\mathbb {S}^{4m+4}$. We can apply the Runge–Kutta algorithm to estimate
$\mathbb {S}^{4m+4}$. We can apply the Runge–Kutta algorithm to estimate ![]() $\Pi$. Then one can only set the initial step near
$\Pi$. Then one can only set the initial step near ![]() $A_0^+$, making the approximation less accurate as
$A_0^+$, making the approximation less accurate as ![]() $m$ increases. To bypass this issue, we make use of the symmetry of (5.7) and estimate
$m$ increases. To bypass this issue, we make use of the symmetry of (5.7) and estimate ![]() $\theta _*$ using the fourth-order Runge–Kutta algorithm with a well-defined initial step.
$\theta _*$ using the fourth-order Runge–Kutta algorithm with a well-defined initial step.
Now consider the ![]() $H\theta$-plane. It is obvious that (5.7) admits
$H\theta$-plane. It is obvious that (5.7) admits ![]() $\mathbb {Z}_2$-symmetry in the sign of
$\mathbb {Z}_2$-symmetry in the sign of ![]() $(H,\theta )$. The system also admits translation symmetry
$(H,\theta )$. The system also admits translation symmetry ![]() $(H,\theta )\rightarrow (H,\theta +i\pi )$ for any
$(H,\theta )\rightarrow (H,\theta +i\pi )$ for any ![]() $i\in \mathbb {Z}$. Let
$i\in \mathbb {Z}$. Let ![]() $O_i^\pm$ be either
$O_i^\pm$ be either ![]() $A_i^\pm$ or
$A_i^\pm$ or ![]() $B_i^\pm$ and correspondingly, let
$B_i^\pm$ and correspondingly, let ![]() $o_i^\pm$ be either
$o_i^\pm$ be either ![]() $a_i^\pm$ or
$a_i^\pm$ or ![]() $b_i^\pm$. Let
$b_i^\pm$. Let ![]() $\Psi$ be the integral curve with the initial condition
$\Psi$ be the integral curve with the initial condition ![]() $\Psi (0)=(0,0)$. In general, the integral curve
$\Psi (0)=(0,0)$. In general, the integral curve ![]() $\Psi$ must converge to some
$\Psi$ must converge to some ![]() $O_i^-$ with
$O_i^-$ with ![]() $i\geq 1$. By symmetry, we know that
$i\geq 1$. By symmetry, we know that ![]() $\Psi$ is defined on
$\Psi$ is defined on ![]() $\mathbb {R}$ and joins
$\mathbb {R}$ and joins ![]() $O_{-i}^+$ and
$O_{-i}^+$ and ![]() $O_i^-$. Then
$O_i^-$. Then ![]() $\Psi +(0,\pi )$ is an integral curve that joins
$\Psi +(0,\pi )$ is an integral curve that joins ![]() $O_{-i+1}^+$ and
$O_{-i+1}^+$ and ![]() $O_{i+1}^-$ and passes through
$O_{i+1}^-$ and passes through ![]() $(0,\pi )$, forming a barrier for estimating
$(0,\pi )$, forming a barrier for estimating ![]() $\theta _*$. In particular, if
$\theta _*$. In particular, if ![]() $\Psi$ converges to
$\Psi$ converges to ![]() $O_1^-$, then we have
$O_1^-$, then we have ![]() $o_1^-<\pi$. Then
$o_1^-<\pi$. Then ![]() $\Psi +(0,\pi )$ passes
$\Psi +(0,\pi )$ passes ![]() $(0,\pi )$ and joins either
$(0,\pi )$ and joins either ![]() $A_0^+$ and
$A_0^+$ and ![]() $A_2^-$ or
$A_2^-$ or ![]() $B_0^+$ and
$B_0^+$ and ![]() $B_2^-$. In both cases, the integral curve
$B_2^-$. In both cases, the integral curve ![]() $\Pi$ passes through
$\Pi$ passes through ![]() $(0,\theta _*)$ for some
$(0,\theta _*)$ for some ![]() $\theta _*\leq \pi$. On the other hand, if
$\theta _*\leq \pi$. On the other hand, if ![]() $\Psi$ converges to
$\Psi$ converges to ![]() $O_i^-$ with
$O_i^-$ with ![]() $i\geq 2$, then
$i\geq 2$, then ![]() $\Psi +(0,\pi )$ passes
$\Psi +(0,\pi )$ passes ![]() $(0,\pi )$ and joins
$(0,\pi )$ and joins ![]() $O_{-i+1}^+$ and
$O_{-i+1}^+$ and ![]() $O_{i+1}^-$. But
$O_{i+1}^-$. But ![]() $o_{-i+1}^+< a_0^-$, hence
$o_{-i+1}^+< a_0^-$, hence ![]() $\Pi$ passes through
$\Pi$ passes through ![]() $(0,\theta _*)$ for some
$(0,\theta _*)$ for some ![]() $\theta _*> \pi$. We present two sets of graphs on
$\theta _*> \pi$. We present two sets of graphs on ![]() $H\theta$-plane for
$H\theta$-plane for ![]() $\Psi$ and
$\Psi$ and ![]() $\Psi +(0,\pi )$ in Figure 1 to illustrate our argument. Note that if
$\Psi +(0,\pi )$ in Figure 1 to illustrate our argument. Note that if ![]() $\Psi$ converges to
$\Psi$ converges to ![]() $A_1^-$, then
$A_1^-$, then ![]() $\Pi =\Psi +(0,\pi )$ and we have
$\Pi =\Psi +(0,\pi )$ and we have ![]() $\theta _*=\pi$. In such a situation, a more delicate analysis is needed to obtain
$\theta _*=\pi$. In such a situation, a more delicate analysis is needed to obtain ![]() $\lim _{s_1\to \infty } \sharp C(\gamma _{s_1})$ and
$\lim _{s_1\to \infty } \sharp C(\gamma _{s_1})$ and ![]() $\lim _{s_2\to \infty } \sharp C(\zeta _{s_2})$. In fact, Lemma 5.9 implies that as long as
$\lim _{s_2\to \infty } \sharp C(\zeta _{s_2})$. In fact, Lemma 5.9 implies that as long as ![]() $\Psi$ does not converge to
$\Psi$ does not converge to ![]() $A_1^-$ for a fixed
$A_1^-$ for a fixed ![]() $m$, we have either a second Einstein metric on
$m$, we have either a second Einstein metric on ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ or a new Einstein metric on
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ or a new Einstein metric on ![]() $\mathbb {S}^{4m+4}$.
$\mathbb {S}^{4m+4}$.
Fortunately, the fourth-order Runge–Kutta algorithm shows that for ![]() $m\in [2,100]$, the integral curve
$m\in [2,100]$, the integral curve ![]() $\Psi$ converges to
$\Psi$ converges to ![]() $B_1^-$. Hence,
$B_1^-$. Hence, ![]() $\Pi$ must pass
$\Pi$ must pass ![]() $(0,\theta _*)$ for some
$(0,\theta _*)$ for some ![]() $\theta _*<\pi$. Therefore, by Lemma 5.9, the second Einstein metric exists on
$\theta _*<\pi$. Therefore, by Lemma 5.9, the second Einstein metric exists on ![]() $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ for
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ for ![]() $m\in [2,100]$. The function
$m\in [2,100]$. The function ![]() $H$ in (5.7) can be solved explicitly. By Remark 2.4, it is clear that
$H$ in (5.7) can be solved explicitly. By Remark 2.4, it is clear that ![]() $H=-\tanh ( {2\eta }/{n})$. Hence, the above discussion can be summarized into a more compact statement as in Theorem 1.2. Since
$H=-\tanh ( {2\eta }/{n})$. Hence, the above discussion can be summarized into a more compact statement as in Theorem 1.2. Since ![]() $\Psi$ converges to one of the
$\Psi$ converges to one of the ![]() $O_i^-$, from (5.9) the inequality
$O_i^-$, from (5.9) the inequality ![]() $\Omega < {3\pi }/{4}$ in Theorem 1.2 essentially means that
$\Omega < {3\pi }/{4}$ in Theorem 1.2 essentially means that ![]() $\Psi$ converges to
$\Psi$ converges to ![]() $B_1^-$. As shown by the algorithm, for
$B_1^-$. As shown by the algorithm, for ![]() $m=1$ the integral curve
$m=1$ the integral curve ![]() $\Psi$ converges to
$\Psi$ converges to ![]() $B_2^-$, meaning that
$B_2^-$, meaning that ![]() $\Pi$ must pass
$\Pi$ must pass ![]() $(0,\theta _*)$ for some
$(0,\theta _*)$ for some ![]() $\theta _*>\pi$. We show some plots of
$\theta _*>\pi$. We show some plots of ![]() $\Psi$ for different
$\Psi$ for different ![]() $m$ on the
$m$ on the ![]() $H\theta$-plane in Figure 2, generated by the fourth-order Runge–Kutta algorithm with step size 0.01 in Grapher.
$H\theta$-plane in Figure 2, generated by the fourth-order Runge–Kutta algorithm with step size 0.01 in Grapher.

Figure 1. Each graph shows the horizontal line ![]() $\theta =\pi$ and the level curve
$\theta =\pi$ and the level curve ![]() $2\sqrt {(2m+2)(2m+3)}z_0- (({n-1})/{n})H\sin (\theta )\cos (\theta )=0$. The cross at
$2\sqrt {(2m+2)(2m+3)}z_0- (({n-1})/{n})H\sin (\theta )\cos (\theta )=0$. The cross at ![]() $\{H=1\}$ is
$\{H=1\}$ is ![]() $A_0^+$. The plots show that for
$A_0^+$. The plots show that for ![]() $m=1$, the graph of
$m=1$, the graph of ![]() $\Pi$ must be above
$\Pi$ must be above ![]() $\Psi +(0,\pi )$ and hence
$\Psi +(0,\pi )$ and hence ![]() $\theta _*>\pi$. On the other hand, for
$\theta _*>\pi$. On the other hand, for ![]() $m=5$, the graph of
$m=5$, the graph of ![]() $\Pi$ is below
$\Pi$ is below ![]() $\Psi +(0,\pi )$ and hence
$\Psi +(0,\pi )$ and hence ![]() $\theta _*<\pi$. (a)
$\theta _*<\pi$. (a) ![]() $m=1,\ \Psi (\eta ), \eta \geq 0$. (b)
$m=1,\ \Psi (\eta ), \eta \geq 0$. (b) ![]() $m=1,\ \Psi (\eta ), \eta \in \mathbb {R}$. (c)
$m=1,\ \Psi (\eta ), \eta \in \mathbb {R}$. (c) ![]() $m=1,\ \Psi (\eta )+(0,\pi ), \eta \in \mathbb {R}$. (d)
$m=1,\ \Psi (\eta )+(0,\pi ), \eta \in \mathbb {R}$. (d) ![]() $m=5,\ \Psi (\eta ), \eta \geq 0$. (e)
$m=5,\ \Psi (\eta ), \eta \geq 0$. (e) ![]() $m=5,\ \Psi (\eta ), \eta \in \mathbb {R}$. (f)
$m=5,\ \Psi (\eta ), \eta \in \mathbb {R}$. (f) ![]() $m=5,\ \Psi (\eta )+(0,\pi ), \eta \in \mathbb {R}$.
$m=5,\ \Psi (\eta )+(0,\pi ), \eta \in \mathbb {R}$.

Figure 2. (a) ![]() $m=1$. (b)
$m=1$. (b) ![]() $m=2$. (c)
$m=2$. (c) ![]() $m=5$. (d)
$m=5$. (d) ![]() $m=10$. (e)
$m=10$. (e) ![]() $m=29$. (f)
$m=29$. (f) ![]() $m=100$.
$m=100$.
In the following lemma, we prove that ![]() $\Omega >\pi$ for
$\Omega >\pi$ for ![]() $m=1$. Therefore, the inequality
$m=1$. Therefore, the inequality ![]() $\theta _*>\pi$ is indeed valid for
$\theta _*>\pi$ is indeed valid for ![]() $m=1$.
$m=1$.
Lemma 5.10 Let ![]() $\Psi$ be an integral curve to the dynamical system
$\Psi$ be an integral curve to the dynamical system
 \begin{equation} \begin{bmatrix} H\\ \theta \end{bmatrix}'=\tilde{V}(H,\theta):= \begin{bmatrix} (H^2-1)\dfrac{1}{7}\\ \dfrac{4\sqrt{5}}{21}-\dfrac{3}{7}H\sin(2\theta) \end{bmatrix} \end{equation}
\begin{equation} \begin{bmatrix} H\\ \theta \end{bmatrix}'=\tilde{V}(H,\theta):= \begin{bmatrix} (H^2-1)\dfrac{1}{7}\\ \dfrac{4\sqrt{5}}{21}-\dfrac{3}{7}H\sin(2\theta) \end{bmatrix} \end{equation}
with ![]() $\Psi (0)=(0,0)$. Then
$\Psi (0)=(0,0)$. Then ![]() $\lim _{\eta \to \infty }\theta (\Psi ) >\pi$.
$\lim _{\eta \to \infty }\theta (\Psi ) >\pi$.
Proof. Let ![]() $H_1= {2}/({e^{ {\sqrt {5}\pi }/{6}}+1})-1\approx -0.527$ and
$H_1= {2}/({e^{ {\sqrt {5}\pi }/{6}}+1})-1\approx -0.527$ and ![]() $H_2= {2}/({\pi -2-2a_1^-})\approx -0.543$. Define the function
$H_2= {2}/({\pi -2-2a_1^-})\approx -0.543$. Define the function
 \[ \Theta(H)=\left\{\begin{array}{@{}ll}
\dfrac{1}{H}+1+a_1^-, & -1\leq H\leq
H_2,\\ \dfrac{\pi}{2}, & H_2< H<
H_1,\\
\dfrac{3\sqrt{5}}{5}\ln\left(\dfrac{1-H}{1+H}\right),
& H_1\leq H\leq 0. \end{array}\right.
\]
\[ \Theta(H)=\left\{\begin{array}{@{}ll}
\dfrac{1}{H}+1+a_1^-, & -1\leq H\leq
H_2,\\ \dfrac{\pi}{2}, & H_2< H<
H_1,\\
\dfrac{3\sqrt{5}}{5}\ln\left(\dfrac{1-H}{1+H}\right),
& H_1\leq H\leq 0. \end{array}\right.
\]
Recall that in (5.8) we have ![]() $a_1^-=\pi -\arctan\ ({2\sqrt {5}}/{5})$. Then we have
$a_1^-=\pi -\arctan\ ({2\sqrt {5}}/{5})$. Then we have
The function ![]() $\Theta$ is non-increasing. The numbers
$\Theta$ is non-increasing. The numbers ![]() $H_1$ and
$H_1$ and ![]() $H_2$ are chosen so that
$H_2$ are chosen so that ![]() $\{\theta -\Theta (H)=0\}$ is a continuous curve that joins the origin and
$\{\theta -\Theta (H)=0\}$ is a continuous curve that joins the origin and ![]() $A_1^-$.
$A_1^-$.
We show that ![]() $\tilde {V}$ restricted to
$\tilde {V}$ restricted to ![]() $\{\theta -\Theta (H)=0\}$ points upward. For
$\{\theta -\Theta (H)=0\}$ points upward. For ![]() $(H,\theta )\in (H_1,0)\times (0, {\pi }/{2})$, we have
$(H,\theta )\in (H_1,0)\times (0, {\pi }/{2})$, we have
 \begin{align} \left\langle \nabla\left(\theta-\frac{3\sqrt{5}}{5}\ln \left(\frac{1-H}{1+H}\right)\right),\tilde{V}\right\rangle &= \frac{4\sqrt{5}}{21}-\frac{3}{7}H\sin(2\theta)+\frac{6\sqrt{5}}{5}\frac{1}{1-H^2}\frac{H^2-1}{7} \nonumber\\ &=\frac{2\sqrt{5}}{105}-\frac{3}{7}H\sin(2\theta) \nonumber\\ &> 0. \end{align}
\begin{align} \left\langle \nabla\left(\theta-\frac{3\sqrt{5}}{5}\ln \left(\frac{1-H}{1+H}\right)\right),\tilde{V}\right\rangle &= \frac{4\sqrt{5}}{21}-\frac{3}{7}H\sin(2\theta)+\frac{6\sqrt{5}}{5}\frac{1}{1-H^2}\frac{H^2-1}{7} \nonumber\\ &=\frac{2\sqrt{5}}{105}-\frac{3}{7}H\sin(2\theta) \nonumber\\ &> 0. \end{align}
Therefore, the function ![]() $\theta -\Theta (H)$ remains positive along
$\theta -\Theta (H)$ remains positive along ![]() $\Psi$ as
$\Psi$ as ![]() $H$ decreases from
$H$ decreases from ![]() $0$ to
$0$ to ![]() $H_1$. The computation above also shows that the function
$H_1$. The computation above also shows that the function ![]() $\theta -\Theta (H)$ is positive along
$\theta -\Theta (H)$ is positive along ![]() $\Psi (\eta )$ once the integral curve leaves the origin. If
$\Psi (\eta )$ once the integral curve leaves the origin. If ![]() $\theta = {\pi }/{2}$, then
$\theta = {\pi }/{2}$, then ![]() $\langle \nabla \theta,\tilde {V}\rangle = {4\sqrt {5}}/{21}>0.$ Hence,
$\langle \nabla \theta,\tilde {V}\rangle = {4\sqrt {5}}/{21}>0.$ Hence, ![]() $\theta > {\pi }/{2}$ along
$\theta > {\pi }/{2}$ along ![]() $\Psi$ as
$\Psi$ as ![]() $H$ decreases from
$H$ decreases from ![]() $H_1$ to
$H_1$ to ![]() $H_2$.
$H_2$.
Finally, as ![]() $H$ decreases from
$H$ decreases from ![]() $H_2$ to
$H_2$ to ![]() $-1$, the function
$-1$, the function ![]() $\Theta (H)$ increases from
$\Theta (H)$ increases from ![]() $ {\pi }/{2}$ to
$ {\pi }/{2}$ to ![]() $a_1^-$. We first claim that for
$a_1^-$. We first claim that for ![]() $\theta \in [ {\pi }/{2},a_1^-]$, the inequality
$\theta \in [ {\pi }/{2},a_1^-]$, the inequality
is valid. It is obvious that ![]() $D(a_1^-)=D( {\pi }/{2})=0$. Hence, there exists some
$D(a_1^-)=D( {\pi }/{2})=0$. Hence, there exists some ![]() $\theta _1\in ( {\pi }/{2},a_1^-)$ such that
$\theta _1\in ( {\pi }/{2},a_1^-)$ such that ![]() $D'(\theta _1)=0$ by the mean value theorem. On the other hand, we have
$D'(\theta _1)=0$ by the mean value theorem. On the other hand, we have
Hence, ![]() $D''>0$ on
$D''>0$ on ![]() $( {\pi }/{2}+\frac {1}{2}\arcsin (\frac {7}{8}),\pi -\frac {1}{2}\arcsin (\frac {7}{8}))$. Since
$( {\pi }/{2}+\frac {1}{2}\arcsin (\frac {7}{8}),\pi -\frac {1}{2}\arcsin (\frac {7}{8}))$. Since ![]() $\pi -\frac {1}{2}\arcsin (\frac {7}{8})\approx 2.609> 2.412\approx a_1^-$, it is clear that
$\pi -\frac {1}{2}\arcsin (\frac {7}{8})\approx 2.609> 2.412\approx a_1^-$, it is clear that ![]() $D'$ decreases in
$D'$ decreases in ![]() $( {\pi }/{2}, {\pi }/{2}+\frac {1}{2}\arcsin (\frac {7}{8}))$ and increases in
$( {\pi }/{2}, {\pi }/{2}+\frac {1}{2}\arcsin (\frac {7}{8}))$ and increases in ![]() $( {\pi }/{2}+\frac {1}{2}\arcsin (\frac {7}{8}),a_1^-)$. Since
$( {\pi }/{2}+\frac {1}{2}\arcsin (\frac {7}{8}),a_1^-)$. Since
 \begin{equation} \begin{aligned} & D'\left(\frac{\pi}{2}\right)=-2-\left(\frac{7}{4} \left(\frac{\pi}{2}-a_1^-\right)+\frac{\sin(2a_1^-)}{a_1^--{\pi}/{2}}\right)\approx 0.654 >0,\\ & D'(a_1^-)=2\cos(2a_1^-)-\frac{\sin(2a_1^-)}{a_1^--{\pi}/{2}}-\frac{7}{4} \left(a_1^- -\frac{\pi}{2}\right)\approx -0.068 <0, \end{aligned}\end{equation}
\begin{equation} \begin{aligned} & D'\left(\frac{\pi}{2}\right)=-2-\left(\frac{7}{4} \left(\frac{\pi}{2}-a_1^-\right)+\frac{\sin(2a_1^-)}{a_1^--{\pi}/{2}}\right)\approx 0.654 >0,\\ & D'(a_1^-)=2\cos(2a_1^-)-\frac{\sin(2a_1^-)}{a_1^--{\pi}/{2}}-\frac{7}{4} \left(a_1^- -\frac{\pi}{2}\right)\approx -0.068 <0, \end{aligned}\end{equation}
we know that ![]() $D'$ only vanishes once in
$D'$ only vanishes once in ![]() $[ {\pi }/{2},a_1^-]$. Therefore, the function
$[ {\pi }/{2},a_1^-]$. Therefore, the function ![]() $D$ is indeed positive for
$D$ is indeed positive for ![]() $\theta \in ( {\pi }/{2},a_1^-)$.
$\theta \in ( {\pi }/{2},a_1^-)$.
Then from (5.13) we have
 \begin{align} & \left\langle
\nabla\left(\theta-\frac{1}{H}-1-a_1^-\right),
\tilde{V}\right\rangle \left |_{\theta-{1}/{H}-1-a_1^-=
0}\right. \nonumber\\ &\quad
=\frac{4\sqrt{5}}{21}-\frac{3}{7}H\sin(2\theta)+\frac{1}{7H^2}(H^2-1)
\nonumber\\ &\quad \geq
\frac{4\sqrt{5}}{21}-\frac{3}{7}H\left(\theta-\frac{\pi}{2}\right)
\left(\frac{7}{4}(\theta-a_1^-)+\frac{\sin(2a_1^-)}{a_1^-
-{\pi}/{2}}\right)+ \frac{1}{7H^2}(H^2-1) \nonumber\\
&\quad
=\frac{4\sqrt{5}}{21}-\frac{3}{7}H\left(\frac{1+H}{H}+a_1^--\frac{\pi}{2}\right)
\left(\frac{7}{4}\left(\frac{1+H}{H}\right)+\frac{\sin(2a_1^-)}{a_1^-
-{\pi}/{2}}\right)+ \frac{1}{7H^2}(H^2-1) \nonumber\\
&\qquad \text{since $\theta-\frac{1}{H}-1-a_1^-= 0$}
\nonumber\\ &\quad =
\frac{4\sqrt{5}}{21}(1+H)-\left(\frac{3}{4}
\left(a_1^--\frac{\pi}{2}\right)+\frac{3}{7}\frac{\sin(2a_1^-)}{a_1^-
-{\pi}/{2}}\right)
(1+H)-\frac{3}{4}\frac{(1+H)^2}{H}+\frac{1}{7H^2}(H^2-1).
\end{align}
\begin{align} & \left\langle
\nabla\left(\theta-\frac{1}{H}-1-a_1^-\right),
\tilde{V}\right\rangle \left |_{\theta-{1}/{H}-1-a_1^-=
0}\right. \nonumber\\ &\quad
=\frac{4\sqrt{5}}{21}-\frac{3}{7}H\sin(2\theta)+\frac{1}{7H^2}(H^2-1)
\nonumber\\ &\quad \geq
\frac{4\sqrt{5}}{21}-\frac{3}{7}H\left(\theta-\frac{\pi}{2}\right)
\left(\frac{7}{4}(\theta-a_1^-)+\frac{\sin(2a_1^-)}{a_1^-
-{\pi}/{2}}\right)+ \frac{1}{7H^2}(H^2-1) \nonumber\\
&\quad
=\frac{4\sqrt{5}}{21}-\frac{3}{7}H\left(\frac{1+H}{H}+a_1^--\frac{\pi}{2}\right)
\left(\frac{7}{4}\left(\frac{1+H}{H}\right)+\frac{\sin(2a_1^-)}{a_1^-
-{\pi}/{2}}\right)+ \frac{1}{7H^2}(H^2-1) \nonumber\\
&\qquad \text{since $\theta-\frac{1}{H}-1-a_1^-= 0$}
\nonumber\\ &\quad =
\frac{4\sqrt{5}}{21}(1+H)-\left(\frac{3}{4}
\left(a_1^--\frac{\pi}{2}\right)+\frac{3}{7}\frac{\sin(2a_1^-)}{a_1^-
-{\pi}/{2}}\right)
(1+H)-\frac{3}{4}\frac{(1+H)^2}{H}+\frac{1}{7H^2}(H^2-1).
\end{align}
Since ![]() $ {4\sqrt {5}}/{21}-(\frac {3}{4}(a_1^-- {\pi }/{2})+\frac {3}{7} ({\sin (2a_1^-)}/({a_1^- - {\pi }/{2}}))\approx 0.3015 >0.3$, the computation above continues as
$ {4\sqrt {5}}/{21}-(\frac {3}{4}(a_1^-- {\pi }/{2})+\frac {3}{7} ({\sin (2a_1^-)}/({a_1^- - {\pi }/{2}}))\approx 0.3015 >0.3$, the computation above continues as
 \begin{align} \left\langle \nabla\left(\theta-\frac{1}{H}-1-a_1^-\right), \tilde{V}\right\rangle\left|_{\theta-{1}/{H}-1-a_1^-= 0}\right. &\geq \frac{3}{10}(1+H)-\frac{3}{4}\frac{(1+H)^2}{H}+\frac{1}{7H^2}(H^2-1) \nonumber\\ &=\frac{1+H}{H^2}\left(\!-\frac{9}{20}H^2-\frac{17}{28}H-\frac{1}{7}\right). \end{align}
\begin{align} \left\langle \nabla\left(\theta-\frac{1}{H}-1-a_1^-\right), \tilde{V}\right\rangle\left|_{\theta-{1}/{H}-1-a_1^-= 0}\right. &\geq \frac{3}{10}(1+H)-\frac{3}{4}\frac{(1+H)^2}{H}+\frac{1}{7H^2}(H^2-1) \nonumber\\ &=\frac{1+H}{H^2}\left(\!-\frac{9}{20}H^2-\frac{17}{28}H-\frac{1}{7}\right). \end{align}
A straightforward computation shows that the factor ![]() $-\frac {9}{20}H^2-\frac {17}{28}H-\frac {1}{7}$ is positive on
$-\frac {9}{20}H^2-\frac {17}{28}H-\frac {1}{7}$ is positive on ![]() $[-1,-\frac {1}{2}]$. As
$[-1,-\frac {1}{2}]$. As ![]() $H_2<-\frac {1}{2}$, it is proved that
$H_2<-\frac {1}{2}$, it is proved that ![]() $\Psi$ does not pass the barrier
$\Psi$ does not pass the barrier ![]() $\theta -\Theta (H)=0$ where
$\theta -\Theta (H)=0$ where ![]() $H\in (-1,H_2)$. Therefore, we must have
$H\in (-1,H_2)$. Therefore, we must have ![]() $\lim _{\eta \to \infty }\theta (\Psi )\geq a_1^-$.
$\lim _{\eta \to \infty }\theta (\Psi )\geq a_1^-$.
We claim that ![]() $\Psi$ does not converge to
$\Psi$ does not converge to ![]() $A_1^-$. The linearization of (5.11) at
$A_1^-$. The linearization of (5.11) at ![]() $A_1^-$ is
$A_1^-$ is ![]() $\Big [\begin{smallmatrix} -\frac {2}{7} & 0\\ \frac {4\sqrt {5}}{21} & \frac {2}{21} \end{smallmatrix}\Big ]$, whose only stable eigenvalue and eigenvector are respectively
$\Big [\begin{smallmatrix} -\frac {2}{7} & 0\\ \frac {4\sqrt {5}}{21} & \frac {2}{21} \end{smallmatrix}\Big ]$, whose only stable eigenvalue and eigenvector are respectively ![]() $-\frac {2}{7}$ and
$-\frac {2}{7}$ and ![]() $\Big [\begin{smallmatrix} 2\\ -\sqrt {5}\\ \end{smallmatrix}\Big ]$. Hence, the linearized solution in
$\Big [\begin{smallmatrix} 2\\ -\sqrt {5}\\ \end{smallmatrix}\Big ]$. Hence, the linearized solution in ![]() $\{H> -1\}$ takes the form
$\{H> -1\}$ takes the form ![]() $A_1^- + \Big [\begin{smallmatrix} 2\\ -\sqrt {5}\\ \end{smallmatrix}\Big ]e^{- ({2}/{7})\eta }$. Suppose
$A_1^- + \Big [\begin{smallmatrix} 2\\ -\sqrt {5}\\ \end{smallmatrix}\Big ]e^{- ({2}/{7})\eta }$. Suppose ![]() $\Psi$ is the integral curve that tends to
$\Psi$ is the integral curve that tends to ![]() $A_1^-$. We must have
$A_1^-$. We must have
as ![]() $\eta \to \infty$, which is a contradiction. Therefore, the integral curve
$\eta \to \infty$, which is a contradiction. Therefore, the integral curve ![]() $\Psi$ converges to some
$\Psi$ converges to some ![]() $O_i^-$ with
$O_i^-$ with ![]() $i\geq 2$. As
$i\geq 2$. As ![]() $A_2^->B_2^->\pi$, we conclude that
$A_2^->B_2^->\pi$, we conclude that ![]() $\lim _{\eta \to \infty }\theta (\Psi )>\pi$.
$\lim _{\eta \to \infty }\theta (\Psi )>\pi$.
Appendix A.
A.1 Coefficients for  $\tilde {B}_{m,\kappa }$ and
$\tilde {B}_{m,\kappa }$ and  $\tilde {Q}_{m,\kappa }$
$\tilde {Q}_{m,\kappa }$
We list coefficients for ![]() $\tilde {B}_{m,\kappa }$ and
$\tilde {B}_{m,\kappa }$ and ![]() $\tilde {Q}_{m,\kappa }$:
$\tilde {Q}_{m,\kappa }$:
–
 $\tilde {B}_{m,\kappa }(x)=b_2x^2+b_1x+b_0$
(A.1)
$\tilde {B}_{m,\kappa }(x)=b_2x^2+b_1x+b_0$
(A.1) \begin{equation} \begin{aligned} b_2 & =-\frac{96 \kappa^3 m^3+264 \kappa^2 m^2+216 \kappa m+54}{(1-\kappa) (2\kappa^2m(8m-5)+6\kappa(4m-1)+9)}<0,\\ b_1 & =\frac{4(m+2)(4 \kappa m+3) (2 \kappa^2 m+4 \kappa m+3)}{(1-\kappa) (2\kappa^2m(8m-5)+6\kappa(4m-1)+9)}-\frac{2 (4m+3)^2 (2 m+3) (m-1)}{m(2m+1)(8m+3)},\\ b_0 & =-\frac{3 (4+(4m-2) \kappa) (4\kappa m+3) \kappa}{(1-\kappa)(2\kappa^2m(8m-5)+6\kappa(4m-1)+9)}<0. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} b_2 & =-\frac{96 \kappa^3 m^3+264 \kappa^2 m^2+216 \kappa m+54}{(1-\kappa) (2\kappa^2m(8m-5)+6\kappa(4m-1)+9)}<0,\\ b_1 & =\frac{4(m+2)(4 \kappa m+3) (2 \kappa^2 m+4 \kappa m+3)}{(1-\kappa) (2\kappa^2m(8m-5)+6\kappa(4m-1)+9)}-\frac{2 (4m+3)^2 (2 m+3) (m-1)}{m(2m+1)(8m+3)},\\ b_0 & =-\frac{3 (4+(4m-2) \kappa) (4\kappa m+3) \kappa}{(1-\kappa)(2\kappa^2m(8m-5)+6\kappa(4m-1)+9)}<0. \end{aligned} \end{equation}–
 $\tilde {Q}_{m,\kappa }(x)=q_2x^2+q_1x+q_0$
(A.2)
$\tilde {Q}_{m,\kappa }(x)=q_2x^2+q_1x+q_0$
(A.2) \begin{equation} \begin{aligned} q_2 & =-\frac{4(2\kappa m+3)(32\kappa^3m^3+\kappa^2m^2(96-68\kappa)+ \kappa m(90-84\kappa)+27(1-\kappa))}{3(1-\kappa)(2\kappa^2m(8m-5)+6\kappa(4m-1)+9)}<0,\\ q_1 & =\frac{16 \kappa(m+2)(16 \kappa^3 m^3-18 \kappa^3 m^2+32 \kappa^2 m^2-24 \kappa^2 m+27 \kappa m-9 \kappa+9)}{3(1- \kappa)(2\kappa^2m(8m-5)+6\kappa(4m-1)+9)}>0,\\ q_0 & =-\frac{4\kappa^2(32\kappa^2m^3-20\kappa^2m^2-6\kappa^2m+48 \kappa m^2-6\kappa m-9\kappa+18m+9)}{3(1-\kappa)(2\kappa^2m(8m-5)+6\kappa(4m-1)+9)}<0. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} q_2 & =-\frac{4(2\kappa m+3)(32\kappa^3m^3+\kappa^2m^2(96-68\kappa)+ \kappa m(90-84\kappa)+27(1-\kappa))}{3(1-\kappa)(2\kappa^2m(8m-5)+6\kappa(4m-1)+9)}<0,\\ q_1 & =\frac{16 \kappa(m+2)(16 \kappa^3 m^3-18 \kappa^3 m^2+32 \kappa^2 m^2-24 \kappa^2 m+27 \kappa m-9 \kappa+9)}{3(1- \kappa)(2\kappa^2m(8m-5)+6\kappa(4m-1)+9)}>0,\\ q_0 & =-\frac{4\kappa^2(32\kappa^2m^3-20\kappa^2m^2-6\kappa^2m+48 \kappa m^2-6\kappa m-9\kappa+18m+9)}{3(1-\kappa)(2\kappa^2m(8m-5)+6\kappa(4m-1)+9)}<0. \end{aligned} \end{equation}
Proposition A.1 For any ![]() $(m,\kappa )\in [1,\infty )\times (0,1)$, the function
$(m,\kappa )\in [1,\infty )\times (0,1)$, the function ![]() $\tilde {B}_{m,\kappa }$ has a real root
$\tilde {B}_{m,\kappa }$ has a real root ![]() $\sigma (m,\kappa )$ in the interval
$\sigma (m,\kappa )$ in the interval ![]() $(0, {m\kappa }/({3+2m\kappa }))$. For
$(0, {m\kappa }/({3+2m\kappa }))$. For ![]() $m=1$, polynomials
$m=1$, polynomials ![]() $\tilde {B}_{1,\kappa }$ and
$\tilde {B}_{1,\kappa }$ and ![]() $\tilde {Q}_{1,\kappa }$ share a common real root
$\tilde {Q}_{1,\kappa }$ share a common real root ![]() $\sigma (1,\kappa )= {\kappa }/({3+2\kappa })$.
$\sigma (1,\kappa )= {\kappa }/({3+2\kappa })$.
Proof. From (A.1), computations show that
 \begin{equation} \begin{aligned} \tilde{B}_{m,\kappa}(0) & =b_0<0,\\ \tilde{B}_{m,\kappa}\left(\frac{m\kappa}{3+2m\kappa}\right) & = \frac{768(m-1)\kappa B_*}{(8m + 3) (2 \kappa m + 3) (2m + 1) (1 - \kappa) (2\kappa^2m(8m-5)+6\kappa(4m-1)+9)} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \tilde{B}_{m,\kappa}(0) & =b_0<0,\\ \tilde{B}_{m,\kappa}\left(\frac{m\kappa}{3+2m\kappa}\right) & = \frac{768(m-1)\kappa B_*}{(8m + 3) (2 \kappa m + 3) (2m + 1) (1 - \kappa) (2\kappa^2m(8m-5)+6\kappa(4m-1)+9)} \end{aligned} \end{equation}where
 \begin{align} B_*&=\left(m^4 + \frac{15}{8} m^3 + \frac{5}{16} m^2 - \frac{45}{32} m - \frac{45}{64}\right) m\kappa^3 + \left(\frac{13}{4} m^4 + \frac{163}{32} m^3 + \frac{255}{64} m^2 + \frac{9}{16} m - \frac{27}{64}\right) \kappa^2 \nonumber\\ &\quad +\left(\frac{21}{8} m^3 + \frac{147}{64} m^2 + \frac{243}{128} m + \frac{27}{32}\right) \kappa + \frac{21}{32}m^2 - \frac{27}{128} \nonumber\\ &>0 \end{align}
\begin{align} B_*&=\left(m^4 + \frac{15}{8} m^3 + \frac{5}{16} m^2 - \frac{45}{32} m - \frac{45}{64}\right) m\kappa^3 + \left(\frac{13}{4} m^4 + \frac{163}{32} m^3 + \frac{255}{64} m^2 + \frac{9}{16} m - \frac{27}{64}\right) \kappa^2 \nonumber\\ &\quad +\left(\frac{21}{8} m^3 + \frac{147}{64} m^2 + \frac{243}{128} m + \frac{27}{32}\right) \kappa + \frac{21}{32}m^2 - \frac{27}{128} \nonumber\\ &>0 \end{align}
for any ![]() $(m,\kappa )\in [1,\infty )\times (0,1)$. Hence, such a
$(m,\kappa )\in [1,\infty )\times (0,1)$. Hence, such a ![]() $\sigma (m,\kappa )$ exists. Furthermore, we have
$\sigma (m,\kappa )$ exists. Furthermore, we have
 \begin{equation} \begin{aligned} \tilde{B}_{1,\kappa}(x) & =\frac{2(3+4\kappa)((2\kappa+1)x-\kappa-2) ((2\kappa+3)x-\kappa)}{(2\kappa^2+6\kappa+3)(\kappa-1)},\\ \tilde{Q}_{1,\kappa}(x) & =-\frac{4((12\kappa^3-4\kappa^2-21\kappa-9)x+2 \kappa^3+11 \kappa^2+9 \kappa)((2\kappa+3)x-\kappa)}{3(2\kappa^2+6\kappa+3)(\kappa-1)}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \tilde{B}_{1,\kappa}(x) & =\frac{2(3+4\kappa)((2\kappa+1)x-\kappa-2) ((2\kappa+3)x-\kappa)}{(2\kappa^2+6\kappa+3)(\kappa-1)},\\ \tilde{Q}_{1,\kappa}(x) & =-\frac{4((12\kappa^3-4\kappa^2-21\kappa-9)x+2 \kappa^3+11 \kappa^2+9 \kappa)((2\kappa+3)x-\kappa)}{3(2\kappa^2+6\kappa+3)(\kappa-1)}. \end{aligned} \end{equation}The proof is complete.
A.2 Non-positivity of  $r(\tilde {Q}_{m,\kappa },\tilde {B}_{m,\kappa })$
$r(\tilde {Q}_{m,\kappa },\tilde {B}_{m,\kappa })$
Proposition A.2 The resultant ![]() $r(\tilde {Q}_{m,\kappa },\tilde {B}_{m,\kappa })$ in (4.17) is non-positive for any
$r(\tilde {Q}_{m,\kappa },\tilde {B}_{m,\kappa })$ in (4.17) is non-positive for any ![]() $(m,\kappa )\in [1,\infty )\times (0,1)$ and vanishes if and only if
$(m,\kappa )\in [1,\infty )\times (0,1)$ and vanishes if and only if ![]() $m=1$.
$m=1$.
Proof. Recall that
 \begin{align} r(\tilde{Q}_{m,\kappa},\tilde{B}_{m,\kappa})&=-\frac{64\kappa^2(m-1) (2\kappa m+3)}{(8m+3)^2(2m+1)^2m^2(1-\kappa)(2\kappa^2m(8m-5)+6\kappa(4m-1)+9)^2}\tilde{r}, \nonumber\\ \tilde{r}&=262144 \kappa ^4 m^{10}+(516096 \kappa ^4+679936 \kappa ^3) m^9 \nonumber\\ &\quad +(373760 \kappa ^4+1233920 \kappa ^3+675840 \kappa ^2) m^8 \nonumber\\ &\quad +(-275904 \kappa ^4+1151040 \kappa ^3+1143744 \kappa ^2+308160 \kappa ) m^7 \nonumber\\ &\quad +(-926496 \kappa ^4+248832 \kappa ^3+1432512 \kappa ^2+507456 \kappa +54432) m^6 \nonumber\\ &\quad +(-800496 \kappa ^4-1256256 \kappa ^3+1472688 \kappa ^2+857520 \kappa +92016) m^5 \nonumber\\ &\quad +(-281880 \kappa ^4-1525392 \kappa ^3+266328 \kappa ^2+1353024 \kappa +199584) m^4 \nonumber\\ &\quad +(-33048 \kappa ^4-644436 \kappa ^3-672624 \kappa ^2+957420 \kappa +375192) m^3 \nonumber\\ &\quad +(-90396 \kappa ^3-433026 \kappa ^2 +186624 \kappa +333882) m^2 \nonumber\\ &\quad +(-74358 \kappa ^2-59049 \kappa +133407) m+19683(1-\kappa). \end{align}
\begin{align} r(\tilde{Q}_{m,\kappa},\tilde{B}_{m,\kappa})&=-\frac{64\kappa^2(m-1) (2\kappa m+3)}{(8m+3)^2(2m+1)^2m^2(1-\kappa)(2\kappa^2m(8m-5)+6\kappa(4m-1)+9)^2}\tilde{r}, \nonumber\\ \tilde{r}&=262144 \kappa ^4 m^{10}+(516096 \kappa ^4+679936 \kappa ^3) m^9 \nonumber\\ &\quad +(373760 \kappa ^4+1233920 \kappa ^3+675840 \kappa ^2) m^8 \nonumber\\ &\quad +(-275904 \kappa ^4+1151040 \kappa ^3+1143744 \kappa ^2+308160 \kappa ) m^7 \nonumber\\ &\quad +(-926496 \kappa ^4+248832 \kappa ^3+1432512 \kappa ^2+507456 \kappa +54432) m^6 \nonumber\\ &\quad +(-800496 \kappa ^4-1256256 \kappa ^3+1472688 \kappa ^2+857520 \kappa +92016) m^5 \nonumber\\ &\quad +(-281880 \kappa ^4-1525392 \kappa ^3+266328 \kappa ^2+1353024 \kappa +199584) m^4 \nonumber\\ &\quad +(-33048 \kappa ^4-644436 \kappa ^3-672624 \kappa ^2+957420 \kappa +375192) m^3 \nonumber\\ &\quad +(-90396 \kappa ^3-433026 \kappa ^2 +186624 \kappa +333882) m^2 \nonumber\\ &\quad +(-74358 \kappa ^2-59049 \kappa +133407) m+19683(1-\kappa). \end{align}
It is clear that the coefficient for ![]() $\tilde {r}$ is non-positive on
$\tilde {r}$ is non-positive on ![]() $[1,\infty )\times (0,1)$ and vanishes if and only if
$[1,\infty )\times (0,1)$ and vanishes if and only if ![]() $m=1$.
$m=1$.
Consider the polynomial ![]() $\tilde {r}$. Since coefficients for
$\tilde {r}$. Since coefficients for ![]() $m^i$ are obviously positive for
$m^i$ are obviously positive for ![]() $k\in (0,1)$ if
$k\in (0,1)$ if ![]() $i\geq 5$, we must have
$i\geq 5$, we must have
 \begin{align} \tilde{r}&> 262144 \kappa
^4 m^4+(516096 \kappa ^4+679936 \kappa ^3) m^4+ (373760
\kappa ^4+1233920 \kappa ^3+675840 \kappa ^2) m^4
\nonumber\\ &\quad +(-275904 \kappa ^4+1151040 \kappa
^3+1143744 \kappa ^2+308160 \kappa ) m^4 \nonumber\\ &\quad
+(-926496 \kappa ^4+248832 \kappa ^3+1432512 \kappa
^2+507456 \kappa +54432) m^4 \nonumber\\ &\quad +(-800496
\kappa ^4-1256256 \kappa ^3+1472688 \kappa ^2+857520 \kappa
+92016) m^4\nonumber\\ &\quad +(-281880 \kappa ^4-1525392
\kappa ^3+266328 \kappa ^2+1353024 \kappa +199584)
m^4\nonumber\\ &\quad +(-33048 \kappa ^4-644436 \kappa
^3-672624 \kappa ^2+957420 \kappa +375192) m^3\nonumber\\
&\quad +(-90396 \kappa ^3-433026 \kappa ^2 +186624 \kappa
+333882) m^2 \nonumber\\ &\quad +(-74358 \kappa ^2-59049
\kappa +133407) m+19683(1-\kappa) \nonumber\\
&=(-1132776\kappa ^4+532080\kappa ^3+4991112\kappa
^2+3026160\kappa +346032)m^4 \nonumber\\ &\quad
+(-33048\kappa ^4-644436\kappa ^3-672624\kappa
^2+957420\kappa +375192)m^3 \nonumber\\ &\quad
+(-90396\kappa ^3-433026\kappa ^2+186624\kappa
+333882)m^2\nonumber\\ &\quad +(-74358\kappa ^2-59049\kappa
+133407)m+19683(1-\kappa)\nonumber\\ &\geq (-1132776\kappa
^4+532080\kappa ^3+4991112\kappa ^2+3026160\kappa
+346032)m^3 \nonumber\\ &\quad +(-33048\kappa
^4-644436\kappa ^3-672624\kappa ^2+957420\kappa
+375192)m^3 \nonumber\\ &\quad +(-90396\kappa
^3-433026\kappa ^2+186624\kappa +333882)m^2\nonumber\\
&\quad +(-74358\kappa ^2-59049\kappa
+133407)m+19683(1-\kappa)\nonumber\\
&=(-1165824\kappa^4-112356\kappa^3+4318488\kappa^2+3983580\kappa+721224)m^3\nonumber\\
&\quad
+(-90396\kappa^3-433026\kappa^2+186624\kappa+333882)m^2\nonumber\\
&\quad
+(-74358\kappa^2-59049\kappa+133407)m+19683(1-\kappa)\nonumber\\
&\geq
(-1165824\kappa^4-112356\kappa^3+4318488\kappa^2+3983580\kappa+721224)m^2\nonumber\\
&\quad
+(-90396\kappa^3-433026\kappa^2+186624\kappa+333882)m^2\nonumber\\
&\quad
+(-74358\kappa^2-59049\kappa+133407)m+19683(1-\kappa)\nonumber\\
&=(-1165824\kappa^4-202752\kappa^3+3885462\kappa^2+4170204\kappa+1055106)m^2\nonumber\\
&\quad
+(-74358\kappa^2-59049\kappa+133407)m+19683(1-\kappa)\nonumber\\
&> 0. \end{align}
\begin{align} \tilde{r}&> 262144 \kappa
^4 m^4+(516096 \kappa ^4+679936 \kappa ^3) m^4+ (373760
\kappa ^4+1233920 \kappa ^3+675840 \kappa ^2) m^4
\nonumber\\ &\quad +(-275904 \kappa ^4+1151040 \kappa
^3+1143744 \kappa ^2+308160 \kappa ) m^4 \nonumber\\ &\quad
+(-926496 \kappa ^4+248832 \kappa ^3+1432512 \kappa
^2+507456 \kappa +54432) m^4 \nonumber\\ &\quad +(-800496
\kappa ^4-1256256 \kappa ^3+1472688 \kappa ^2+857520 \kappa
+92016) m^4\nonumber\\ &\quad +(-281880 \kappa ^4-1525392
\kappa ^3+266328 \kappa ^2+1353024 \kappa +199584)
m^4\nonumber\\ &\quad +(-33048 \kappa ^4-644436 \kappa
^3-672624 \kappa ^2+957420 \kappa +375192) m^3\nonumber\\
&\quad +(-90396 \kappa ^3-433026 \kappa ^2 +186624 \kappa
+333882) m^2 \nonumber\\ &\quad +(-74358 \kappa ^2-59049
\kappa +133407) m+19683(1-\kappa) \nonumber\\
&=(-1132776\kappa ^4+532080\kappa ^3+4991112\kappa
^2+3026160\kappa +346032)m^4 \nonumber\\ &\quad
+(-33048\kappa ^4-644436\kappa ^3-672624\kappa
^2+957420\kappa +375192)m^3 \nonumber\\ &\quad
+(-90396\kappa ^3-433026\kappa ^2+186624\kappa
+333882)m^2\nonumber\\ &\quad +(-74358\kappa ^2-59049\kappa
+133407)m+19683(1-\kappa)\nonumber\\ &\geq (-1132776\kappa
^4+532080\kappa ^3+4991112\kappa ^2+3026160\kappa
+346032)m^3 \nonumber\\ &\quad +(-33048\kappa
^4-644436\kappa ^3-672624\kappa ^2+957420\kappa
+375192)m^3 \nonumber\\ &\quad +(-90396\kappa
^3-433026\kappa ^2+186624\kappa +333882)m^2\nonumber\\
&\quad +(-74358\kappa ^2-59049\kappa
+133407)m+19683(1-\kappa)\nonumber\\
&=(-1165824\kappa^4-112356\kappa^3+4318488\kappa^2+3983580\kappa+721224)m^3\nonumber\\
&\quad
+(-90396\kappa^3-433026\kappa^2+186624\kappa+333882)m^2\nonumber\\
&\quad
+(-74358\kappa^2-59049\kappa+133407)m+19683(1-\kappa)\nonumber\\
&\geq
(-1165824\kappa^4-112356\kappa^3+4318488\kappa^2+3983580\kappa+721224)m^2\nonumber\\
&\quad
+(-90396\kappa^3-433026\kappa^2+186624\kappa+333882)m^2\nonumber\\
&\quad
+(-74358\kappa^2-59049\kappa+133407)m+19683(1-\kappa)\nonumber\\
&=(-1165824\kappa^4-202752\kappa^3+3885462\kappa^2+4170204\kappa+1055106)m^2\nonumber\\
&\quad
+(-74358\kappa^2-59049\kappa+133407)m+19683(1-\kappa)\nonumber\\
&> 0. \end{align}
Since ![]() $\tilde {r}$ is positive on
$\tilde {r}$ is positive on ![]() $[1,\infty )\times (0,1)$, the proof is complete.
$[1,\infty )\times (0,1)$, the proof is complete.

Figure A.1. The set ![]() $\mathcal {S}$ is degenerate as shown in Proposition 4.2. Hence, only one integral curve
$\mathcal {S}$ is degenerate as shown in Proposition 4.2. Hence, only one integral curve ![]() $\gamma _{s_\star}\!$ is known to join
$\gamma _{s_\star}\!$ is known to join ![]() $p_0^\pm$ and it represents the Bohm's metric. The graphs indicate that
$p_0^\pm$ and it represents the Bohm's metric. The graphs indicate that ![]() $\gamma _{s_1}$ converges to
$\gamma _{s_1}$ converges to ![]() $q_1^-$ for
$q_1^-$ for ![]() $s_1\in (0,s_\star )$ and converges to
$s_1\in (0,s_\star )$ and converges to ![]() $q_3^-$ for
$q_3^-$ for ![]() $s_1\in (s_{\star },\infty )$. (a)
$s_1\in (s_{\star },\infty )$. (a) ![]() $\gamma _{s_1}$ for
$\gamma _{s_1}$ for ![]() $m=1$. (b)
$m=1$. (b) ![]() $s_1\in (0,s_\star )$. (c)
$s_1\in (0,s_\star )$. (c) ![]() $s_2\in (s_\star,\infty )$.
$s_2\in (s_\star,\infty )$.

Figure A.2. Theorems 1.1 and 1.2 claim that for ![]() $m\geq 2$ there are at least two integral curves
$m\geq 2$ there are at least two integral curves ![]() $\gamma _{s_\star }$ and
$\gamma _{s_\star }$ and ![]() $\gamma _{s_{\star \star }}$ that join
$\gamma _{s_{\star \star }}$ that join ![]() $p_0^\pm$. The graphs indicate that
$p_0^\pm$. The graphs indicate that ![]() $\gamma _{s_1}$ converges to
$\gamma _{s_1}$ converges to ![]() $q_1^-$ for
$q_1^-$ for ![]() $s_1\in (0,s_\star )\cup (s_{\star \star },\infty )$ and converges to
$s_1\in (0,s_\star )\cup (s_{\star \star },\infty )$ and converges to ![]() $q_2^-$ for
$q_2^-$ for ![]() $s_1\in (s_{\star },s_{\star \star })$. (a)
$s_1\in (s_{\star },s_{\star \star })$. (a) ![]() $\gamma _{s_1}$ for
$\gamma _{s_1}$ for ![]() $m=2$. (b)
$m=2$. (b) ![]() $s_1\in (0,s_\star )$. (c)
$s_1\in (0,s_\star )$. (c) ![]() $s_2\in (s_\star,s_{\star \star })$. (d)
$s_2\in (s_\star,s_{\star \star })$. (d) ![]() $s_2\in (s_{\star \star },\infty )$.
$s_2\in (s_{\star \star },\infty )$.

Figure A.3. These plots are a realization of Theorem 1.3. For ![]() $m=1$, the graph of
$m=1$, the graph of ![]() $\zeta _0$ is the straight line that joins
$\zeta _0$ is the straight line that joins ![]() $p_1^\pm$. As
$p_1^\pm$. As ![]() $s_2$ increases from
$s_2$ increases from ![]() $0$, the integral curve
$0$, the integral curve ![]() $\zeta _{s_2}$ converges to
$\zeta _{s_2}$ converges to ![]() $q_1^-$, until
$q_1^-$, until ![]() $\zeta _{ {1}/({2m+6})}$ converges to
$\zeta _{ {1}/({2m+6})}$ converges to ![]() $p_0^-$. For
$p_0^-$. For ![]() $s_2> {1}/({2m+6})$, the integral curve
$s_2> {1}/({2m+6})$, the integral curve ![]() $\zeta _{s_2}$ converges to
$\zeta _{s_2}$ converges to ![]() $q_3^-$, until
$q_3^-$, until ![]() $s_2=s_\bullet$ once again joins
$s_2=s_\bullet$ once again joins ![]() $p_1^\pm$. For the
$p_1^\pm$. For the ![]() $s_2>s_\bullet$, the integral curve
$s_2>s_\bullet$, the integral curve ![]() $\zeta _{s_2}$ converges again to
$\zeta _{s_2}$ converges again to ![]() $q_1^-$. (a)
$q_1^-$. (a) ![]() $\zeta _{s_2}$ for
$\zeta _{s_2}$ for ![]() $m=1$. (b)
$m=1$. (b) ![]() $s_2\in (0, {1}/({2m+6}))$. (c)
$s_2\in (0, {1}/({2m+6}))$. (c) ![]() $s_2\in ( {1}/({2m+6}),s_\bullet )$. (d)
$s_2\in ( {1}/({2m+6}),s_\bullet )$. (d) ![]() $s_2\in (s_\bullet,\infty )$.
$s_2\in (s_\bullet,\infty )$.

Figure A.4. For ![]() $m\geq 2$, the behavior of
$m\geq 2$, the behavior of ![]() $\zeta _{s_2}$ is relatively simpler. For
$\zeta _{s_2}$ is relatively simpler. For ![]() $s_2\in (0, {1}/({2m+6}))$, the integral curve
$s_2\in (0, {1}/({2m+6}))$, the integral curve ![]() $\zeta _{s_2}$ converges to
$\zeta _{s_2}$ converges to ![]() $q_1^-$. For
$q_1^-$. For ![]() $s_2> {1}/({2m+6})$, the integral curve
$s_2> {1}/({2m+6})$, the integral curve ![]() $\zeta _{s_2}$ converges to
$\zeta _{s_2}$ converges to ![]() $q_2^-$. (a)
$q_2^-$. (a) ![]() $\zeta _{s_2}$ for
$\zeta _{s_2}$ for ![]() $m=1$. (b)
$m=1$. (b) ![]() $s_2\in (0, {1}/({2m+6}))$. (c)
$s_2\in (0, {1}/({2m+6}))$. (c) ![]() $s_2\in ( {1}/({2m+6}),\infty )$.
$s_2\in ( {1}/({2m+6}),\infty )$.
A.3 Visual summaries
We summarize Theorem 1.1–1.3 in Figures A.1–A.4 generated by Grapher, where integral curves presented are generated by the fourth-order Runge–Kutta algorithm with step size 0.01 and the initial step is set in a neighborhood around ![]() $p_0^+$ or
$p_0^+$ or ![]() $p_1^+$. All figures are in the
$p_1^+$. All figures are in the ![]() $X_1X_2Z$-space and the variable
$X_1X_2Z$-space and the variable ![]() $Y$ is eliminated by (2.8).
$Y$ is eliminated by (2.8).
Acknowledgements
I am grateful to McKenzie Wang for his constant support and encouragement. I am also thankful to Christoph Böhm for his helpful suggestions and remarks on this project. I would like to thank Cheng Yang and Wei Yuan for many inspiring discussions. I thank the referees for finding errors and typos, and for making suggestions that improve the quality of this paper.
Conflicts of Interest
None.