In this paper we prove that a pure, regular, totally odd, polarizable weakly compatible system of 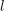$l$-adic representations is potentially automorphic. The innovation is that we make no irreducibility assumption, but we make a purity assumption instead. For compatible systems coming from geometry, purity is often easier to check than irreducibility. We use Katz’s theory of rigid local systems to construct many examples of motives to which our theorem applies. 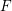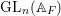We also show that if $F$ is a CM or totally real field and if ${\it\pi}$ is a polarizable, regular algebraic, cuspidal automorphic representation of $\text{GL}_{n}(\mathbb{A}_{F})$, then for a positive Dirichlet density set of rational primes 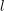$l$, the 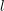$l$-adic representations 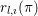$r_{l,\imath }({\it\pi})$ associated to ${\it\pi}$ are irreducible.

We study a subtle inequity in the distribution of unnormalized differences between imaginary parts of zeros of the Riemann zeta function, which was observed by a number of authors. We establish a precise measure which explains the phenomenon, that the location of each Riemann zero is encoded in the distribution of large Riemann zeros. We also extend these results to zeros of more general $L$-functions. In particular, we show how the rank of an elliptic curve over $\mathbb{Q}$ is encoded in the sequences of zeros of other$L$-functions, not only the one associated to the curve.

We prove the integral Tate conjecture for cycles of codimension $2$ on smooth cubic fourfolds over an algebraic closure of a field finitely generated over its prime subfield and of characteristic different from $2$ or $3$. The proof relies on the Tate conjecture with rational coefficients, proved in that setting by the first author, and on an argument of Voisin coming from complex geometry.

We prove a global Torelli theorem for pairs $(Y,D)$ where $Y$ is a smooth projective rational surface and $D\in |-K_{Y}|$ is a cycle of rational curves, as conjectured by Friedman in 1984. In addition, we construct natural universal families for such pairs.

We show the existence of a large family of representations supported by the orbit closure of the determinant. However, the validity of our result is based on the validity of the celebrated ‘Latin square conjecture’ due to Alon and Tarsi or, more precisely, on the validity of an equivalent ‘column Latin square conjecture’ due to Huang and Rota.

Thurston introduced shear deformations (cataclysms) on geodesic laminations–deformations including left and right displacements along geodesics. For hyperbolic surfaces with cusps, we consider shear deformations on disjoint unions of ideal geodesics. The length of a balanced weighted sum of ideal geodesics is defined and the Weil–Petersson (WP) duality of shears and the defined length is established. The Poisson bracket of a pair of balanced weight systems on a set of disjoint ideal geodesics is given in terms of an elementary $2$-form. The symplectic geometry of balanced weight systems on ideal geodesics is developed. Equality of the Fock shear coordinate algebra and the WP Poisson algebra is established. The formula for the WP Riemannian pairing of shears is also presented.

We extend to compact Kähler manifolds some classical results on linear representation of fundamental groups of complex projective manifolds. Our approach, based on an interversion lemma for fibrations with tori versus general type manifolds as fibers, gives a refinement of the classical work of Zuo. We extend to the Kähler case some general results on holomorphic convexity of coverings such as the linear Shafarevich conjecture.

We prove that, for simple modules $M$ and $N$ over a quantum affine algebra, their tensor product $M\otimes N$ has a simple head and a simple socle if $M\otimes M$ is simple. A similar result is proved for the convolution product of simple modules over quiver Hecke algebras.