Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T13:44:41.657Z Has data issue: false hasContentIssue false
  • English
  • Français

Simplicity of heads and socles of tensor products

Part of: Groups and algebras in quantum theory Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  26 November 2014

Seok-Jin Kang ,
Masaki Kashiwara ,
Myungho Kim  and
Se-jin Oh
Seok-Jin Kang
Affiliation:
Department of Mathematical Sciences and Research Institute of Mathematics, Seoul National University, Seoul 151-747, Korea email [email protected]
Masaki Kashiwara
Affiliation:
Research Institute for Mathematical Sciences, Kyoto University, Kyoto 606-8502, Japan Department of Mathematical Sciences and Research Institute of Mathematics, Seoul National University, Seoul 151-747, Korea email [email protected]
Myungho Kim
Affiliation:
School of Mathematics, Korea Institute for Advanced Study, Seoul 130-722, Korea email [email protected]
Se-jin Oh
Affiliation:
Department of Mathematical Sciences and Research Institute of Mathematics, Seoul National University, Seoul 151-747, Korea email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

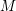We prove that, for simple modules $M$ and 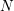$N$ over a quantum affine algebra, their tensor product 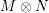$M\otimes N$ has a simple head and a simple socle if 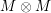$M\otimes M$ is simple. A similar result is proved for the convolution product of simple modules over quiver Hecke algebras.

Keywords

quantum affine algebraKhovanov–Lauda–Rouquier algebraR-matrix

MSC classification

Primary: 81R50: Quantum groups and related algebraic methods 17B37: Quantum groups (quantized enveloping algebras) and related deformations
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 2 , February 2015 , pp. 377 - 396
Copyright
© The Author(s) 2014 

References

Akasaka, T. and Kashiwara, M., Finite-dimensional representations of quantum affine algebras, Publ. Res. Inst. Math. Sci. (RIMS), Kyoto 33 (1997), 839–867.CrossRefGoogle Scholar
Ariki, S., On the decomposition numbers of the Hecke algebra of G (M, 1, n), J. Math. Kyoto Univ. 36 (1996), 789–808.Google Scholar
Berenstein, A. and Zelevinsky, A., String bases for quantum groups of type A r, in I. M. Gel’fand seminar, Advances in Soviet Mathematics, vol. 16 (American Mathematical Society, Providence, RI, 1993), 51–89.Google Scholar
Hernandez, D. and Leclerc, B., Cluster algebras and quantum affine algebras, Duke Math. J. 154 (2010), 265–341.CrossRefGoogle Scholar
Hernandez, D. and Leclerc, B., Quantum Grothendieck rings and derived Hall algebras, J. Reine Angew. Math., to appear; doi:10.1515/crelle-2013-0020.Google Scholar
Kac, V., Infinite dimensional Lie algebras, 3rd edition (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
Kang, S.-J., Kashiwara, M. and Kim, M., Symmetric quiver Hecke algebras and R-matrices of quantum affine algebras, Preprint (2013), arXiv:1304.0323v1.Google Scholar
Kang, S.-J., Kashiwara, M. and Kim, M., Symmetric quiver Hecke algebras and R-matrices of quantum affine algebras II, Duke Math. J., to appear, arXiv:1308.0651v1.Google Scholar
Kashiwara, M., On level zero representations of quantum affine algebras, Duke. Math. J. 112 (2002), 117–175.Google Scholar
Khovanov, M. and Lauda, A., A diagrammatic approach to categorification of quantum groups I, Represent. Theory 13 (2009), 309–347.Google Scholar
Khovanov, M. and Lauda, A., A diagrammatic approach to categorification of quantum groups II, Trans. Amer. Math. Soc. 363 (2011), 2685–2700.CrossRefGoogle Scholar
Lauda, A. and Vazirani, M., Crystals from categorified quantum groups, Adv. Math. 228 (2011), 803–861.Google Scholar
Leclerc, B., Imaginary vectors in the dual canonical basis of U q(n), Transform. Groups 8 (2003), 95–104.Google Scholar
Rouquier, R., 2-Kac-Moody algebras, Preprint (2008), arXiv:0812.5023v1.Google Scholar
Rouquier, R., Quiver Hecke algebras and 2-Lie algebras, Algebra Colloq. 19 (2012), 359–410.CrossRefGoogle Scholar
Varagnolo, M. and Vasserot, E., Canonical bases and KLR algebras, J. Reine Angew. Math. 659 (2011), 67–100.Google Scholar