Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-13T10:19:02.153Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphy and irreducibility of some l-adic representations

Part of: Algebraic number theory: global fields Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  24 October 2014

Stefan Patrikis  and
Richard Taylor
Stefan Patrikis
Affiliation:
Department of Mathematics, MIT, Building E18, 77 Massachusetts Avenue, Cambridge, MA 02139, USA email [email protected]
Richard Taylor
Affiliation:
School of Mathematics, Institute for Advanced Study, Einstein Drive, Princeton, NJ 08540, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

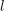In this paper we prove that a pure, regular, totally odd, polarizable weakly compatible system of $l$-adic representations is potentially automorphic. The innovation is that we make no irreducibility assumption, but we make a purity assumption instead. For compatible systems coming from geometry, purity is often easier to check than irreducibility. We use Katz’s theory of rigid local systems to construct many examples of motives to which our theorem applies. We also show that if 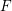$F$ is a CM or totally real field and if ${\it\pi}$ is a polarizable, regular algebraic, cuspidal automorphic representation of 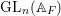$\text{GL}_{n}(\mathbb{A}_{F})$, then for a positive Dirichlet density set of rational primes 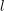$l$, the 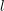$l$-adic representations 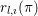$r_{l,\imath }({\it\pi})$ associated to ${\it\pi}$ are irreducible.

MSC classification

Primary: 11F80: Galois representations 11R39: Langlands-Weil conjectures, nonabelian class field theory
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 2 , February 2015 , pp. 207 - 229
Copyright
© The Author(s) 2014 

References

Abramovich, D. and Wang, J., Equivariant resolution of singularities in characteristic 0, Math. Res. Lett. 4(2–3) (1997), 427–433.Google Scholar
André, Y., Pour une théorie inconditionnelle des motifs, Publ. Math. Inst. Hautes Études Sci. 83 (1996), 5–49.CrossRefGoogle Scholar
Ash, A., Pinch, R. and Taylor, R., An A 4̂ extension of  ℚ attached to a non-selfdual automorphic form on GL(3), Math. Ann. 291 (1991), 753–766.Google Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Potential automorphy and change of weight, Ann. of Math. (2) 179 (2014), 501–609.Google Scholar
Beukers, F. and Heckman, G., Monodromy for the hypergeometric function nF n−1, Invent. Math. 95 (1989), 325–354.Google Scholar
Caraiani, A., Monodromy and local-global compatibility for $l=p$, Algebra Number Theory, to appear, Preprint (2012), arXiv:1202.4683.Google Scholar
Cattani, E., Kaplan, A. and Schmid, W., Degeneration of Hodge structures, Ann. of Math. (2) 123 (1986), 457–535.Google Scholar
Clozel, L., Motifs et formes automorphes: applications du principe de fonctorialité, in Automorphic forms, Shimura varieties, and L-functions I, Perspectives in Mathematics, vol. 10 (Academic Press, New York, 1990).Google Scholar
Deligne, P., Théorie de Hodge. I., in Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 1 (Gauthier-Villars, Paris, 1971), 425–430.Google Scholar
Deligne, P., La conjecture de Weil. I., Publ. Math. Inst. Hautes Études Sci. 43 (1974), 273–307.Google Scholar
Deligne, P., Un théorème de finitude pour la monodromie, in Discrete groups in geometry and analysis, Progress in Mathematics, vol. 67 (Birkhäuser, Boston, MA, 1987).Google Scholar
Dettweiler, M. and Reiter, S., Rigid local systems and motives of type G 2, Compositio Math. 146 (2010), 929–963.Google Scholar
Dettweiler, M. and Sabbah, C., Hodge theory of the middle convolution, Publ. Res. Inst. Math. Sci. 49 (2013), 761–800.Google Scholar
Harris, M., Shepherd-Barron, N. and Taylor, R., A family of Calabi–Yau varieties and potential automorphy, Ann. of Math. (2) 171 (2010), 779–813.Google Scholar
Katz, N., Rigid local systems, Annals of Mathematics Studies, vol. 139 (Princeton University Press, Princeton, NJ, 1996).Google Scholar
Patrikis, S., Variations on a theorem of Tate, Preprint (2014), arXiv:1207.6724v4.Google Scholar
Pink, R., On the calculation of local terms in the Lefschetz Verdier trace formula and its application to a conjecture of Deligne, Ann. of Math. (2) 135 (1992), 483–525.Google Scholar
Schmid, W., Variation of Hodge structure: the singularities of the period mapping, Invent. Math. 22 (1973), 211–319.CrossRefGoogle Scholar
Taylor, R., The image of complex conjugation in l-adic representations associated to automorphic forms, Algebra Number Theory 6 (2012), 405–435.CrossRefGoogle Scholar